强化学习(英语:Reinforcement learning,简称RL)是机器学习中的一个领域,**强调如何基于环境而行动,以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论,即有机体如何在环境给予的奖励或惩罚的刺激下,逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。**这个方法具有普适性,因此在其他许多领域都有研究,例如博弈论、控制论、运筹学、信息论、仿真优化、多主体系统学习、群体智能、统计学以及遗传算法。在运筹学和控制理论研究的语境下,强化学习被称作“近似动态规划”(approximate dynamic programming,ADP)。在最优控制理论中也有研究这个问题,虽然大部分的研究是关于最优解的存在和特性,并非是学习或者近似方面。在经济学和博弈论中,强化学习被用来解释在有限理性的条件下如何出现平衡。
在机器学习问题中,环境通常被规范为马可夫决策过程(MDP),所以许多强化学习算法在这种情况下使用动态规划技巧。传统的技术和强化学习算法的主要区别是,后者不需要关于MDP的知识,而且针对无法找到确切方法的大规模MDP。
强化学习和标准的监督式学习之间的区别在于,它并不需要出现正确的输入/输出对,也不需要精确校正次优化的行为。强化学习更加专注于在线规划,需要在探索(在未知的领域)和遵从(现有知识)之间找到平衡。强化学习中的“探索-遵从”的交换,在多臂老虎机问题和有限MDP中研究得最多。 -----------(来自维基百科)
以上述多臂老虎机为例,我们假设有10台机器,每台机器的奖励分布情况不同。进行10000次游戏,如何选择机器才能达到最大收益?
为了简化问题,我们把奖励大于我们一次游戏投入,(即收益)记为得分1,否则记为0。(可能不是很恰当,不过作为说明的例子应该没问题)
为了训练,当然需要一个数据集,这里假设我们有一个模拟数据集(10000 * 10)。大致如下:

解释下这个模拟数据集如何看:假设我们进行了第一次游戏,即第0行,如果我们选择了机器编号为1,5,9则得分1,其他得分0,依次类推…
如果我们进行了随机选择,看下收益情况还有10000此游戏中每个机器选择的次数:
import pandas as pd
import numpy as np
dataset = pd.read_csv('Machine.csv')
import random
machine_selected = [] #用于存储每一轮游戏选择的机器。
final_score = 0 #用于存储第n轮之前的总得分。
for n in range(10000):
machine_num = random.randrange(10)
machine_selected.append(machine_num)
score = dataset.values[n,machine_num]
finnal_reword = finnal_score + score
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.hist(machine_selected)
plt.xticks(np.arange(10),[1,2,3,4,5,6,7,8,9,10])
plt.xlabel('机器编号')
plt.ylabel('选择次数')
plt.show()
输出:
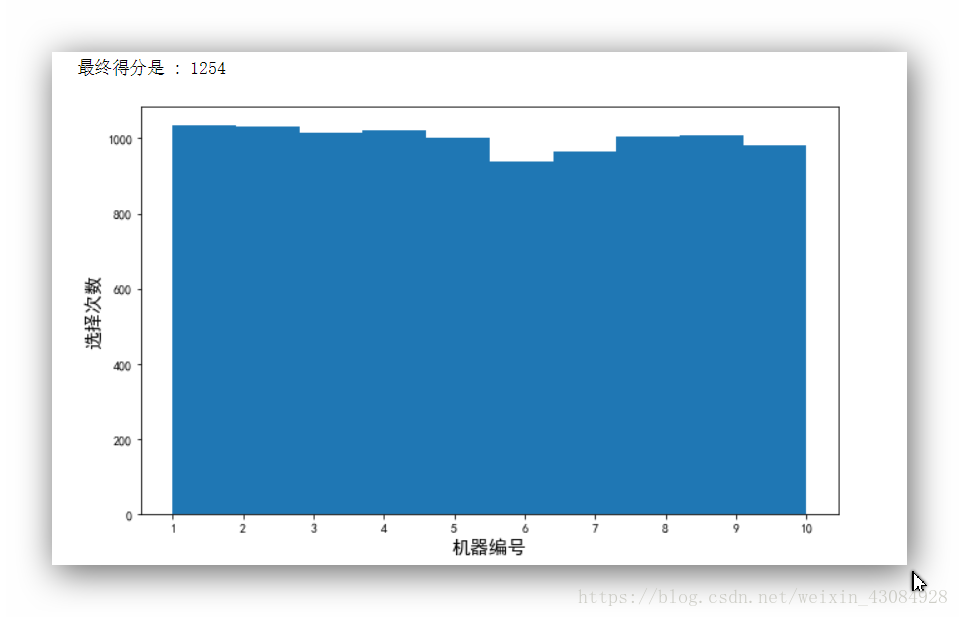
可以看到,最终我们的收益是1254,各个机器的选择次数也很平均,很符合我们的随机结果。
接下来看下强化学习的置信区间算法的结果:
import pandas as pd
import numpy as np
import math
dataset = pd.read_csv('Machine.csv')
number_of_selected = [0] * 10 #初始化每个机器的选择次数
sum_score = [0] * 10 #初始化每个机器的得分
machine_selected = [] #记录10000次游戏的每一次机器选择
total_score = 0 #初始化总得分
'''
这里需要解释下下面的代码。对于每一个机器的第一次选择,由于我们还未进行探索,所以需要先遍历每个机器一次。
实现如下,先设置一个很大的置信区上界(max_UB),这里是10的300次方。
对于每个机器的第一次运行,我们进行赋值UB= 1e300从而运行了每一台机器,
我们的条件UB>max_UB不成立,machine = 0,也就是第一台机器,而后我们有了对每台机器的第一次探索信息
接下来的遍历,每个number_of_selected[i] > 0都是成立的,因此进入该条件下的代码,每次选择了机器,
计算该机器的置信区间上界,比较与其他几个机器的上界,选出最高的那个进行新一轮游戏。
'''
for n in range(0,10000):
machine = 0
max_UB = 0
for i in range(0,10):
if number_of_selected[i] > 0:
average = sum_score[i] / number_of_selected[i]
delta = math.sqrt(3 / 2 * math.log(n+1) / number_of_selected[i])
UB = average + delta
else:
UB = 1e300
if UB > max_UB:
max_UB = UB
machine = i
machine_selected.append(machine)
score = dataset.values[n,machine] #根据模拟数据,索引得到得分值。
number_of_selected[machine] = number_of_selected[machine] + 1
sum_score[machine] = sum_score[machine] + score
total_score = total_score + score
print('最终得分是 : ' + str(total_score))
import matplotlib.pyplot as plt
plt.figure(figsize= (10,6))
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.hist(machine_selected)
plt.xticks(np.arange(10),[1,2,3,4,5,6,7,8,9,10])
plt.title('置信区间上界算法的结果',fontsize = 20)
plt.xlabel('机器编号',fontsize = 15)
plt.ylabel('选择次数',fontsize = 15)
plt.show()
输出:
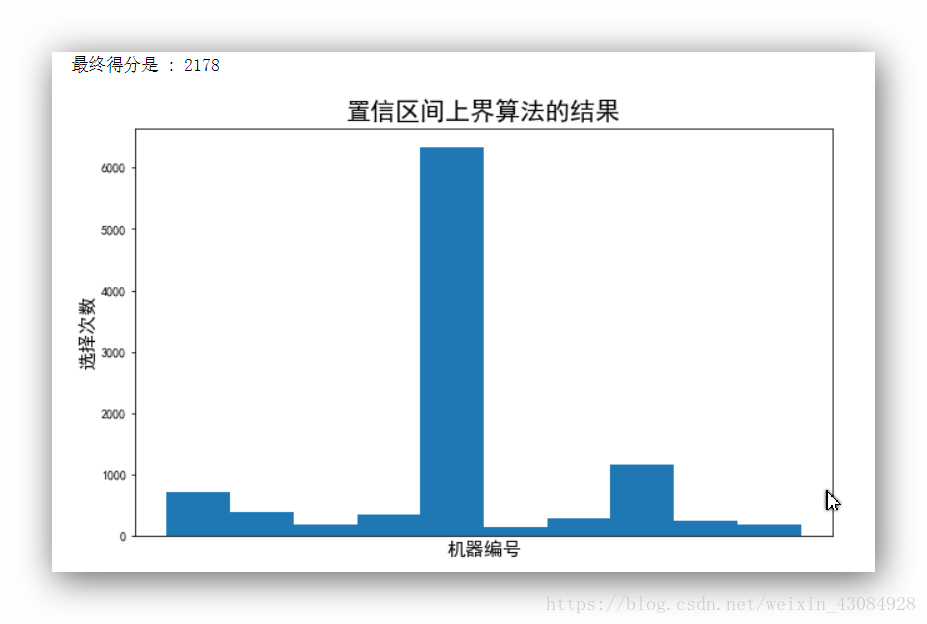
可以看到相比随机进行游戏,我们的收益提升还是非常明显的,总得分是2178,同时可以看到5号机器被选择的次数最多,从中可以得知,5号机器相比其它几个机器对玩家还是挺友好的…
后续会视情况可能会写篇文章大致介绍下置信区间上界算法的过程。
最后
以上就是干净皮带最近收集整理的关于初探强化学习:置信区上界解决多臂老虎机问题的全部内容,更多相关初探强化学习内容请搜索靠谱客的其他文章。








发表评论 取消回复