Machine Learning A-Z学习笔记15-置信区间算法

1.简单原理

用多臂老虎机问题，也就是探讨如何用最少的代价得知哪一台老虎机的中奖率最高，作为置信区间算法(Upper Confidence Bound, UCB)的举例。

这张图是五台老虎机的中奖概率分布，X轴代表奖金额度，Y轴代表中概率，所以我们可以知道第五台老虎机的报酬率最高。接下来要探讨如何用一个良好的策略，通过不断的"探索(exploration)"，尽快找到拥有最佳中奖概率分布的老虎机，并且"利用(exploitation)"这台老虎机最大化我们的奖励.探索和利用这两步实际上并不是那么的兼容，为了解释这个概念，这里引入一个定义，叫做遗憾。也就是我们知道D5的分布是最高的，那么最佳策略是应对不停的选择D5这个机器，但当我们不知道的时候，可能会选择其他的机器，当没有选择最佳机器时，都会得到一个得到的奖励和最佳奖励的差，这个差就是遗憾。

那么现在可以解释为什么探索和利用为什么并不是那么兼容，比如我们探索很多，每个机器玩了一百次，对于每个机器都能得到很好的分布估计，但同时也会带来很多的遗憾。如果探索比较少，可能会找不到最佳的分布，探索得到的结论可能是错的。所以说，最佳的策略应该是，通过探索找到最佳分布的老虎机，并且以一种快速而高效的方法找到这个老虎机，且不断的利用它来获得最大化的奖励。

下面来描述下这个算法,现在假设我们知道五台老虎机的分布，那么我们会不断的选择D5这个老虎机。假如说不知道这几个的概率分布，那么就要开始我们的算法。

第一步，在我们开始之前，假设每个老虎机的概率分布是相同的，即平均值或期望是相同的。如图红色虚线表示平均值或期望，纵轴表示老虎机可能带来的收益。这些彩色的横线代表每个老虎机实际的平均或期望，这些期望我们是不知道的，这个问题的核心就是我们要进行不断的尝试去估算出每个老虎机的平均期望。

那么此时第三个机器的置信区间上界比其他的要低，所以下一轮要选择其他四个机器，比如选择第四个，那么它的置信区间上界会变高，区间大小会变小。

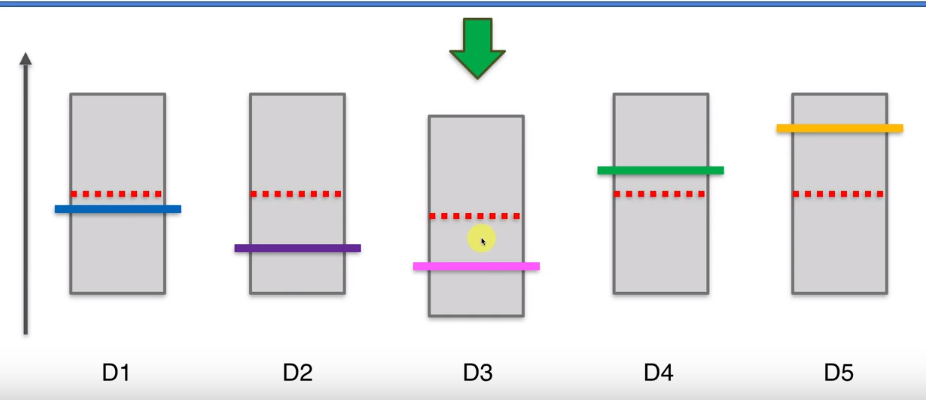
在下一步，125三个机器的上界时一样的，因此可以在他们三个中间选一个，比如第一个，它的实际平均值比较低，但当我们按下老虎机的时候，它实际是个随机事件，因此可能高也可能低。虽然它的平均值，但假设此时运气比较好，投下去的钱翻倍了，那么他的区间上限变高，长度变小。

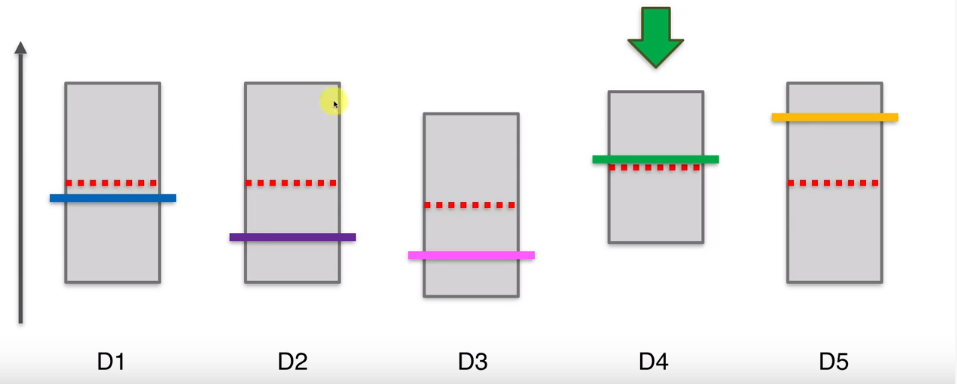
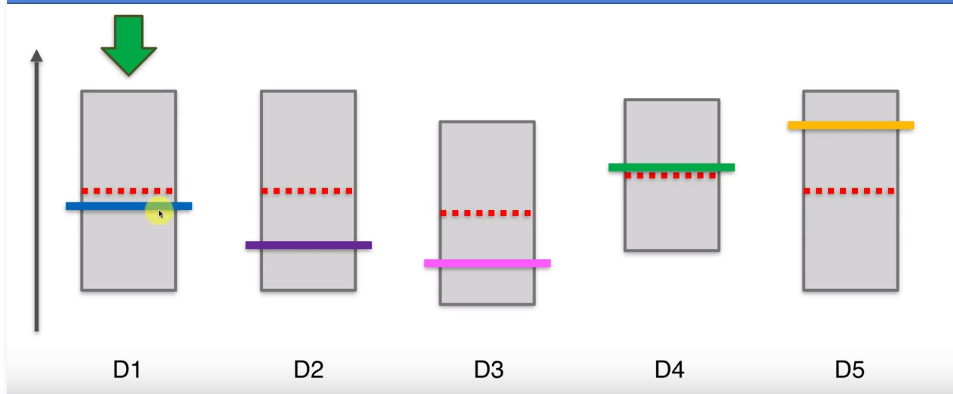
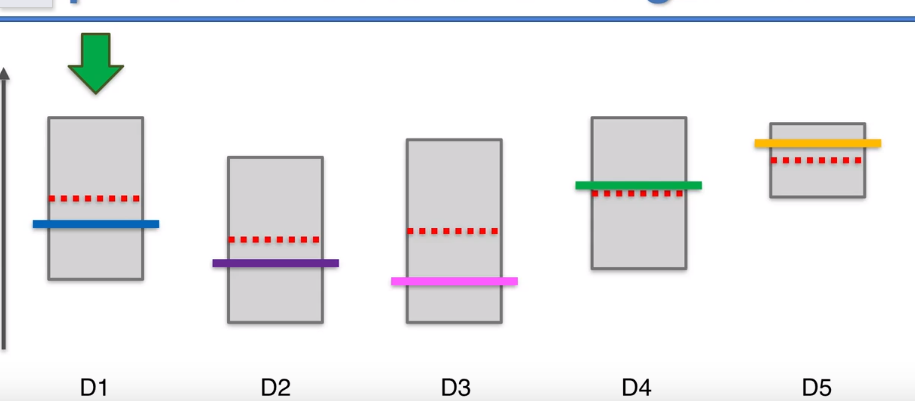
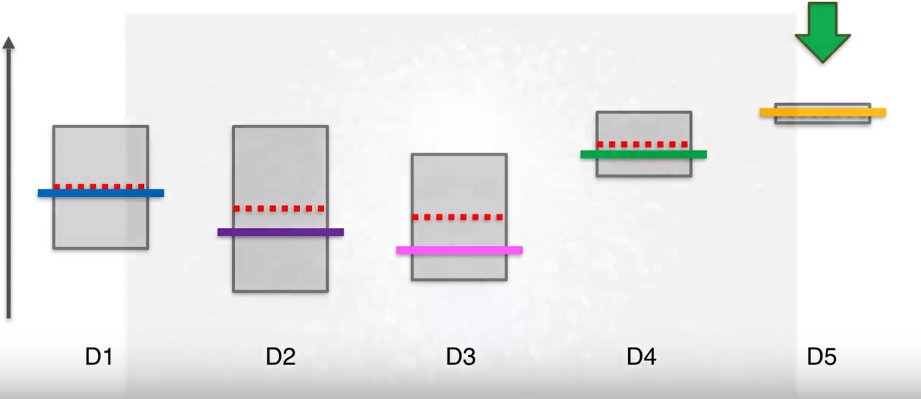
UCB算法有一个特点，当我们选择了一个机器很多次后，他的置信区间会变得很小，要给其他的机器一些机会，看看其他机器显示的观察结果所对应的新的置信区间上界是否会更高。这样经过很多轮后，最终D5的选择次数依然会很多很多，他的置信区间会越来越扁，一直到最终轮。

2.相关代码

# Upper Confidence Bound
"""
在广告播放过程中，根据广告的即时欢迎程度(点击率)回馈资讯，用UCB调整播放内容


"""

# Importing the libraries
"""
导入库
"""
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
"""
数据导入
"""
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')

# Implementing UCB
"""
建立UCB，每回合只投1个广告给1个用户
-N = 10000:投10000次广告，也可以说是1万个用户
-d = 10:广告长度
-ads_selected = []:纪录器，记录每轮推播哪个广告。其长度等于推播数(回合数)，并且等于N
-numbers_of_selections = [0] * d:每个广告总共被选择几次
-sums_of_rewards = [0] * d:每个广告的总得分数
-total_reward = 0:所有广告的得分数总和
"""
import math
N = 10000
d = 10
ads_selected = []
numbers_of_selections = [0] * d#一个10位为0的数组
sums_of_rewards = [0] * d
total_reward = 0
for n in range(0, N):
    ad = 0
    max_upper_bound = 0
    
    # Step 1. 对每个广告作的平均期望值与置信区间更新
    for i in range(0, d):
        if (numbers_of_selections[i] > 0):
            
            # Step 2. 广告i的平均期望值变量计算
            average_reward = sums_of_rewards[i] / numbers_of_selections[i]
            delta_i = math.sqrt(3/2 * math.log(n + 1) / numbers_of_selections[i])
            
            # Step 3 广告i的平均期望值更新
            upper_bound = average_reward + delta_i
        else:
            #一开始(第一轮)每个广告的置信区间很大
            upper_bound = 1e400
        
        # 更新下一轮要推播的广告以及目前最高的天花板(UCB)
        if upper_bound > max_upper_bound:
            max_upper_bound = upper_bound
            ad = i
    
    #更新纪录器
    ads_selected.append(ad)
    
    #广告i被点击数+1
    numbers_of_selections[ad] = numbers_of_selections[ad] + 1
    
    #从数据库得知本轮用户是否有观看本次推播的广告i，若有则1、若否则0
    reward = dataset.values[n, ad]
    
    #广告i得分数更新
    sums_of_rewards[ad] = sums_of_rewards[ad] + reward
    
    #所有广告总得分树更新
    total_reward = total_reward + reward

# Visualising the results
"""
结果可视化
"""
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()
# Random Selection
"""
模拟实际情境用
-随机挑选广告给每一用户，然后再根据Ads_CTR_Optimisation.csv的结果作比较(符合得10分)
最后得到total_reward，因为是随机抽取逛告进行推播，所以10个广告的得分会差不多

"""
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')

# Implementing Random Selection
import random
N = 10000
d = 10
ads_selected = []
total_reward = 0
for n in range(0, N):
    ad = random.randrange(d)
    ads_selected.append(ad)
    reward = dataset.values[n, ad]
    total_reward = total_reward + reward

# Visualising the results
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()

最后

以上就是健忘保温杯为你收集整理的Machine Learning A-Z学习笔记15-置信区间算法Machine Learning A-Z学习笔记15-置信区间算法的全部内容，希望文章能够帮你解决Machine Learning A-Z学习笔记15-置信区间算法Machine Learning A-Z学习笔记15-置信区间算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。