一文快速搞懂对95%置信区间的理解

综合知乎上各大神的解答和网络资料得到本文对95%置信区间的理解

先给出结论

• 最常出现的对置信区间的错误理解：

在95%置信区间内，有95%的概率包括真实参数  （错误！！）

在95%置信区下构建的模型，意味着模型参数对于试图近似的函数有95%的概率是真实值的估计值（错误！！）

• 正确解释应为：

95%置信区间，意味着如果你用同样的步骤，去选样本，计算置信区间，那么100次这样的独立过程，有95%的概率你计算出来的区间会包含真实参数值，即大概会有95个置信区间会包含真值。

而对于某一次计算得到的某一个置信区间，其包含真值的概率，我们无法讨论。

我们平常使用的频率学派（frequentist）95% 置信区间的意思并不是真值在这个区间内的概率是 95%。真值要么在，要么不在。由于在频率学派当中，真值是一个常数，而非随机变量（后者是贝叶斯学派） ，所以我们不对真值做概率描述。对于这个问题来说，理解的关键是我们是对这个构造置信区间的方法做概率描述，而非真值，也非我们算得的这个区间本身。

换言之，我们可以说，如果我们重复取样，每次取样后都用这个方法构造置信区间，有 95% 的置信区间会包含真值 。然而（在频率学派当中）我们无法讨论其中某一个置信区间包含真值的概率。

参考自：如何理解 95% 置信区间？ - 管致远的回答 - 知乎  https://www.zhihu.com/question/26419030/answer/70589735

详细一点的分析

截图参考来源：知乎-如何理解 95% 置信区间？

- 马同学的回答 - 知乎 https://www.zhihu.com/question/26419030/answer/274472266
著作权归作者所有

估计又分为“点估计”和“区间估计”

而区间估计又称为置信区间估计，要得到一个置信区间需要样本统计量（比如均值）和从数据中计算出方差，中心极限定理告诉我们均值会接近一个高斯分布，我们可以用标准差计算出真实期望落在选定区间的概率，例如，以均值μ^为中心的概率为0.95的区域为（基于高斯分布）：

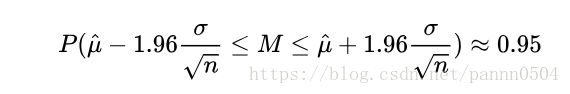
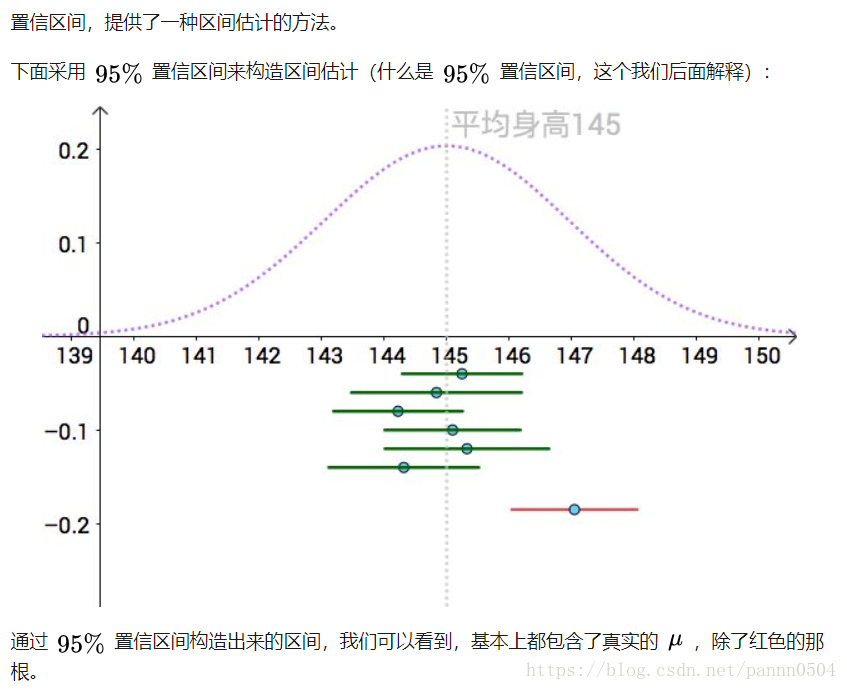
题外话：在机器学习实验中，我们通常用测试集样本的误差均值来估计泛化误差，一般我们说算法A比算法B好，是指算法A的误差的95%置信区间的上界小于算法A的误差的95%置信区间的下界。

总结来说

转自邸月宝科学网博客
链接地址：http://blog.sciencenet.cn/blog-925634-870778.html 

假设现在是95%的置信水平（ 95%也被称为置信水平，是统计中的一个习惯，可以根据应用进行调整），每个从总体中抽出的样本都可以求出一个95%的置信区间，且不同样本求出的置信区间是不同的，但随着抽出的样本次数的增加，例如抽100次，得到100个样本，每个样本都对应一个置信区间，那么100次抽样求出的100个置信区间有95个包含真实的总体均值。

置信区间会因样本的不同而不同（置信区间是怎么算的？是通过样本（sample）算的），而且不是所有的区间都包含真值，一个区间就像是一个为了捕获总体未知参数而撒出的网，不是所有撒网的地点都能捕获我们想要的总体的参数。

最后

以上就是欣慰微笑为你收集整理的一文快速搞懂对95%置信区间的理解一文快速搞懂对95%置信区间的理解的全部内容，希望文章能够帮你解决一文快速搞懂对95%置信区间的理解一文快速搞懂对95%置信区间的理解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。