强化学习中的两种探索-平衡策略
- ε-greedy方法
- UCB(Upper Confidence Bound)方法
为了解决强化学习中的一个经典问题:exploration and exploitation tradeoff 即:到底我们应该花精力去探索从而对收益有更精确的估计,还是应该按照目前拥有的信息,选择最大收益期望的行为?
这样看上去可能不好理解,一个小例子帮助理解:
假如你想在淘宝上买一本书,你一输入书的名字就看到,第一个链接的价格为10元,第二个链接为9.9元,第三个为11元,此时你有两个选择,直接买9.9元的书,因为这是你目前看到最便宜的价格。这就是exploitation。但是现实中你并不会这么做,至少大部分人不会这么做,大家应该都会继续把列表往下翻,你有可能还会找到8元的价格,这个价格显然更加划算,但你付出了更多的时间精力。这就是exploration。 更多的exploration可能会得到更多的收益,但会花费更大的精力,直接exploitation虽然节省精力,但不一定得到更多的收益,这样就会存在exploration 和 exploitation 的平衡问题。
ε-greedy和UCB就是exploration and exploitation tradeoff中两种常用的策略。
1.ε-greedy方法
a = { a r g m a x q ( a ) , 1 − ε 随 机 , ε a=begin{cases} argmaxq(a) ,& 1-ε \ 随机, & ε end{cases} a={argmaxq(a),随机,1−εε
以1-ε 的概率选择q值大的动作,以ε的概率选择随机动作
例子:
| a1 | a2 | a3 | |
|---|---|---|---|
| 当前时刻 | q(a1)=0.2 | q(a2)=0.3 | q(a3)=0.6 |
| 下一时刻 | q(a1)=0.2 | q(a2)=1.5 | q(a3)=0.3 |
如果我们根据贪婪策略的话,会选择q值大的那个动作,即a3。但下一时刻q值就会变化,因此根据贪婪策略我们的最终收益只会是0.6+0.3=0.9。
但根据ε-greedy方法,当前时刻也有ε的概率选择到动作a2,最终的收益为0.3+1.5=1.8,显然最终的收益比贪婪策略得到的要高。
代码实现:
def choose_action(self, policy, **kwargs):
if np.random.random() < kwargs['epsilon']:
action = np.random.randint(1, 4)
else:
action = np.argmax(self.q) + 1
return action
2.UCB方法
在ε-greedy方法收敛后,仍然会以一个ε的概率去选择不是最优的动作,容易造成精力的白白浪费。
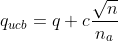
该公式分为两部分,前半部分是正在的q值,可以理解为exploitation。后半部分可视为影响因子,n为总的动作数,该部分随着动作a的选择次数增加而减小,从而更偏向于探索执行次数少的动作,可理解为exploration。
ε-greedy方法也可以设置衰减因子,让ε随着循环次数的增加而衰减,最终衰减到很小的值,此时ε-greedy方法也就变成了贪婪算法。此方法也能让ε-greedy方法达到和UCB差不多的效率。
代码实现:
def choose_action(self, policy, **kwargs):
c_ratio = kwargs['c_ratio']
if 0 in self.action_counts:
action = np.where(self.action_counts==0)[0][0]+1
else:
value = self.q + c_ratio*np.sqrt(np.log(self.counts) / self.action_counts)
action = np.argmax(value)+1
return action
3.总结
为了比较两种方法的优劣,将两种方法放在一个多臂赌博机的例子中进行对比,代码如下:
import numpy as np
import matplotlib.pyplot as plt
class KB_Game:
def __init__(self, *args, **kwargs):
self.q = np.array([0.0, 0.0, 0.0])
self.action_counts = np.array([0,0,0])
self.current_cumulative_rewards = 0.0
self.actions = [1, 2, 3]
self.counts = 0
self.counts_history = []
self.cumulative_rewards_history=[]
self.a = 1
self.reward = 0
def step(self, a):
r = 0
if a == 1:
r = np.random.normal(1,1)
if a == 2:
r = np.random.normal(2,1)
if a == 3:
r = np.random.normal(1.5,1)
return r
def choose_action(self, policy, **kwargs):
action = 0
if policy == 'e_greedy':
if np.random.random()<kwargs['epsilon']:
action = np.random.randint(1,4)
else:
action = np.argmax(self.q)+1
if policy == 'ucb':
c_ratio = kwargs['c_ratio']
if 0 in self.action_counts:
action = np.where(self.action_counts==0)[0][0]+1
else:
value = self.q + c_ratio*np.sqrt(np.log(self.counts) / self.action_counts)
action = np.argmax(value)+1
if policy == 'boltzmann':
tau = kwargs['temperature']
p = np.exp(self.q/tau)/(np.sum(np.exp(self.q/tau)))
action = np.random.choice([1,2,3], p = p.ravel())
return action
def train(self, play_total, policy, **kwargs):
reward_1 = []
reward_2 = []
reward_3 = []
for i in range(play_total):
action = 0
if policy == 'e_greedy':
action = self.choose_action(policy,epsilon=kwargs['epsilon'] )
if policy == 'ucb':
action = self.choose_action(policy, c_ratio=kwargs['c_ratio'])
if policy == 'boltzmann':
action = self.choose_action(policy, temperature=kwargs['temperature'])
self.a = action
# print(self.a)
#与环境交互一次
self.r = self.step(self.a)
self.counts += 1
#更新值函数
self.q[self.a-1] = (self.q[self.a-1]*self.action_counts[self.a-1]+self.r)/(self.action_counts[self.a-1]+1)
self.action_counts[self.a-1] +=1
reward_1.append([self.q[0]])
reward_2.append([self.q[1]])
reward_3.append([self.q[2]])
self.current_cumulative_rewards += self.r
# self.cumulative_rewards_history.append(self.current_cumulative_rewards)
self.cumulative_rewards_history.append(self.current_cumulative_rewards / self.counts) # 平均奖励
self.counts_history.append(i)
# self.action_history.append(self.a)
# plt.figure(1)
# plt.plot(self.counts_history, reward_1,'r')
# plt.plot(self.counts_history, reward_2,'g')
# plt.plot(self.counts_history, reward_3,'b')
# plt.draw()
# plt.figure(2)
# plt.plot(self.counts_history, self.cumulative_rewards_history,'k')
# plt.draw()
# plt.show()
def reset(self):
self.q = np.array([0.0, 0.0, 0.0])
self.action_counts = np.array([0, 0, 0])
self.current_cumulative_rewards = 0.0
self.counts = 0
self.counts_history = []
self.cumulative_rewards_history = []
self.a = 1
self.reward = 0
def plot(self, colors, policy,style):
plt.figure(1)
plt.plot(self.counts_history,self.cumulative_rewards_history,colors,label=policy,linestyle=style)
plt.legend()
plt.xlabel('n',fontsize=18)
plt.ylabel('total rewards',fontsize=18)
# plt.figure(2)
# plt.plot(self.counts_history, self.action_history, colors, label=policy)
# plt.legend()
# plt.xlabel('n', fontsize=18)
# plt.ylabel('action', fontsize=18)
if __name__ == '__main__':
np.random.seed(0)
k_gamble = KB_Game()
total = 2000
k_gamble.train(play_total=total, policy='e_greedy', epsilon=0.05)
k_gamble.plot(colors='r',policy='e_greedy',style='-.')
k_gamble.reset()
# k_gamble.train(play_total=total, policy='boltzmann',temperature=1)
# k_gamble.plot(colors='b', policy='boltzmann',style='--')
# k_gamble.reset()
k_gamble.train(play_total=total, policy='ucb', c_ratio=0.5)
k_gamble.plot(colors='g', policy='ucb',style='-')
plt.show()
# k_gamble.plot(colors='r', strategy='e_greedy')
# k_gamble.reset()
# k_gamble.train(steps=200, strategy='ucb', c_ratio=0.5)
# k_gamble.plot(colors='g', strategy='ucb')
# k_gamble.reset()
# k_gamble.train(steps=200, strategy='boltzmann', a_ratio=0.1)
# k_gamble.plot(colors='b', strategy='boltzmann')
# plt.show()
代码运行结果如下:
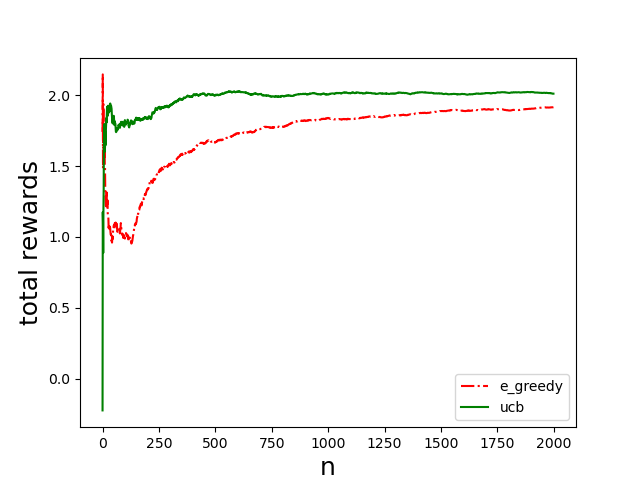
从图中可以看出,UCB算法能更快达到最大收益,且更加稳定。UCB的累计收益也要高于ε-greedy。
最后
以上就是尊敬大侠最近收集整理的关于强化学习中的两种探索-平衡策略强化学习中的两种探索-平衡策略的全部内容,更多相关强化学习中内容请搜索靠谱客的其他文章。








发表评论 取消回复