openGL学习过程（2）Bresenham算法画线和圆以及三角形的光栅化

1. 使用Bresenham算法(只使用integer arithmetic)画一个三角形边框

算法的主要思想就是当前一个点确定的时候，这时候下一个点由于一定要在格点地上，所以只会有两种选择，（下图是当斜率小于1且方向为正向的情况），要么是（x+1，y）的点，要么是(x+1,y+1)的点，然后直线上真实的点应该是（x+1, m(x+1)+b），这时候就看这个真实点距离哪个格点比较近就行了。

两个距离的计算公式如下：

又由于我们只需要知道哪个大，就直接求差看正负符号

M是斜率，要用到除法，为了减少计算量，我们可以乘以dx(这里假设dx是正的，负的就是换一个方向而已，后面会讲到)，乘dx不改变符号

然后就是要找出p的递推式减少计算量，如下

算法的最终步骤如下

至于如果dx或者dy小于0，只是说明他直线前进的方向不一样，这时候只要把上面公式中的+1全部换成-1就行了，然后如果直线的斜率大于1，也就是和直线斜率小于1的那部分直线是关于y=x对称的，所以只要将公式中的x和y换一下就行了。

采用这个算法画三角形，就是用三个点分别两两使用上面的算法求出直线上的所有模拟点，然后像上一次作业那样，按照格式x，y，depth，r，g，b放在一个数组里，接着就调用glDrawArrays(GL_POINTS, 0, point_num); 来将这些点全部画出来就行。（这里就略过那些VAO,VBO那些了，和之前是一样的）。

结果截图：

1. 使用Bresenham算法(只使用integer arithmetic)画一个圆：input为一个2D点(圆心)、一个integer半径；output为一个圆

参考博客https://blog.csdn.net/mmogega/article/details/53055625

首先，是要知道通过中点的圆的对称性，分别关于x轴，y轴，y = x，y = -x对称，所以只要得到八分之一的那部分坐标，其余都能通过这个对称性求得（x, -y）、（-x, y）、（-x, -y）、（y, x）、（y, -x）、（-y, x）、（-y, -x）。而如果是圆心不在原点的就直接通过平移移到原点就行了。

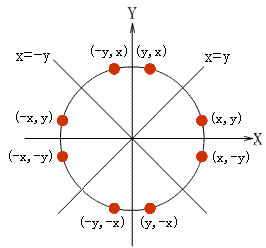
中点画圆法：在八块的第一象限第一块中，如果上一个点确定了，下一个点由于要在格点上，所以只能是（x+1,y）或者是(x+1,y-1)这两个中的一个，类似上面算法的思想，

F(x, y）= x2 + y2 – R2（到圆心的距离）

当F(x, y）= 0，表示点在圆上，当F(x, y）> 0，表示点在圆外，当F(x, y）< 0，表示点在圆内。如果M是P1和P2的中点，则M的坐标是（xi + 1, yi – 0.5），当F（xi + 1, yi – 0.5）< 0时，M点在圆内，说明P1点离实际圆弧更近，应该取P1作为圆的下一个点。同理分析，当F（xi + 1, yi – 0.5）> 0时，P2离实际圆弧更近，应取P2作为下一个点。当F（xi + 1, yi – 0.5）= 0时，P1和P2都可以作为圆的下一个点，算法约定取P2作为下一个点。

然后又是和之前那样对这个中点到圆心距离d的公式推到过程了，目的是求出一个递推式

而且根据这个第一个八分之一块的第一个点是（0，r）可以推出d0

至此好像已经很完美了，但是为了减少使用浮点数运算，我们还要将1.25这个东东变成整数，由于我们只是要看d的符号，一种方法是将d的计算放大两倍，同时将初始值改成3 – 2R，这样避免了浮点运算，乘二运算也可以用移位快速代替，采用3 – 2R为初始值的改进算法，又称为Bresenham算法，有了初值以后就可以像之前那个算法那样一步步迭代了。

具体的实现的话还是就是用上面的算法，求出那八分之一块点的坐标，然后用对称性和平移性求出所有坐标，按格式组成一个vertice数组，接着的画法就是把所有点画出来就行了，和画第一问三角形是一样的。（点的坐标还要进行归一化之类的操作）

截图如下：

1. 在GUI在添加菜单栏，可以选择是三角形边框还是圆，以及能调整圆的大小(圆心固定即可)。

这个就在imgui里调用checkbox来控制一个bool变量，然后分别调用不同的算法来获取点的集合然后用同样的方法画就行了。至于调整圆的大小SliderInt来获取半径再调用算法就行了

截图：

Bonus:

1. 使用三角形光栅转换算法，用和背景不同的颜色，填充你的三角形。

我用的方法是Edge Equation的方法

大概的思路就是如下：先通过三个顶点计算出包含三角形的一个矩形，然后扫描矩形里的每一个点，如果他在计算每个直线方程的结果都大于0，即是在三角形里面的。在求直线方程时，仅通过两个点进行计算不能保证里面的点计算是大于0，所以可以通过第三个点进行验证，因为第三个点肯定是在三角形里的，所以就把第三个点带入已计算出的直线方程中，如果大于0就满足，小于0只要把整个直线方程乘以-1，就是把系数乘以-1就行了。

在实际计算的时候，我感觉这个方法有点慢，因为要计算每一个点，很多点是没用的，所以就直接把点都已经算好了，不在每一帧的时候进行计算，不然太慢了。

实际操作就是用上面的算法把点都求出来，然后在按格式放到数组vertice里，接着的画法就和之前一样了。

截图：

参考博客：https://blog.csdn.net/timso1997/article/details/79732779

最后

以上就是忧虑绿茶为你收集整理的openGL学习过程（2）Bresenham算法画线和圆以及三角形的光栅化的全部内容，希望文章能够帮你解决openGL学习过程（2）Bresenham算法画线和圆以及三角形的光栅化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。