4.7-4.9补题+水题+高维前缀和

题目链接：51nod 1718 Cos的多项式  【数学】

题解：

2cosx=2cosx

2cos2x=(2cosx)^2-2

2cos3x=(2cosx)^3-3*(2cosx)

数归证明2cos(nx)能表示成关于2cosx的多项式,设为f(n)

f(1)=x,f(2)=x^2-2(其中的x就是2cosx)

假设n=1~k时均成立(k>=3)

当n=k+1时

由cos((k+1)x)=cos(kx)cos(x)-sin(kx)sin(x)

cos((k-1)x)=cos(kx)cos(x)+sin(kx)sin(x)

相加得到cos((k+1)x)+cos((k-1)x)=cos(kx)*2cos(x)

从而f(k+1)+f(k-1)=f(k)*x

-> f(k+1)=f(k)*x-f(k-1)

从而成立

这是我们根据递推关系可知对于项的系数和 也满足这个关系式

g(1)=1,g(2)=-1.....于是求这个数列的通项即可。

然后求出循环节：1, -1, -2, -1, 1, 2……

//yy：我第一遍看这题没看懂题目表达的意思。。。傻傻

#include<cstdio>using namespace std;

typedef long long ll;

int a[6] = {1, -1, -2, -1, 1, 2};
int main() {
    ll x;
    scanf("%lld", &x);
    printf("%dn", a[(x-1) % 6]);
    return 0;
}

--------------------------------------------------------------------------------------------------------------------

又做了一遍几道以前做过的水题，卖萌。。。

poj1611 The Suspects 【并查集】

题意：有N个学生，编号为0-N-1，现在0号学生感染了非典，凡是和0在一个社团的人就会感染，并且这些人如果还参加了别的社团，他所在的社团照样全部感染，求感染的人数。

题解：求0号所在的强连通图的结点数。并查集。

我的：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;

const int N = 30005;
int n, m;
int fa[N], rk[N];

void init() {
    for(int i = 0; i < n; ++i) {
        fa[i] = i;
        rk[i] = 1;
    }
}
int fin(int x) {
    if(fa[x] != x) fa[x] = fin(fa[x]);
    return fa[x];
}
void join(int x, int y) {
    if((x = fin(x)) == (y = fin(y))) return;
    fa[x] = y;
    rk[y] += rk[x];//第一遍手残写成rk[y]++
}

int main () {
    int i, j, x, y, cnt, ans;
    while(~scanf("%d%d", &n, &m), n || m) {
        init();
        for(i = 0; i < m; ++i) {
            scanf("%d", &cnt);
            scanf("%d", &x);
            for(j = 1; j < cnt; ++j) {
                scanf("%d", &y);
                join(x, y);
            }
        }
        ans = rk[fin(0)];
        printf("%dn", ans);
    }
    return 0;
}

学弟的代码WA了，然后把判断父节点还是找根那里给他改对了。。。：

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int pre[30005];
int visit[30005];
int find(int xxx)
{
    if(xxx!=pre[xxx])
    return pre[xxx]=find(pre[xxx]);
    else
    return xxx;
}
void join(int ax,int bx)
{
    int axx=find(ax);
    int bxx=find(bx);
    if(axx!=bxx)
    pre[bxx]=axx;
}
int main()
{
    int n,m;
    while(~scanf("%d %d",&n,&m)&&n+m)
    {
        int i,j;
        for(i=0;i<n;i++)
            pre[i]=i;
        memset(visit,0,sizeof(visit));
        visit[0]=1;
        int ans=1;
        for(i=1;i<=m;i++)
        {
            int x;
            scanf("%d",&x);
            int q[30005];
            bool f=false;
            for(j=0;j<x;j++)
            {
                scanf("%d",&q[j]);
                if(find(q[j])==0)
                f=true;
            }
            if(f)
            {
                for(j=0;j<x;j++)
                {
                    join(0,q[j]);
                }
            }
            else
            {
                for(j=1;j<x;j++)
                {
                    join(q[0],q[j]);
                }
            }
        }
        for(i=1;i<n;i++)
        {
            if(find(i)==0)
            ans++;
        }
        printf("%dn",ans);
    }
    return 0;
}

hdu1878 欧拉回路 【并查集判连通 或 dfs判连通】

并查集判连通， 然后判断欧拉回路：无向图 度数为偶

方法一：并查集

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;

const int N = 1005;
int fa[N];
int n, m;
int cnt;
int du[N];

int fin(int x) {
    if(fa[x] != x) fa[x] = fin(fa[x]);
    return fa[x];//第一遍写成返回x,心塞，我好蠢啊。。。
}
void join(int x, int y) {
    if((x = fin(x)) == (y = fin(y))) return ;
    else { fa[x] = y; cnt++; }
}

int main () {
    int x, y, i ,j;
    while(scanf("%d", &n), n) {
        CLR(du, 0);
        for(i = 1; i <= n; ++i) fa[i] = i;
        cnt = 0;

        scanf("%d", &m);
        int f = 0;
        while(m--) {
            scanf("%d%d", &x, &y);
            join(x, y);
            du[x]++;  du[y]++;
        }
        if(cnt == n-1) {
            for(i = 1; i <= n; ++i) {
                if(du[i] % 2 == 1) {
                    f = 1; break;
                }
            }
            if(f) printf("0n");
            else printf("1n");
        }
        else printf("0n");
    }
    return 0;
}

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;

const int N = 1005;
int fa[N];
int n, m;
int cnt;
int du[N];

int fin(int x) {
    if(fa[x] != x) fa[x] = fin(fa[x]);
    return fa[x];
}
void join(int x, int y) {
    if((x = fin(x)) == (y = fin(y))) return ;
    else { fa[x] = y; }
}

int main () {
    int x, y, i ,j;
    while(scanf("%d", &n), n) {
        CLR(du, 0);
        for(i = 1; i <= n; ++i) fa[i] = i;
        cnt = 0;

        scanf("%d", &m);
        int f = 0;
        while(m--) {
            scanf("%d%d", &x, &y);
            join(x, y);
            du[x]++;  du[y]++;
        }
        for(i = 1; i <= n; ++i) {
            if(fa[i] == i) cnt++;
            if(du[i] % 2 == 1) {
                f = 1; break;
            }
        }
        if(f || cnt != 1) printf("0n");
        else printf("1n");
    }
    return 0;
}

方法二：dfs

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;

const int N = 1005;
int n, m;
int du[N];
int g[N][N], vis[N];

void dfs(int x) {
    vis[x] = 1;
    for(int i = 1; i <= n; ++i) {
        if(!vis[i] && g[x][i])
            dfs(i);
    }
}

int main () {
    int x, y, i ,j;
    while(scanf("%d", &n), n) {
        CLR(du, 0);
        CLR(vis, 0);
        CLR(g, 0);

        scanf("%d", &m);
        int f = 0;
        while(m--) {
            scanf("%d%d", &x, &y);
            g[x][y] = g[y][x] = 1;
            du[x]++;  du[y]++;
        }
        dfs(1);
        for(i = 1; i <= n; ++i) {
            if(!vis[i] || du[i] % 2 == 1) {
                f = 1; break;
            }
        }
        if(f) printf("0n");
        else printf("1n");
    }
    return 0;
}

//yy:记得上回去比赛纠结死在格式错误上，水题各种格式错误，回来后改，有一题把string全部改成char就过了，我现在也不知道哪里错了。。。不贴它了，气哭了。。。

题目链接:L1-039. 古风排版 [水题]

//yy：WA的郁闷,姿势太差……

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#include<queue>
#include<limits.h>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long ll;
char s[1005], ans[105][1005];
int main() {
    int i, j, len, row, col, r, c;
    scanf("%d ", &row);
    gets(s);
    len = strlen(s);
    /*WA了。。
    int t = len % row;
    col = len / row + t;
    */
    col = len / row + (len % row == 0 ? 0 : 1);
    for(i = 0; i < row; ++i) {//唉，别漏了啊。。。
        ans[i][0] = ' ';//orz
        ans[i][col] = '';
    }
    r = 0;
    c = col - 1;
    for(i = 0; i < len; ++i) {
        ans[r][c] = s[i];
        r++;
        if(r == row) {
            r = 0;
            c--;
        }
    }
    for(i = 0; i < row ; ++i)
        printf("%sn", ans[i]);
    return 0;
}

-------------------------------------------------------------------------------------------------------------------------

看有大神问高维前缀和，然后抽空随便搜题学习着做一下orz。。。因为对DP害怕，所以还有点迷糊？【晕】

//yy：将集合的 超集状态 合并到 该集合状态上。。。

hdu5765 Bonds 【bfs + 高维前缀和】

官方题解：

参考博客：http://blog.csdn.net/v5zsq/article/details/52170307

题意：给定一个n个点的无向连通图，求每条边被多少个极小割边集包括

题解：极小割边集会把图分成两个连通块，因为至多20个点，所以可用一个20位的二进制数表示一个点集。

先找所有连通点集（可以从一个点的点集开始转移求出所有连通点集，关键是求出任一点集的邻接点，然后从一个连通点集开始，往其中加入这个点集的某个邻接点以及和这个邻接点可达的点就可以构成一个新的连通点集 【通过bfs实现】），然后就得到了所有点集的连通状态，对于某个点集i，如果i是连通的，并且i的补集j是连通的，那么说明i和j之间连的所有边构成一个极小割边集。对这些割边集一一更新答案显然不行，这里就采用对总体累加，对不合法情况累加，然后相减得到答案。

对于u->v：

答案=u和v处于两个不同且互补的连通点集的方法数

= （两个连通点集互补的方法数tot - u和v属于同一个连通点集中的方法数）/2

等式右边第一项可以枚举所有点集i， 如果i和它的补集j都是连通的则tot++，sum[i]++,sum[j]++, sum[i]++说明i这个点集中任意两点处于同一个连通点集的方法数加一，这样做一遍后就得到了tot，但是u,v处于同一个连通点集的方法数还没得到，就考虑到所有包含u和v的点集都是点集{u,v}的超集，因此 可以对sum数组用一遍 高维前缀和，那么右边第二项就为sum[(1<<u) | (1<<v)] 。

//yy：看懂一块知识都会很兴奋。。。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#include<queue>
#include<limits.h>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long ll;
const int N = (1<<20)+5;
const int M = 20*20+5;
int n, m;
int tot;//两个连通点集互补的方法数
int u[M], v[M], reach[N], sum[N];
bool mask[N];//是否是连通点集
int lowbit(int x) {
    return x & (-x);
}
int main() {
    int t, i, j, kase = 1;
    scanf("%d", &t);
    while(t--) {
        CLR(reach, 0);
        CLR(mask, false);
        CLR(sum, 0);
        tot = 0;
        scanf("%d%d", &n, &m);
        for(i = 1; i <= m; ++i) {
            scanf("%d%d", &u[i], &v[i]);
            reach[ 1<<u[i] ] |= 1<<v[i];
            reach[ 1<<v[i] ] |= 1<<u[i];
        }
        //reach[i]表示与i这个点集邻接的点
        for(i = 1; i < (1<<n); ++i)
            reach[i] |= reach[lowbit(i)] | reach[i-lowbit(i)];
        //bfs找所有连通块
        queue<int>q;
        for(i = 0; i < n; ++i) {
            q.push(1<<i);
            mask[1<<i] = true;
        }
        while(!q.empty()) {
            int u = q.front(); q.pop();
            int around = reach[u] ^ u;//u的所有邻接点
            //从一个连通块的邻接点开始扩展找新的连通块
            while(around) {
                int t = lowbit(around) | u;//这个点集的某个邻接点 和 这个邻接点可达的点
                if(!mask[t]) {//新的连通块
                    q.push(t);
                    mask[t] = true;
                }
                around -= lowbit(around);
            }
        }
        for(i = 0; i < (1<<n); ++i) {
            j = ((1<<n)-1) ^ i;//i的补集
            if(mask[i] && mask[j]) {//i和它的补集都连通
                tot++;
                sum[i]++;//i这个点集中任意两点处于同一个连通点集的方法数加一
                sum[j]++;
            }
        }
        //高维前缀和
        for(j = 0; j < n; ++j) {
            for(i = (1<<n)-1; i >= 0; --i) {
                if(!(i & (1<<j)))
                    sum[i] += sum[i | (1<<j)];
            }
        }
        printf("Case #%d:", kase++);
        for(i = 1; i <= m; ++i)
            printf(" %d", (tot - sum[(1<<u[i]) | (1<<v[i])]) / 2);
        puts("");
    }
    return 0;
}

 

hihocoder 1496 : 寻找最大值  【高维前缀 最大和次大】

给定N个数A₁, A₂, A₃, ... A_N，小Ho想从中找到两个数A_i和A_j(i ≠ j)使得乘积A_i × A_j × (A_i AND A_j)最大。其中AND是按位与操作。

时间复杂度O(m*2^m)

//yy：还是别人写的题解，无奈我做不出，只能看了再复写一遍orz，感觉有点套路？：

枚举x&y的结果z，找出两个数x&y==z使得x*y最大，更新答案即可，

条件可以被削弱为z为x&y的子集，这种条件放缩不会导致最优解的丢失，
z为x&y的子集等价于z为x的子集并且z为y的子集。
那么我们只要找出以z为子集的最大值和次大值，然后枚举z即可计算出答案。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<cmath>
#include<queue>
#include<limits.h>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long ll;
const int N = (1<<20)+5;
const int M = 20;
int n;
int tot;
int maxx[N][2];

int main() {
    int t, i, j, x;
    ll ans;
    scanf("%d", &t);
    while(t--) {
        CLR(maxx, 0);
        scanf("%d", &n);
        for(i = 0; i < n; ++i) {
            scanf("%d", &x);
            if(!maxx[x][0]) maxx[x][0] = x;
            else if(!maxx[x][1]) maxx[x][1] = x;
        }
        /*for(i = 0; i < (1<<M); ++i) {
            if(maxx[i][0])
                printf("ma[%d][0]=%dn",i,maxx[i][0]);
            if(maxx[i][1])
                printf("ma[%d][1]=%dn",i,maxx[i][1]);
        }*/
        //puts("");
        //高维前缀 最大 次大
        for(j = 0; j < M; ++j) {
            for(i = (1<<M)-1; i >= 0; --i) {
                if(!(i&(1<<j))) {
                    if(maxx[i][0] < maxx[i | (1<<j)][0]) {
                        maxx[i][1] = maxx[i][0];
                        maxx[i][0] = maxx[i | (1<<j)][0];
                        //printf("ma[%d][0]=%dn",i,maxx[i][0]);
                        //printf("ma[%d][1]=%dn",i,maxx[i][1]);
                    }
                    if(maxx[i][1] < maxx[i | (1<<j)][1]) {
                        maxx[i][1] = maxx[i | (1<<j)][1];
                        //printf("ma[%d][1]=%dn",i,maxx[i][1]);
                    }
                }
            }
        }
        ans = 0;
        for(i = 0; i < (1<<M); ++i)
            ans = max(ans, 1ll*i * maxx[i][0] * maxx[i][1]);
        printf("%lldn", ans);
    }
    return 0;
}

题目链接：codeforces 449 D. Jzzhu and Numbers  【容斥 + 高维前缀和】

题意:给定n个数，求有多少种集合方案数使得ai1&ai2&...&aik = 0

官方题解：

Firstly, we can use inclusion-exclusion principle in this problem. Let f(x) be the count of number i where A_i&x = x. Let g(x) be the number of 1 in the binary respresentation of x. Then the answer equals to .

Now the task is to calculate f(x) for every integer x between 0 and 2²⁰. Let f_k(x) be the count of number i where Y₀&X₀ = X₀ and X₁ = Y₁ (they are defined below).

We divide x and A_i into two parts, the first k binary bits and the other 20 - k binary bits. Let X₀ be the first part of x and X₁ be the second part of x. Let Y₀ be the first part of A_i and Y₁ be the second part of A_i.

We can calculate f_k(x) in O(1):

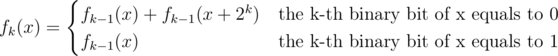
The problem can be solved in O(n * 2ⁿ) now (n = 20 in this problem).

//待补。。。