概述
在每一趟排序中，从待排序子表中选出关键字最小（大）的元素放在其最终位置上。
如何选择最大（小）的关键字？
这一选择方法的不同形成了不同的算法。
本节介绍3种选择排序方法。
目录
1 直接选择排序
视频流程展示
时间复杂度：
Python代码
2 锦标赛排序（也称为树形选择排序 Tree Selection Sort）
视频流程展示
Java代码
时间复杂度：
3 堆排序
堆的定义
堆排序流程
如何由一个无序序列建成一个堆？
时间复杂度为
Python代码：
1 直接选择排序
基本思想：在待排序子表中找出最大（小）元素，并将该元素放在子表的最前（后）面。
https://www.runoob.com/python3/python-selection-sort.html
视频流程展示
直接选择排序
稳定性：不稳定排序
时间复杂度：
比较次数： (n-1)+(n-2)+…+1=n(n-1)/2 —— O()
空间性能：1个辅助空间；
Python代码
A = [64, 25, 12, 22, 11]
for i in range(len(A)):
min_idx = i
for j in range(i + 1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]
print("排序后的数组：")
for i in range(len(A)):
print("%d" % A[i])2 锦标赛排序（也称为树形选择排序 Tree Selection Sort）
代码抄自 ：https://blog.csdn.net/iteye_9368/article/details/82522816
视频流程展示
锦标赛排序shi'pin'yan'shi
也称为树形选择排序（Tree Selection Sort），是一种按照锦标赛的思想进行选择排序的方法。
首先对n个记录进行两两比较，然后优胜者之间再进行两两比较，如此重复，直至选出最小关键字的记录为止。
这个过程可以用一棵有n个叶子结点的完全二叉树表示。
根节点中的关键字即为叶子结点中的最小关键字。
在输出最小关键字之后，欲选出次小关键字，
仅需将叶子结点中的最小关键字改为“最大值”，如∞，
然后从该叶子结点开始，和其兄弟的关键字进行比较，
修改从叶子结点到根的路径上各结点的关键字，
最后根结点的关键字即为次小关键字。
Java代码
public class TreeSelectSort {
public static int[] TreeSelectionSort(int[] mData) {
int TreeLong = mData.length * 4;
int MinValue = -10000;
int[] tree = new int[TreeLong]; // 树的大小
int baseSize;
int i;
int n = mData.length;
int max;
int maxIndex;
int treeSize;
baseSize = 1;
while (baseSize < n) {
baseSize *= 2;
}
treeSize = baseSize * 2 - 1;
for (i = 0; i < n; i++) {
tree[treeSize - i] = mData[i];
}
for (; i < baseSize; i++) {
tree[treeSize - i] = MinValue;
}
// 构造一棵树
for (i = treeSize; i > 1; i -= 2) {
tree[i / 2] = (tree[i] > tree[i - 1] ? tree[i] : tree[i - 1]);
}
n -= 1;
while (n != -1) {
max = tree[1];
mData[n--] = max;
maxIndex = treeSize;
while (tree[maxIndex] != max) {
maxIndex--;
}
tree[maxIndex] = MinValue;
while (maxIndex > 1) {
if (maxIndex % 2 == 0) {
tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex + 1] ? tree[maxIndex]
: tree[maxIndex + 1]);
} else {
tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex - 1] ? tree[maxIndex]
: tree[maxIndex - 1]);
}
maxIndex /= 2;
}
}
return mData;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int array[] = { 38, 62, 35, 77, 55, 14, 35, 98 };
TreeSelectionSort(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println("n");
}
}时间复杂度：
O(nlog2n)
辅助空间为n-1, 空间复杂度为O(n-1).
缺点：辅助存储空间较多、最大值进行多余的比较
3 堆排序
https://www.runoob.com/python3/python-heap-sort.html
堆排序：利用堆进行的排序。
定义：称n个元素组成的序列(a1,a2,…，an) 为堆， 当且仅当满足下面关系。（其中ki是元素ai的关键字）
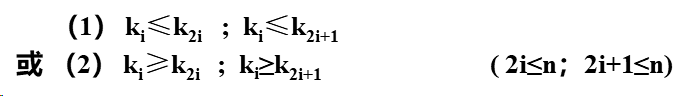
如果将此序列对应到编号的完全二叉树：
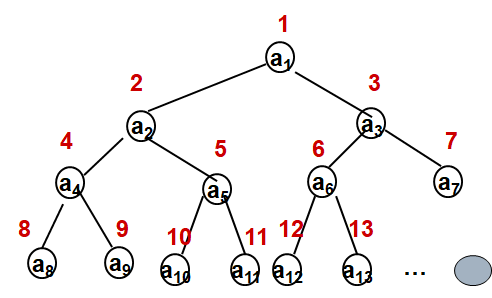
堆的定义
可用完全二叉树中的有关术语解释为：每一结点均不大于(或不小于）其左、右孩子结点的值。
若序列(a1,a2,…,an)是堆，则堆顶(完全二叉树的根)必为序列中的最小或最大值。
将根最大的堆称为大根堆，根最小的堆称为小根堆.
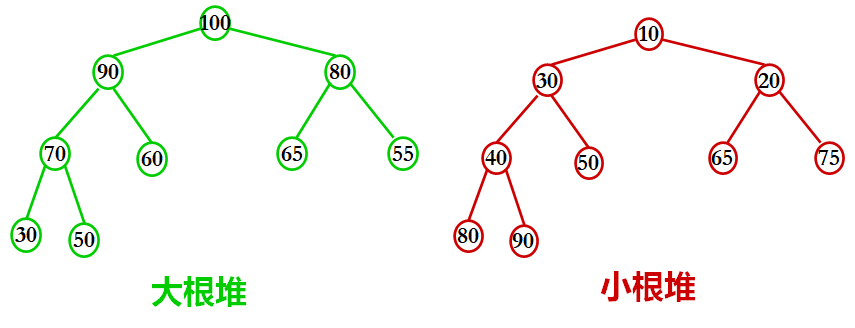
例： 判断下面数据是否是堆：(5,23,16,68,64,72,71,73,45,79,90,81,75,94,97)
解：对应的二叉树形式如下：（45<68!!!)序号9那地儿不行
实现堆排序还需要解决两个问题：
（1）如何由一个无序序列建成一个堆？
（2）如何在输出堆顶元素之后，调整剩余元素成为一个新的堆？
问题（2）的解决方法是：
在输出堆顶元素之后，以堆中最后一个元素替代之，此时根结点的左、右子树均为堆，则仅需自上至下进行调整即可。
我们称自堆顶至叶子的调整过程为“筛选”。
问题1的解决方法是：
从一个无序序列建堆的过程就是一个反复“筛选”的过程。若将此序列看成是一个完全二叉树，则最后一个非终端结点是第⌞n/2⌟个元素，由此“筛选”只需从第⌞n/2⌟个元素开始。
堆排序流程
堆排序
（约定进行增排序，因而采用大根堆）
如果初始序列是堆，则可通过反复执行如下操作而最终得到一个有序序列：
筛选过程即输出根：即将根（第一个元素）与当前子序列中的最后一个元素交换。
调整堆：将输出根之后的子序列调整为堆。
如果初始序列不是堆，则首先要将其先建成堆，然后再按（1）的方式来实现。
如何由一个无序序列建成一个堆？
建立堆操作
- 通过反复调用筛选操作来实现。
- 建堆过程要从下往上逐棵子树地进行筛选，即根的下标按照从n/2到1的次序将各子树调整为堆。
时间复杂度为
。
Python代码：
def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # 交换
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
n = len(arr)
print("排序后")
for i in range(n):
print("%d" % arr[i])
最后
以上就是活泼热狗为你收集整理的选择排序（直接选择排序 & 锦标赛排序 & 堆排序）1 直接选择排序2 锦标赛排序（也称为树形选择排序 Tree Selection Sort）3 堆排序的全部内容，希望文章能够帮你解决选择排序（直接选择排序 & 锦标赛排序 & 堆排序）1 直接选择排序2 锦标赛排序（也称为树形选择排序 Tree Selection Sort）3 堆排序所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复