python 遗传算法_遗传算法(Python) #2 基本运算方法详解

上一期

1.遗传算法主要流程

用遗传算法来解决最优化问题的解的基本如下流程如下：

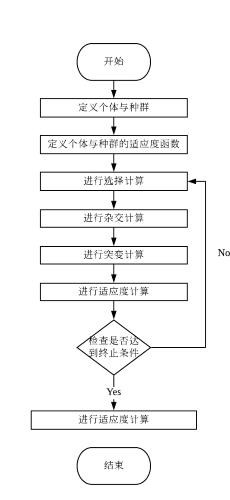
流程简介：

1. 定义种群与个体：遗传算法中每个个体即为问题的解，一般个体按照一定方法随机生成。
2. 定义个体与种群的适应度函数：个体的适应度函数可以用于选择个体，而种群的适应度函数可以用来追踪算法的进度。
3. 循环选择、杂交、突变与适应度计算：这一系列操作可以生成下一代的个体选择：一般而言以更大的概率选择适应度更高的个体杂交：交换不同个体之间的基因突变：随机在个体的基因中产生突变计算该世代的适应度：每个世代的总/平均适应度或适应度的方差等可以用来追踪算法的进度。
4. 检测终止条件：若满足终止条件，则停止迭代
5. 获得最优解：一般选择适应度最高的个体作为解

之后本文将对每一步的具体做法做出详细说明。

2. 定义种群与个体

1. 定义个体

因为每个个体都由一系列基因组成，所以一般而言可以将个体定义为一个列表(List)。当然，也可以将个体定义为一个字典(Dictionary)或类(Class)，从而运用更多python中的方法。具体问题需要具体分析。若使用专门的遗传算法框架(如DEAP, Pybrain等)，则可使用框架内提供方法，一般而言利用框架可以极大的减少代码量。

2. 定义种群

一系列个体可以构成种群，所以一般可以将种群定义为由所有个体组成的列表。 当然，你可以进一步将该列表封装成一个类，或使用遗传算法的框架来定义。

3. 定义种群与个体的适应度函数

1. 个体的适应度函数

通过适应度函数，我们可以计算每个个体的适应值，并用于个体的选择(Select).一般而言取最大值，但如果某个问题时需要求最小值，我们给适应度函数乘以-1。

2. 种群的适应度函数

种群的适应度函数可以用来追踪遗传算法的进度，比如当种群的适应度函数在100次迭代中都没有明显的变化，我们可以认为该种群已经不再进化，可以停止迭代过程。一般而言，我们可以定义种群的适应度函数为所有个体的最大值、平均值、方差等。

4. 循环进行选择，杂交、突变与适应度计算

1. 选择(Selection)

每次迭代中，我们一般以更高的概率选择适应度更高的个体.假如我们的种群中有以下五个个体：

• 个体A：适应度 20，占比 38.5%
• 个体B: 适应度 15，占比 28.8%
• 个体C：适应度 10，占比 19.2%
• 个体D：适应度 5，占比 9.6%
• 个体E：适应度 2，占比 3.8%

主要的选择方法如下：

1.锦标赛法 (Rank-Based Selection)

如字面意思一样，锦标赛法就是从种群的n个个体中随机抽取k个个体，并按照锦标赛的方法选择出适应度更高的个体：

• 方法一：从种群的n个个体中随机抽取k个个体，直接选择适应度最高的个体。无需真正让个体两两之间进行一轮一轮的锦标赛，因为适应度最高的个体必将胜出。
• 方法二：从种群的n个个体中随机抽取k个个体，进行两两锦标赛，并按概率选择排名靠前的j个个体。(j < k < n)

以ABCDE组成的种群为例，假设在一次锦标赛中我们随机抽取了BDE三个个体：

• 方法一：因为B的适应度最高，所以我们直接选择B
• 方法二：假设我们以更高的概率选取锦标赛中的前两名第一轮：B与D进行锦标赛，B胜出第二轮：E轮空，直接进入决赛第三轮：B与E进行锦标赛，B第一名，E第二名(虽然E的适应度比D还要小)最后，我们可以0.9的概率选择B，并以0.1的概率选择E。

通过比较方法一与方法二可见，按照方法二进行锦标赛可以增加一些随机性，从而降低算法提前收敛的概率。

2.轮盘法(Roulette Wheel selection)

轮盘法就是按照适应度比例随机选取个体，示意图如下：

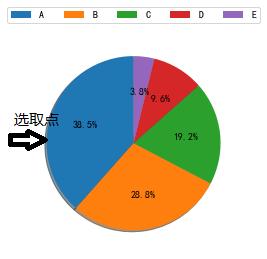
假设选择点如图所示，我们可以转动转盘，并选择选择点所指向的个体，为了保持种群大小不变，我们可以转动转盘五次并随机选择五个对应的个体。

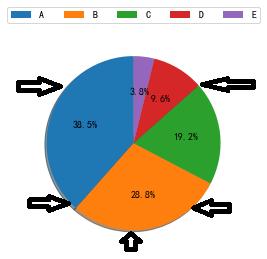
3.随机普遍取样法(Stochastic Universal Sampling)

如图所示，虽然仍然使用同样的轮盘，但我们只旋转轮盘一次，取等距的五个选择点，并选择对应的个体，与普通的轮盘法相比，随机普遍采样可以增加适应度较低的个体被选中的概率，从而增加种群的多样性。

4.排名法(Rank-Based Selection)

排名法仍然用轮盘法或随机普遍取样法来选取个体，但区别是排名法用个体的适应度排名排名来计算被选择的概率，而不是适应度本身，示意图如下：

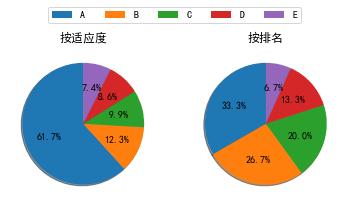
假设有五个个体VWXYZ(如上图)，其适应度，适应度占比，排名，排名(由小到大)占比为

1. 个体 V: 适应度 50，占比 61.7%;排名5，排名占比 33.3%
2. 个体 W: 适应度 10，占比 12.3%;排名4，排名占比 26.7%
3. 个体 X: 适应度 8，占比 9.9%;排名3，排名占比 20.0%
4. 个体 Y: 适应度 7，占比 8.6%;排名2，排名占比 13.3%
5. 个体 Z: 适应度 6，占比 7.4%;排名1，排名占比 6.7%

由上图比较可以看出，当不同个体之间的适应度差异较大时，使用排名法可以让适应度小的个体更容易被选中，某些情况下使用排名法更恰当。

5.适应度的线性变换

与排名法类似，有时直接用适应度选择会导致适应度高的个体太容易被选中，而适应度低的个体不容易被选中，若遇到这样的情况，我们可对适应度进行线性变化，从而让适应度低的个体更容易被选中，选择时，我们同样可以采取轮盘法或随机普遍采样法：

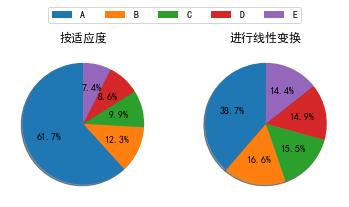
假设有五个个体VWXYZ(如上图)，为了让适应度低的个体更容易被选中，我们对适应度进行以下线性变换： 新适应度 = 0.5 * 原适应度 + 10

其适应度，适应度占比，变换后适应度，变换后适应度占比分别为

1. 个体 V: 适应度50，占比61.7%;适应度35，适应度占比 38.7%
2. 个体 W: 适应度10，占比12.3%;适应度15，适应度占比 16.6%
3. 个体 X: 适应度8，占比9.9%;适应度14，适应度占比 15.5%
4. 个体 Y: 适应度7，占比8.6%;适应度13.5，适应度占比 14.9%
5. 个体 Z: 适应度6，占比7.4%;适应度13，适应度占比 14.4%

可见，通过线性变换，我们可以改变个体被选择的概率，上述例子里我们提高了适应度低的个体被选中的概率，按照需求不同，我们也可以降低适应度低的个体被选择的概率。

6.精英策略(Elitism)

精英策略就是每次迭代中，在种群的n个个体中，选择适应度最高的k个个体(k 远小于 n)，不进行杂交或突变而进入下一次迭代。

虽然一般而言，种群的整体适应度都会向着更高的方向发展，但杂交和突变降低个体的适应度，举一个直观的例子，假设适应度对应人的美观程度，爸妈是帅哥美女，但生出来一个丑孩子的情况虽然少，但也可能发生。为了防止这样的情况发生，我们可以保留(或克隆)适应度高的个体，不进行杂交和突变，直接进入下一次的迭代。

2. 杂交(Crossover)

遗传算法中的杂交类似于自然界中的杂交： 亲代相互交换遗传物质(基因组/染色体片段)并产生后代。在遗传算法中，为了保持种群数量不变，亲代杂交一般产生两个后代。

1.单点杂交(Single-Point Crossover)

单点杂交即在基因组中随机选取一点，亲代在该点之后的基因进行交换。

若个体的基因组由二进制字符串来表示，如下所示，上下两个亲代(左)进行杂交并产生两个后代(右),其中“|”代表杂交点：

• 亲代1：1001|1111 -> 后代1：1001|0000
• 亲代2：1000|0000 -> 后代2：1000|1111

2.两点杂交(Two-Point Crossover)

两点杂交即在基因组中随机选取两点，亲代两点之间的基因进行交换。

若个体的基因组由二进制字符串来表示，如下所示，上下两个亲代(左)进行杂交并产生两个后代(右),其中“|”代表杂交点：

• 亲代1：1001|11|11 -> 后代1：1001|00|11
• 亲代2：1000|00|00 -> 后代2：1000|11|00

3.多点杂交(k-Point Crossover)

多点杂交即在基因组中随机选取k个点，亲代在k个点所组成的片段之间交换基因。

若个体的基因组由二进制字符串来表示，如下所示，上下两个亲代(左)进行杂交并产生两个后代(右),其中“|”代表杂交点,亲代交换第1、2和3、4个杂交点之间的基因：

• 亲代1：100|11|1|1|1 -> 后代1：100|00|1|0|1
• 亲代2：100|00|0|0|0 -> 后代2：100|11|0|1|0

4.均匀杂交(Uniform Crossover)

均匀杂交即基因组的每个基因都以p的概率进行杂交(0

若基因组中每个基因用数字0~9来表示，并且p取50%，则每个基因都有50%的概率进行杂交，示意图如下(假设第1，3，5个基因进行了杂交)：

• 亲代1：123456 -> 后代1：624426
• 亲代2：654321 -> 后代2：153351

5.有序杂交(Ordered Crossover)

根据定义不同，假如基因用有序序列来表示，为了尽量不改变亲代中原有顺序，可用以下方式来进行杂交,其中“|”代表突变点，“*”代表待确定的基因：

1. 随机选取两个突变点，并交换突变点之间的基因，突变点外的基因待定：

• 亲代1：1|23|45 -> 后代1：*|31|**
• 亲代2：2|31|54 -> 后代2：*|23|**

2. 以亲代1为后代1的蓝图，逐一确定*位置的基因：

• 从亲代1的突变点后一位开始，4不存在于后代1中，将4填入后代1突变点后第一个位置，后代1变为：*|31|4*
• 亲代1中4的下一位是5，5不存在于后代1中，将5填入后代1，后代1变为：*|31|45
• 亲代1中5的下一位是1，1已存在于后代1中，跳过
• 亲代1中1的下一位是2，2不存在于后代1中，将1填入后代1，后代1变为：2|31|45

3. 以亲代2为后代2的蓝图，逐一确定*位置的基因：

• 从亲代2的突变点后一位开始，5不存在于后代2中，将5填入后代2突变点后第一个位置，后代2变为：*|23|5*
• 亲代2中5的下一位是4，4不存在于后代2中，将4填入后代2，后代2变为：*|23|54
• 亲代2中4的下一位是2，2已存在于后代2中，跳过
• 亲代2中2的下一位是3，3已存在于后代2中，跳过
• 亲代2中3的下一位是1，1不存在于后代2中，将1填入后代2，后代2变为：1|23|54

通过以上方法，可以在杂交的同时保持亲代基因的顺序，这种杂交方法可以用于某些特定的问题，比如旅行推销员问题(Travelling Salesman Problem)。

6. 混合杂交(Blend Crossover)

假设个体的基因组用实数表示，直接交换对应基因上的数字意义不大，这个时候我们可以用混合杂交法，即后代的基因随机取值于由亲代基因构成的范围之内，而这个范围是：

[p1 - a(p2-p1),p2+a(p2-p1)]

• 其中p1,p2分别代表亲代中对应基因的数值(p1 < p2)
• a是一个常数(遗传算法中一般取a=0.5)

不难发现，该公式有以下性质：

1. a=0时，后代基因的取值范围是[p1,p2]，即后代基因的取值范围不可能超过亲代。
2. a=0.5时，后代基因的取值范围是[1.5p1 - 0.5p2,-0.5p1 + 1.5p2]，该范围的大小是2(p2-p1),为a=0时的两倍
3. a=1时，后代基因的取值范围是[2p1 - p2,-p1 + 2p2],该范围大小是3(p2-p1),为a=0时的三倍

假设我们有以下两个个体，并且a=0.5：

• 亲代1： [10.0, 5.0 , 8.0]
• 亲代2： [2.0 , 12.0, 6.0]

套用公式：[p1 - a(p2-p1),p2+a(p2-p1)]，则杂交产生的后代每个基因的取值范围分别是：

• 基因1：[-2.0, 14.0]
• 基因2：[1.5 , 15.5]
• 基因3：[5.0 , 9.0]

7. 模拟二进制杂交(Simulated Binary Crossover)

当个体基因由实数表示时，模拟二进制杂交借用了单点杂交(Single-Point Crossover)的概念，其目的是模拟单点杂交中后代基因的均值与亲代相同的这一性质，后代的基因数值可由以下公式求得：

• o1 = 0.5( (1+a)p1 + (1-a)p2)
• o2 = 0.5( (1-a)p1 + (1+a)p2)

其中：

• o1,o2表示后代1与后代2基因的数值
• p1,p2表示亲代1与亲代2基因的数值
• a为常数，且 a >= 0

不难发现该公式有以下性质：

1. 后代基因的均值永远和亲代相同
2. a=0时，o1 = o2 = 0.5(p1 + p2),后代基因为亲代基因的均值
3. 0 < a < 1时，相对亲代而言，后代之间基因的值更加接近
4. a = 1时，o1 = p1, o2 = p2， 后代与亲代相同
5. a > 1时，相对亲代而言，后代之间的基因值差异更大

3. 突变(Mutation)

与生物学中突变的概念类似，遗传算法中的突变即个体的基因发生随机的改变，而突变主要有以下方法， 不同的突变方法适用于不同的具体问题。

1. 位翻转突变法(Flip Bit Mutation)

位反转突变即染色体上的一个或多个位置发生随机的改变，如：

10001 -> 11001， 第二个位置的0突变为1。

2. 交换突变法(Swap Mutation)

交换突变即染色体上随机的两个基因位置交换，如：

12345 -> 52341， 第一个和最后一个基因交换。

3. 反转突变法(Inversion Mutation)

反转突变即染色体上的一段基因顺序逆转，如：

123456 -> 126543， 第二至第六个位置发生反转突变。

4. 随机打乱突变法(Scramble Mutation)

随机打乱突变即染色体上的一段基因顺序被打乱后重组，如：

123456 -> 126345， 第二至第六个位置的基因被打乱后重组。

5. 实数突变法(Real Mutation)

当个体的基因用实数表达时，可使用实数突变法来产生变异。

其具体方法是，我们首先人为规定一个能产生随机数的函数(一般取正态分布函数，且一般均值取0以保证突变方向的随机性，而标准差可以依问题而定)。突变后基因的值 = 突变前基因的值 + 随机数。

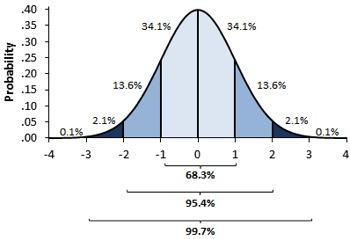
4. 重新计算个体与种群的适应度(Evaluation)

每当一次迭代结束时(已经完成选择，杂交和突变)，我们都应该计算并储存个体与种群的适应度，这些数据有利于我们追踪基因算法的进度，并判断算法是否应该中止。若实时追踪每次迭代后的种群的适应度，我们还可以判断我们的算法是否出现了问题，及时停止迭代并对算法做出修正。

5. 定义算法的终止条件(Stopping Condition)

一个算法一般而言不会无限的运行下去，我们需要定义一些条件来判断算法是否需要被终止，常见的终止条件如下：

1. 按照时间来决定是否终止：从程序开始运行时已经过一定时间，或已经迭代一定次数。
2. 按照成本来决定是否终止：迭代到一定次数时是否已消耗一定的CPU，内存或硬盘储存空间。
3. 按种群性质来决定是否终止：种群是否已经丧失多样性，停止进化，种群适应度是否已经无显著提高。

6. 获得最优解

一般而言，当迭代结束时，适应度最高的个体即为最优解。然而，在迭代中最优的个体可能因为杂交或突变而在某一时刻丢失，为了防止这样的情况发生，我们可以创建一个列表来储存每次迭代中的最优个体，并在迭代结束后从中选择适应度最高的个体作为解。

7. 小结

本文章介绍了遗传算法中如何定义个体与种群，如何进行选择、杂交、突变与适应度的计算，本系列的下一篇文章中我们将不依靠任何已有的框架，用Python来实现遗传算法在OneMax问题中的应用。