Count Complete Tree Nodes 完全二叉树的节点个数

输入: 
    1
   / 
  2   3
 /   /
4  5 6

输出: 6

思路：

最简单的思路就是采用后续遍历，暴力法，逐个数，但是这样的效率很低，而且题目改了test case，这样的代码容易TlE（Time Limit Exceeded），所以我们要充分利用题目给定的条件来解题，提高时间效率。

观察到题目给的的完全二叉树，即除了最后一层外，其余层都是每个节点有两个子节点，这样的树结构如果不考虑最后一层，假设有h层（不包含最后一层），则节点总数可以通过等比数列求出：2^h-1。所以我们对每层节点都判断左子树的深度和右子树的深度是否相同，如果相同那整棵树都是满二叉树，可以直接求总结点数。如果不相同则1（自己的节点数）+左子树递归调用节点总数+右子树递归调用节点总数。

代码如下：

    int countNodes(TreeNode* root) {
	if (!root) {
		return 0;
	}
	TreeNode* l = root, *r = root;
	int left = 0;
	int right = 0;
	while (l) {
		l = l->left;
		left++;
	}
	while (r) {
		right++;
		r = r->right;
	}
	if (left == right) {
		int res = 1;
		for (int i = 0; i < left; i++) {
			res =res<< 1;
		}
		return res - 1;
	}
	return 1 + countNodes(root->left) + countNodes(root->right);        
    }

方法2：

我们可以在上述基础上改进算法减少时间，观察到移位操作不用一位一位移，可以直接

res=res<<left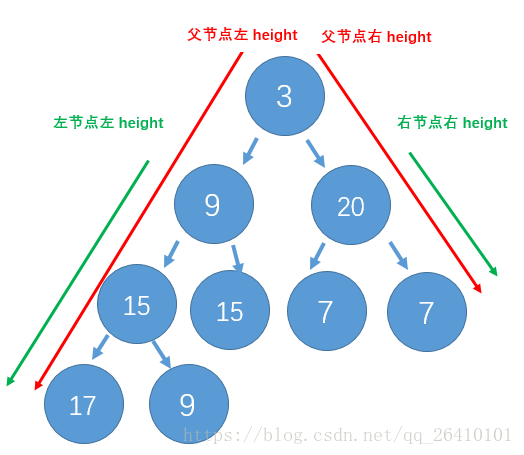

代码如下：

int countNodesCore(TreeNode* root,int left_depth,int right_depth) {
	if (!root) {
		return 0;
	}
	if (left_depth < 0) {
        left_depth=0;
		TreeNode* tmp = root;
		while (tmp) {
			left_depth++;
			tmp = tmp->left;
		}
	}
	if (right_depth < 0) {
        right_depth=0;
		TreeNode* tmp = root;
		while (tmp) {
			right_depth++;
			tmp = tmp->right;
		}
	}
	if (left_depth == right_depth) {
		return (1 << left_depth) - 1;
	}
	return 1 + countNodesCore(root->left, left_depth - 1, - 1) + countNodesCore(root->right, - 1, right_depth - 1);
}
int countNodes(TreeNode* root) {
	if (!root) {
		return 0;
	}
	return countNodesCore(root, -1, -1);
}

其中传入left_depth和right_depth如果小于0表示已经左height或右height已经失效了，需要重新计算。

时间的提升还是很明显的！

输入: 
    1
   / 
  2   3
 /   /
4  5 6

输出: 6

最后

以上就是俏皮大白为你收集整理的Count Complete Tree Nodes 完全二叉树的节点个数的全部内容，希望文章能够帮你解决Count Complete Tree Nodes 完全二叉树的节点个数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。