2018.5.26（求完全二叉树的结点个数）

完全二叉树：
一棵树去除掉最大阶层后为一满二叉树，且阶层最大那层的结点均向左靠齐，则该二叉树为完全二叉树；

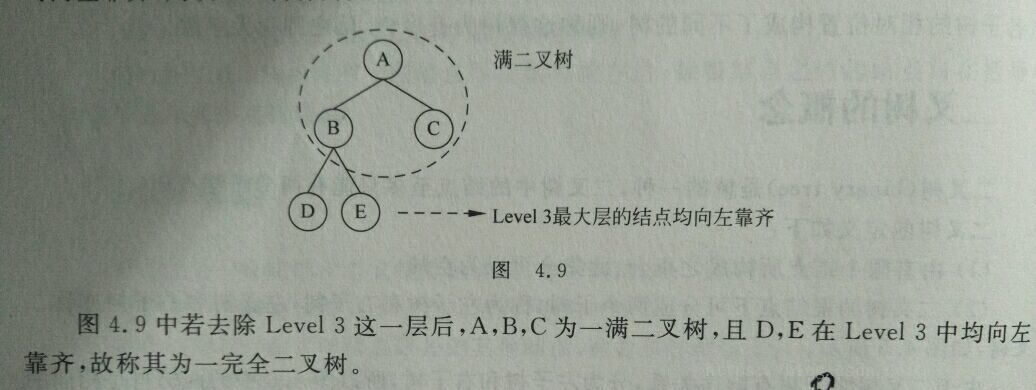
求完全二叉树的结点个数要求时间复杂度低于O(n)

思路剖析：
调用递归解决问题，先求出当前树的深度，在判断当前根结点的左右子树哪个为满二叉树，如果左二叉树为满二叉树，调用递归函数Is_FBT(head->right,total_node+pow(2,depth));反之，调用Is_FBT(head->left,total_node+pow(2,depth-1));

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;

class Tree
{
public:
    int data;
    Tree *left,*right;
    Tree(int value);
};

Tree::Tree(int value)
{
    data=value;
    left=NULL;
    right=NULL;
}

int Depth(Tree *head)
{
    Tree *new_point=head;

    int depth=0;
    while(new_point!=NULL)
    {
        depth++;

        new_point=new_point->left;
    }

    return depth;
}

int Is_FBT(Tree *head,int total_node)
{
    if(head->right==NULL&&head->left==NULL)
        return total_node+1;
    if(head->right==NULL)
        return total_node+2;
    if(head->left==NULL)
        return total_node+1;

    int depth=Depth(head)-1;
    int d=depth;
    Tree *new_point=head->right;

    while(--d&&new_point!=NULL)
        new_point=new_point->left;

    if(d==0)//如果d==0说明左子树为满二叉树，下一次递归当前根节点的右孩子；
        Is_FBT(head->right,total_node+(1<<depth));
    else//如果b!=0，说明右子树为满二叉树，且层数为depth-1,下一次递归当前根节点的左孩子；
        Is_FBT(head->left,total_node+(1<<(depth-1)));
}
int main()
{
    Tree *root=new Tree(1);
    root->left=new Tree(2);
    root->right=new Tree(3);

    int sum=Is_FBT(root,0);

    printf("The total_node of this tree is:n");
    cout<<sum<<endl;

    delete root;
    return 0;
}

//坑~~~~~
    /*while(--d&&new_point!=NULL)//如果改成d--，当前树下，跳出循环后d=-1;
        new_point=new_point->left;*/

    /*int a1=3;
    while(--a1);
    printf("a=%dn",a1);
    int a2=3;
    while(a2--);
    printf("a2=%dn",a2);*/
    //输出结果a1=0,a2=-1;
    //注意区分while(a--)和while(--a)的差别；

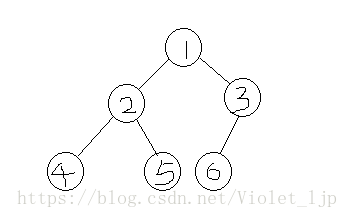
如果当前树为此种状态：
当前树深度为depth=3，定义变量right_depth为右子树深度，当right_depth=depth时，说明左子树为满二叉树，右图可知以2为父结点，4，5为子树的数为满二叉树，根据满二叉树的结点计算公式，此满二叉树共有2^2-1个结点，再加上根节点，共有2^2个结点，调用递归函数Is_FBT(head->right,total_node+pow(2,depth));接着递归调用，执行下一状态；
直到满足递归结束条件

最后

以上就是背后皮皮虾为你收集整理的2018.5.26（求完全二叉树的结点个数）的全部内容，希望文章能够帮你解决2018.5.26（求完全二叉树的结点个数）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。