二叉树的递归套路
- 二叉树
- 如何设计一个打印整棵树的打印函数
- 返回节点的后继节点
- 打印纸条对应折痕方向
- 二又树的递归套路
- 总结
- 判断平衡二叉树
- 判断满二叉树
- 判断完全二叉树
- 非递归思想:
- 递归思想:
- 用大量数据测试
- 二叉树最大距离
- 最大的二叉搜索子树的头节点
- 最大的二叉搜索子树的头节点
- 最小公共祖先
- 无递归思想:
- 递归套路版:
- 大量数据测试
- 派对的最大快乐值
二叉树
如何设计一个打印整棵树的打印函数
package BinaryTree;
public class PrintBinaryTree {
public static class Node{
public int value;
public Node left;
public Node right;
public Node(int data){
this.value=data;
}
}
public static void printTree(Node head){
System.out.println("BinaryTree");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height,String to, int len){
if (head==null) {
return;
}
printInOrder(head.right, height+1, "v", len);
String val=to+head.value+to;
int lenM=val.length();
int lenL=(len-lenM)/2;
int lenR=len-lenM-lenL;
val=getspace(lenL)+val+getspace(lenR);
System.out.println(getspace(height*len)+val);
printInOrder(head.left, height+1, "^", len);
}
public static String getspace(int num){
String space=" ";
StringBuffer buf=new StringBuffer(" ");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(-222222222);
head.right = new Node(3);
head.left.left = new Node(Integer.MIN_VALUE);
head.right.left = new Node(55555555);
head.right.right = new Node(66);
head.left.left.right = new Node(777);
printTree(head);
head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.right.left = new Node(5);
head.right.right = new Node(6);
head.left.left.right = new Node(7);
printTree(head);
head = new Node(1);
head.left = new Node(1);
head.right = new Node(1);
head.left.left = new Node(1);
head.right.left = new Node(1);
head.right.right = new Node(1);
head.left.left.right = new Node(1);
printTree(head);
}
}
返回节点的后继节点
二叉树结构定义如下
class Node{
V Value;
Node left;
Node right;
Node Parent;
}
给你二叉树的某节点,让你返回该点的后继节点
思路:如果某个节点的最右上面是x,那么这个结点就是x的后继
package BinaryTree;
public class SuccessorNode {
public static class Node{
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data){
this.value=data;
}
}
public static Node getSuccessorNode(Node node){
if (node==null) {
return node;
}
if (node.right!=null) {
return getLeftMost(node.right);
}
else {//无右树
Node parent=node.parent;
while (parent!=null && parent.right==node) {//当前结点是父亲结点的右孩子
node=parent;
parent=node.parent;
}
return parent;
}
}
public static Node getLeftMost(Node node){
if (node==null) {
return node;
}
if (node.left!=null) {
node=node.left;
}
return node;
}
public static void main(String[] args) {
Node head=new Node(6);
head.parent = null;
head.left = new Node(3);
head.left.parent = head;
head.left.left = new Node(1);
head.left.left.parent = head.left;
head.left.left.right = new Node(2);
head.left.left.right.parent = head.left.left;
head.left.right = new Node(4);
head.left.right.parent = head.left;
head.left.right.right = new Node(5);
head.left.right.right.parent = head.left.right;
head.right = new Node(9);
head.right.parent = head;
head.right.left = new Node(8);
head.right.left.parent = head.right;
head.right.left.left = new Node(7);
head.right.left.left.parent = head.right.left;
head.right.right = new Node(10);
head.right.right.parent = head.right;
Node test = head.left.left;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.left.left.right;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.left;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.left.right;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.left.right.right;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.right.left.left;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.right.left;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.right;
System.out.println(test.value + " next: " + getSuccessorNode(test).value);
test = head.right.right; // 10's next is null
System.out.println(test.value + " next: " + getSuccessorNode(test));
}
}/*1 next: 2
2 next: 3
3 next: 4
4 next: 5
5 next: 6
6 next: 8
7 next: 8
8 next: 9
9 next: 10
10 next: null
打印纸条对应折痕方向
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N,代表纸条都从下边向上方连续对折N次。请从上到下打印所有折痕的方向。
例如:N=1时,打印:down N=2时,打印:down down up
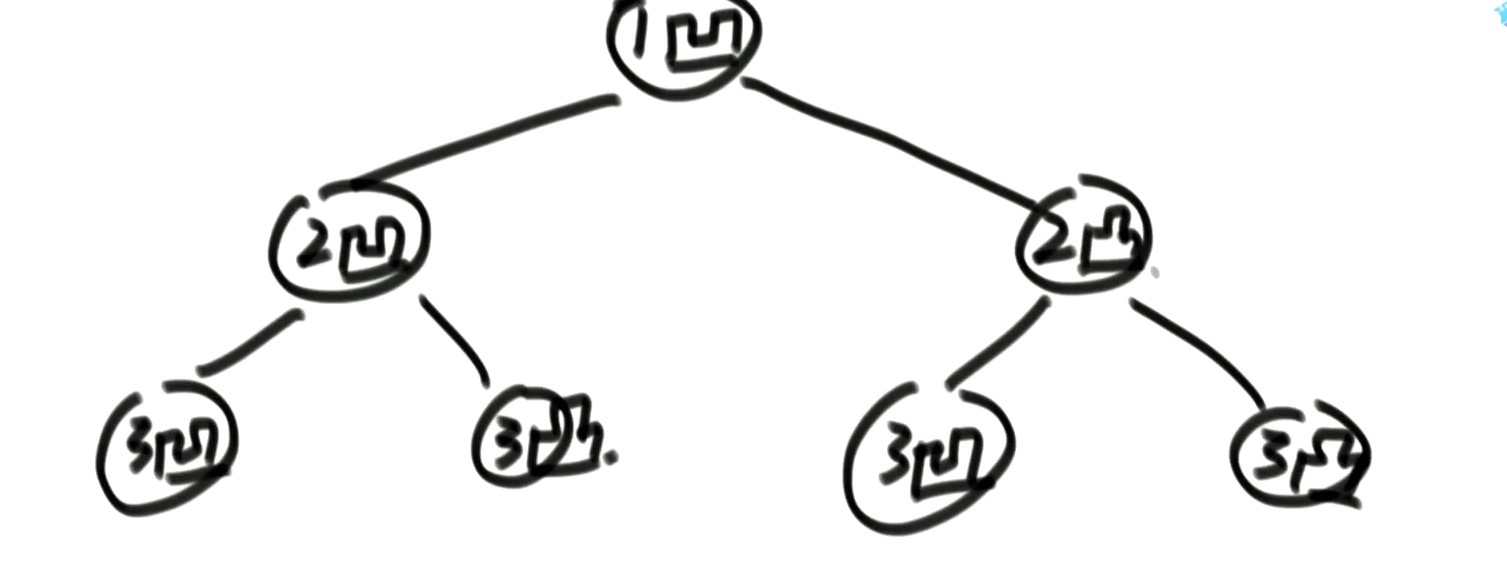 思路:
思路:
当前你来了一个节点,脑海中想象的!
这个节点在第i层,一共有N层,N固定不变的
这个节点如果是凹的话,down = T
这个节点如果是凸的话,down = F
函数的功能:中序打印以你想象的节点为头的整棵树!
package BinaryTree;
public class PaperFolding {
public static void printAllFold(int N){
Printprocess(1,N,true);
}
public static void Printprocess(int i,int N,boolean down){
if (i>N) {
return;
}
Printprocess(i+1, N,true);
System.out.println(down ?"凹":"凸");
Printprocess(i+1, N,false);
}
public static void main(String[] args) {
int N=3;
printAllFold(N);
}
}
/*凹
凹
凸
凹
凹
凸
凸
二又树的递归套路
总结
1)假设以X节点为头,假设可以向X左树和X右树要任何信息
2)在上一步的假设下,讨论以X为头节点的树,得到答案的可能性(最重要)
3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息
4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S
5)递归函数都返回S,每一棵子树都这么要求
6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
判断平衡二叉树
给定一个二叉树的头结点,返回这个二叉树是不是平衡二叉树
特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
package BinaryTree;
public class IsBalanced {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static boolean process1(Node head){
return process(head).IsBalanced;
}
public static class Info{
public boolean IsBalanced;
public int height;
public Info(boolean b,int h){
IsBalanced=b;
height=h;
}
}
public static Info process(Node X){
if (X==null) {
return new Info(true, 0);
}
Info leftInfo=process(X.left);
Info rightInfo=process(X.right);
int height=Math.max(leftInfo.height, rightInfo.height)+1;//加的是头节点的高度
boolean IsBalanced=true;
//判断左右是不是平衡,判断左右的高度差是否大于1
if(!leftInfo.IsBalanced||!rightInfo.IsBalanced||Math.abs(leftInfo.height-rightInfo.height)>1){
IsBalanced=false;
}
return new Info(IsBalanced, height);
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.right.left = new Node(5);
head.right.right = new Node(6);
head.left.left.right = new Node(7);
System.out.println(process1(head));
}
}
/*false
1
2 3
4 5 6
7
判断满二叉树
给定一个二叉树的头结点,返回这个二叉树是不是满二叉树
特点:2^L-1=N
思路和上述的判断平衡二叉树大致一致
package BinaryTree;
public class IsFull {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static boolean process1(Node head){
if (head==null) {
return true;
}
Info all=process(head);
return (1<<all.height)-1==all.nodes;
}
public static class Info{
public int nodes;
public int height;
public Info(int h,int n){
this.nodes=n;
height=h;
}
}
public static Info process(Node X){
if (X==null) {
return new Info(0, 0);
}
Info leftInfo=process(X.left);
Info rightInfo=process(X.right);
int height=Math.max(leftInfo.height, rightInfo.height)+1;//加的是头结点的高度
int nodes=leftInfo.nodes+rightInfo.nodes+1;
return new Info(height, nodes);
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.right.left = new Node(5);
head.right.right = new Node(6);
head.left.left.right = new Node(7);
System.out.println(process1(head));
}
}
//false
判断完全二叉树
给定一个二叉树的头节点,返回这个二叉树是不是完全二叉树
完全二叉树特点:
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
非递归思想:
1)任何节点有右无左,false,否则继续
2)一旦遇到左右孩子不双全的,后续遇到的所有节点必须为叶子节点
package BinaryTree;
import java.util.LinkedList;
public class IsCBT {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static boolean isBCT(Node head){
if (head==null) {
return true;
}
LinkedList< Node> queue=new LinkedList<>();
//是否遇到过左右两个孩子不双全的节点
boolean leaf=false;
Node Left=null;
Node Right=null;
queue.add(head);
while(!queue.isEmpty()){
head=queue.poll();
Left=head.left;
Right=head.right;
//如果遇到了不双全的节点之后,又发现当前节点不是叶子节点,也就是左右结点还有孩子,不管是左边,还是右边
if (
(leaf&&(Left!=null && Right!=null))
||
//如果左树没有节点,右树有节点,即不是满二叉树
(Left==null&& Right!=null)
) {
return false;
}
if (Left!=null) {
queue.add(Left);
}
if (Right!=null) {
queue.add(Right);
}
//左右孩子有一个缺失,就认为左右孩子不双全
if (Left==null||Right==null) {
leaf=true;
}
}
return true;
}
public static void main(String[] args) {
Node head = new Node(0);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
System.out.println(isBCT(head));
}
}
//false
递归思想:
1)左右都是满二叉树,无缺口
2)左树是完全二叉树,右树是满二叉树,且左树的高度比右树高1
3)左树是满二叉树,右树是满二叉树,且左树的高度比右树高1
4)左树是满二叉树,右树是完全二叉树,并且它们高度一样
package BinaryTree;
public class IsCBT1 {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
//对于每一颗树,是否是满二叉树,是否是完全二叉树,高度
public static class Info{
public boolean Isfull;
public boolean isCBT;
public int height;
public Info(boolean f,boolean c,int h){
this.Isfull=f;
this.isCBT=c;
this.height=h;
}
}
public static boolean isCBT2(Node head) {
if (head == null) {
return true;
}
return process(head).isCBT;
}
public static Info process(Node head){
if (head==null) {
return new Info(true,true,0);
}
Info leftInfo=process(head.left);
Info rightInfo=process(head.right);
int height=Math.max(leftInfo.height, rightInfo.height)+1;
boolean isfull=leftInfo.Isfull&& rightInfo.Isfull&&(leftInfo.height==rightInfo.height);
boolean isCBT=false;
if (isfull) {
isCBT=true;
}else {//以x为头的整棵树,不满
if (leftInfo.isCBT&& rightInfo.isCBT) {
if (leftInfo.Isfull && rightInfo.isCBT && leftInfo.height==rightInfo.height+1) {
isCBT=true;
}
if (leftInfo.Isfull&& rightInfo.isCBT&& leftInfo.height==rightInfo.height+1) {
isCBT=true;
}
if (leftInfo.isCBT&& rightInfo.Isfull&& leftInfo.height==rightInfo.height) {
isCBT=true;
}
}
}
return new Info(isfull, isCBT, height);
}
public static void main(String[] args) {
Node head = new Node(0);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
System.out.println(isCBT2(head));
}
}
//false
用大量数据测试
package BinaryTree;
import java.util.LinkedList;
public class IsCBT2 {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static boolean isCBT1(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> queue = new LinkedList<>();
// 是否遇到过左右两个孩子不双全的节点
boolean leaf = false;
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
if (
// 如果遇到了不双全的节点之后,又发现当前节点不是叶节点
(leaf && (l != null || r != null))
||
(l == null && r != null)
) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if (l == null || r == null) {
leaf = true;
}
}
return true;
}
public static boolean isCBT2(Node head) {
if (head == null) {
return true;
}
return process(head).isCBT;
}
// 对每一棵子树,是否是满二叉树、是否是完全二叉树、高度
public static class Info {
public boolean isFull;
public boolean isCBT;
public int height;
public Info(boolean full, boolean cbt, int h) {
isFull = full;
isCBT = cbt;
height = h;
}
}
public static Info process(Node X) {
if (X == null) {
return new Info(true, true, 0);
}
Info leftInfo = process(X.left);
Info rightInfo = process(X.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean isFull = leftInfo.isFull
&&
rightInfo.isFull
&& leftInfo.height == rightInfo.height;
boolean isCBT = false;
if (isFull) {
isCBT = true;
} else { // 以x为头整棵树,不满
if (leftInfo.isCBT && rightInfo.isCBT) {
if (leftInfo.isCBT
&& rightInfo.isFull
&& leftInfo.height == rightInfo.height + 1) {
isCBT = true;
}
if (leftInfo.isFull
&&
rightInfo.isFull
&& leftInfo.height == rightInfo.height + 1) {
isCBT = true;
}
if (leftInfo.isFull
&& rightInfo.isCBT && leftInfo.height == rightInfo.height) {
isCBT = true;
}
}
}
return new Info(isFull, isCBT, height);
}
// for test
public static Node generateRandomBST(int maxLevel, int maxValue) {
return generate(1, maxLevel, maxValue);
}
// for test
public static Node generate(int level, int maxLevel, int maxValue) {
if (level > maxLevel || Math.random() < 0.5) {
return null;
}
Node head = new Node((int) (Math.random() * maxValue));
head.left = generate(level + 1, maxLevel, maxValue);
head.right = generate(level + 1, maxLevel, maxValue);
return head;
}
public static void main(String[] args) {
int maxLevel = 5;
int maxValue = 100;
int testTimes = 1000000;
for (int i = 0; i < testTimes; i++) {
Node head = generateRandomBST(maxLevel, maxValue);
if (isCBT1(head) != isCBT2(head)) {
System.out.println("Oops!");
}
}
System.out.println("finish!");
}
}
//finish!
二叉树最大距离
给定一颗二叉树的头节点head,任何两个结点之间都存在距离,返回整颗二叉树的最大距离
思路:
1)与X无关,要么是左树上面的最大距离,要么是右树上面的最大距离,用max函数取最大的
2)与X有关,X左树上面离自己最远的点,X右树上面离自己最远的点,左高+1+右高
package BinaryTree;
public class MaxDistance {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static int MaxDistance(Node head){
return process(head).maxdistance;
}
public static class Info{
public int maxdistance;
public int height;
public Info(int d,int h){
this.maxdistance=d;
this.height=h;
}
}
public static Info process(Node head){
if (head==null) {
return new Info(0,0);
}
Info leftInfo=process(head.left);
Info rightInfo=process(head.right);
int height=Math.max(leftInfo.height, rightInfo.height)+1;
int maxdistance=Math.max(
Math.max(leftInfo.maxdistance, rightInfo.maxdistance),
leftInfo.height+rightInfo.height+1);
return new Info(maxdistance, height);
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.right.left = new Node(5);
head.right.right = new Node(6);
head.left.left.right = new Node(7);
System.out.println(MaxDistance(head));
}
}
//6
最大的二叉搜索子树的头节点
给定一个二叉树的头节点head,返回这颗二叉树中最大的二叉搜索子树的大小
搜索二叉树:每个书上没有重复的值,左边的比我小,右边的比我大,每颗子树都是如此。
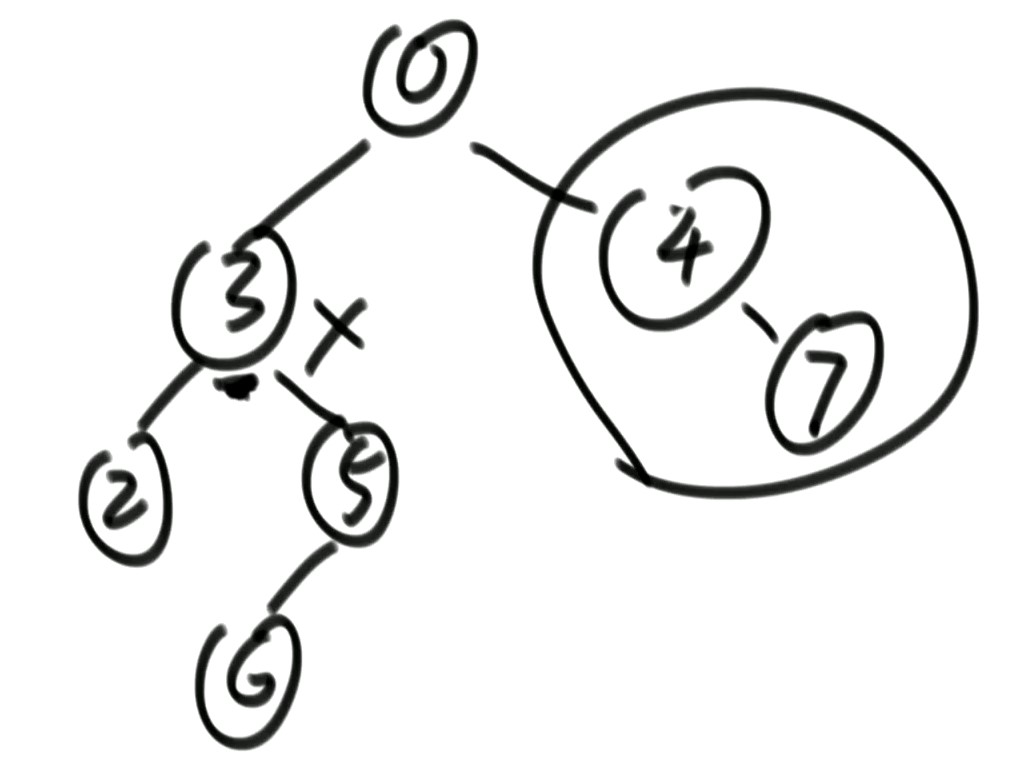
上图中,是搜索二叉树的为4,7。返回头节点,即为4
思路:
1)与X无关,左边最大的搜索二叉树,右边最大的搜索二叉树
2)与X有关,左右两边都是搜索二叉树,左边的max小于X,右边的min大于X
左右两边都需要:最大搜索子树的size,是否是搜索二叉树,最小值,最大值。
package BinaryTree;
public class MaxSubBSTSize {
public static class Node{
public int value;
public Node left;
public Node right;
public Node(int data){
this.value=data;
}
}
public static class Info{
public int maxsubBSTsize;
public boolean isAllBST;
public int max;
public int min;
public Info(boolean is,int maxsub,int max,int min){
this.isAllBST=is;
this.maxsubBSTsize=maxsub;
this.max=max;
this.min=min;
}
}
public static int maxSubBSTSize(Node head){
if (head==null) {
return 0;
}
return process(head).maxsubBSTsize;
}
public static Info process(Node head){
if (head==null) {
return null;
}
Info leftInfo=process(head.left);
Info rightInfo=process(head.right);
int max=head.value;
int min=head.value;
if (leftInfo!=null) {
max=Math.max(max, leftInfo.max);
min=Math.min(min, leftInfo.min);
}
if (rightInfo!=null) {
max=Math.max(max, rightInfo.max);
min=Math.min(min, rightInfo.min);
}
int maxsubBSTsize=0;
if (leftInfo!=null) {
maxsubBSTsize=leftInfo.maxsubBSTsize;
}
if (rightInfo!=null) {
maxsubBSTsize=Math.max(maxsubBSTsize, rightInfo.maxsubBSTsize);
}
boolean isAllBST=false;
if ( //左树。右树整体需要搜索二叉树
(leftInfo==null?true:leftInfo.isAllBST)
&&(rightInfo==null? true:rightInfo.isAllBST)
//左树最大值小于head,右树最小值大于head
&&(leftInfo==null?true:leftInfo.max<head.value)
&&(rightInfo==null?true:rightInfo.min>head.value)
) {
maxsubBSTsize=(leftInfo==null?0:leftInfo.maxsubBSTsize)+
(rightInfo==null? 0:rightInfo.maxsubBSTsize)+
1;
isAllBST=true;
}
return new Info(isAllBST, maxsubBSTsize, max, min);
}
public static void main(String[] args) {
Node head = new Node(0);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
System.out.println(maxSubBSTSize(head));
}
}
//2
最大的二叉搜索子树的头节点
给定一个二叉树的头节点head,返回这颗二叉树中最大的二叉搜索子树的头节点
package BinaryTree;
public class MaxSubBSTHead {
public static class Node{
public int value;
public Node left;
public Node right;
public Node(int data){
this.value=data;
}
//重写返回值
@Override
public String toString() {
return value +"";
}
}
public static class Info{
public int maxsubBSTsize;
public Node MaxSubBSTHead;
public int max;
public int min;
public Info(Node h,int maxsub,int max,int min){
this.MaxSubBSTHead=h;
this.maxsubBSTsize=maxsub;
this.max=max;
this.min=min;
}
}
public static Node MaxSubBSTHead(Node head){
if (head==null) {
return null;
}
return process(head).MaxSubBSTHead;
}
public static Info process(Node head){
if (head==null) {
return null;
}
Info leftInfo=process(head.left);
Info rightInfo=process(head.right);
int max=head.value;
int min=head.value;
Node MaxSubBSTHead=null;
int maxsubBSTsize=0;
if (leftInfo!=null) {
max=Math.max(max, leftInfo.max);
min=Math.min(min, leftInfo.min);
MaxSubBSTHead=leftInfo.MaxSubBSTHead;
maxsubBSTsize=leftInfo.maxsubBSTsize;
}
if (rightInfo!=null) {
max=Math.max(max, rightInfo.max);
min=Math.min(min, rightInfo.min);
if (rightInfo.maxsubBSTsize>maxsubBSTsize) {
MaxSubBSTHead=rightInfo.MaxSubBSTHead;
maxsubBSTsize=rightInfo.maxsubBSTsize;
}
}
if ((leftInfo==null?true:(leftInfo.MaxSubBSTHead==head.left && leftInfo.max<head.value))
&&(rightInfo==null ? true:(rightInfo.MaxSubBSTHead==head.right&& rightInfo.min>head.value))){
MaxSubBSTHead=head;
maxsubBSTsize=(leftInfo==null? 0:leftInfo.maxsubBSTsize)+
(rightInfo==null? 0:rightInfo.maxsubBSTsize)+1;
}
return new Info(MaxSubBSTHead, maxsubBSTsize, max, min);
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
System.out.println(MaxSubBSTHead(head));
}
}//4
最小公共祖先
题目:给定一个二叉树的头节点head,和另外两个节点a,b,返回a和b最小公共祖先。
无递归思想:
用一个map的value值表示父节点,并且用set值来表示o1的经过的父节点,从而判断o2与其的最小公共祖先。
package BinaryTree;
import java.util.HashMap;
import java.util.HashSet;
public class lowestAncestor {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
@Override
public String toString() {
return value +"";
}
}
public static Node lowestAncestor1(Node head,Node o1,Node o2){
if (head==null) {
return null;
}
//key的父节点是value
HashMap<Node, Node> ParentMap=new HashMap<>();
ParentMap.put(head, null);
fillParentMap(head, ParentMap);
HashSet<Node> o1Set=new HashSet<>();
Node cur=o1;
o1Set.add(cur);
//当父节点不为空,一直往上
while(ParentMap.get(cur)!=null){
cur=ParentMap.get(cur);
o1Set.add(cur);
}
cur=o2;
while(!o1Set.contains(cur)){
cur=ParentMap.get(cur);
}
return cur;
}
public static void fillParentMap(Node head,HashMap<Node, Node> ParentMap){
if (head.left!=null) {
ParentMap.put(head.left, head);
fillParentMap(head.left, ParentMap);
}
if (head.right!=null) {
ParentMap.put(head.right, head);
fillParentMap(head.right, ParentMap);
}
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
head.right.right.left=new Node(9);
System.out.println(lowestAncestor1(head,head.left.right.left,head.left.left));
}
}
//3
递归套路版:
思想:
1)o1,o2无一个在X上
2)o1,o2只有一个在X上
3)o1,o2都在X为头的树上
1:左右各一个
2:左o1,o2
3:右o1,o2
4:X是o1或者o2
package BinaryTree;
public class lowestAncestor1 {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
@Override
public String toString() {
return value +"";
}
}
public static Node lowestAncestor2(Node head,Node o1,Node o2){
return process2(head, o1, o2).ans;
}
public static class Info{
public Node ans;
public boolean findA;
public boolean findB;
public Info(Node ans,boolean a,boolean b){
this.ans=ans;
this.findA=a;
this.findB=b;
}
}
public static Info process2(Node head,Node o1,Node o2){
if (head==null) {
return new Info(null, false, false);
}
Info leftInfo=process2(head.left, o1, o2);
Info rightInfo=process2(head.right, o1, o2);
//要么是head等于o1,要么是左树上面找到o1,要么是右树上面找到o1;o2同理
boolean findA=head==o1||leftInfo.findA||rightInfo.findA;
boolean findB=head==o2||leftInfo.findB||rightInfo.findB;
//o1,o2最初的交汇点在哪里
//1:在左树上提前交汇了
//2:在右树上提前交汇了
Node ans=null;
if (leftInfo.ans!=null) {
ans=leftInfo.ans;
}
if (rightInfo.ans!=null) {
ans=rightInfo.ans;
}
if (ans==null) {
if (findA&&findB) {
ans=head;
}
}
return new Info(ans, findA, findB);
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(3);
head.right = new Node(4);
head.left.left = new Node(2);
head.left.right = new Node(5);
head.right.right = new Node(7);
head.left.right.left = new Node(6);
head.right.right.left=new Node(9);
System.out.println(lowestAncestor2(head,head.left.right.left,head.left.left));
}
}
//3
大量数据测试
package BinaryTree;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
public class lowestAncestor2 {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
@Override
public String toString() {
return value +"";
}
}
public static Node lowestAncestor1(Node head,Node o1,Node o2){
if (head==null) {
return null;
}
//key的父节点是value
HashMap<Node, Node> ParentMap=new HashMap<>();
ParentMap.put(head, null);
fillParentMap(head, ParentMap);
HashSet<Node> o1Set=new HashSet<>();
Node cur=o1;
o1Set.add(cur);
//当父节点不为空,一直往上
while(ParentMap.get(cur)!=null){
cur=ParentMap.get(cur);
o1Set.add(cur);
}
cur=o2;
while(!o1Set.contains(cur)){
cur=ParentMap.get(cur);
}
return cur;
}
public static void fillParentMap(Node head,HashMap<Node, Node> ParentMap){
if (head.left!=null) {
ParentMap.put(head.left, head);
fillParentMap(head.left, ParentMap);
}
if (head.right!=null) {
ParentMap.put(head.right, head);
fillParentMap(head.right, ParentMap);
}
}
public static Node lowestAncestor2(Node head,Node o1,Node o2){
return process2(head, o1, o2).ans;
}
public static class Info{
public Node ans;
public boolean findA;
public boolean findB;
public Info(Node ans,boolean a,boolean b){
this.ans=ans;
this.findA=a;
this.findB=b;
}
}
public static Info process2(Node head,Node o1,Node o2){
if (head==null) {
return new Info(null, false, false);
}
Info leftInfo=process2(head.left, o1, o2);
Info rightInfo=process2(head.right, o1, o2);
//要么是head等于o1,要么是左树上面找到o1,要么是右树上面找到o1;o2同理
boolean findA=head==o1||leftInfo.findA||rightInfo.findA;
boolean findB=head==o2||leftInfo.findB||rightInfo.findB;
Node ans=null;
if (leftInfo.ans!=null) {
ans=leftInfo.ans;
}
if (rightInfo.ans!=null) {
ans=rightInfo.ans;
}
if (ans==null) {
if (findA&&findB) {
ans=head;
}
}
return new Info(ans, findA, findB);
}
// for test
public static Node generateRandomBST(int maxLevel, int maxValue) {
return generate(1, maxLevel, maxValue);
}
// for test
public static Node generate(int level, int maxLevel, int maxValue) {
if (level > maxLevel || Math.random() < 0.5) {
return null;
}
Node head = new Node((int) (Math.random() * maxValue));
head.left = generate(level + 1, maxLevel, maxValue);
head.right = generate(level + 1, maxLevel, maxValue);
return head;
}
// for test
public static Node pickRandomOne(Node head) {
if (head == null) {
return null;
}
ArrayList<Node> arr = new ArrayList<>();
fillPrelist(head, arr);
int randomIndex = (int) (Math.random() * arr.size());
return arr.get(randomIndex);
}
// for test
public static void fillPrelist(Node head, ArrayList<Node> arr) {
if (head == null) {
return;
}
arr.add(head);
fillPrelist(head.left, arr);
fillPrelist(head.right, arr);
}
public static void main(String[] args) {
int maxLevel = 4;
int maxValue = 100;
int testTimes = 1000000;
for (int i = 0; i < testTimes; i++) {
Node head = generateRandomBST(maxLevel, maxValue);
Node o1 = pickRandomOne(head);
Node o2 = pickRandomOne(head);
if (lowestAncestor1(head, o1, o2) != lowestAncestor2(head, o1, o2)) {
System.out.println("Oops!");
}
}
System.out.println("finish!");
}
}
//finish!
派对的最大快乐值
题目:员工的信息定义如下
class Employee{
public int happy;//这名员工可以带来的快乐值
List<Employee>subordinates;//这名员工有哪些直接下级
}
公司的每个员工都符合Employee类的描述。整个公司的人员结构可以看作是一棵标准的、没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
x
a b c
1)X来,a.b.c不来情况下,a.b.c各自那棵树的最大值
2)X不来,max(a来,a不来),max(b来,b不来),max(c来,c不来)
两个信息:这个头节点在来的时候最大快乐值是多少,这个头节点在不来的时候最大快乐值是多少
暂时有问题
package BinaryTree;
import java.util.ArrayList;
public class MaxHappy {
public static class Employee{
public int happy;
public java.util.List<Employee> next;
public Employee(int h){
this.happy=h;
next=new ArrayList<>();
}
}
public static class Info{
public int yes;
public int no;
public Info(int y,int n){
this.yes=y;
this.no=n;
}
}
public static Info process(Employee head){
//没有直接下级
if (head.next.isEmpty()) {
return new Info(head.happy,0);
}
int yes=head.happy;
int no=0;
for (Employee next:head.next) {
Info nextInfo=process(next);
yes+=nextInfo.no;
no+=Math.max(nextInfo.yes,nextInfo.no);
}
return new Info(yes, no);
}
public static int way(Employee head){
Info allInfo=process(head);
return Math.max(allInfo.yes,allInfo.no);
}
public static void main(String[] args) {
Employee head=new Employee(1);
}
}
最后
以上就是外向发夹最近收集整理的关于二叉树的递归套路二叉树二又树的递归套路的全部内容,更多相关二叉树内容请搜索靠谱客的其他文章。






![[NOJ]数据结构 NO.16计算二叉树叶子节点数目[NOJ]数据结构 NO.16计算二叉树叶子节点数目](https://www.shuijiaxian.com/files_image/reation/bcimg5.png)

发表评论 取消回复