题目1：392.判断子序列

看到这一题最先想到的是双指针法，一个指向s、一个指向t，然后对比字符是否相等，如果相等i、j同时后移比较下一个字符，如果不相等j后移、i不变。

然后再结合昨天做的718、1143两道题的思路

1.确定dp数组以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

2.确定状态转移方程
s 、t 字符串各抽出一个前缀子字符串，判断s是否是t的子序列就是要在 t 中查找到 一个s：
如果末尾项一样，即s[i-1] == t[j-1]
以它们俩为末尾项的相同子序列长度取决于dp[i-1][j-1]能为它们俩提供多大的相同子序列长度然后加1，即dp[i][j] = dp[i-1][j-1] + 1;

如果末尾项不一样，即s[i-1] != t[j-1]
那么就将s的当前字符和t的下一个字符在进行比较，即dp[i][j]取决于s[i-1]与t[j-2]的比较结果，即dp[i][j] = dp[i][j-1];

3.dp数组初始化
如果 i== 0或j==0 ，即任意字符串为空，二者都没有公共部分，dp[i][j]=0

当dp[i][j]等于s的长度时，说明在t中找到了和s一样长度的子序列

4.确定遍历顺序
先遍历s字符串再遍历t字符串

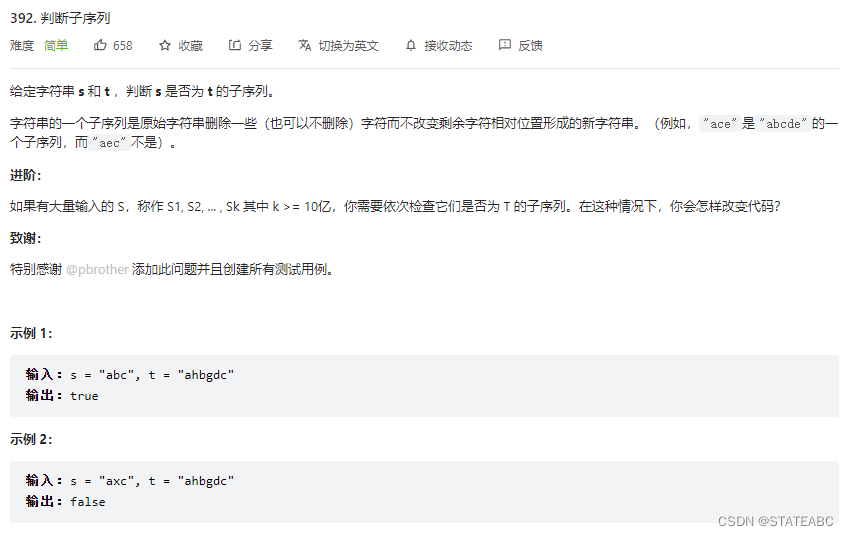
5.举例推导dp数组

题目2：115.不同的子序列

1.确定dp数组以及下标的含义
dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

2.确定状态转移方程
s 、t 字符串各抽出一个前缀子字符串：
如果末尾项一样，即s[i] == t[j]
如果 s[i-1]和 t[j-1] 匹配，则考虑 t[j-1] 作为 s[i-1] 的子序列，子序列个数为 dp[i-1][j-1]
如果 s[i-1] 不和 t[j-1] 匹配，则考虑 t[j-1] 作为 s[i-2] 的子序列，子序列个数为 dp[i-1][j]
综合以上两种情况：dp[i][j] = dp[i-1][j-1] + dp[i - 1][j]

如果末尾项不一样，即s[i] != t[j]
那么就将s的当前字符和t的下一个字符在进行匹配，即dp[i][j]取决于s[i-1]与t[j-2]的匹配结果，即dp[i][j] = dp[i-1][j];

3.dp数组初始化
如果 j = 0 即 t[j] 为空字符串，由于空字符串是任何字符串的子序列，因此对任意dp[i][0]=1；
如果 i = 0 即 s[i] 为空字符串，t[j] 为非空字符串，由于非空字符串不是空字符串的子序列，因此dp[0][j]=0。

4.确定遍历顺序
先遍历t字符串再遍历s字符串

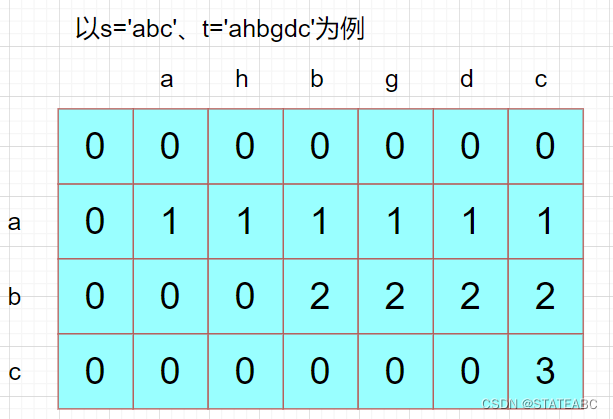
5.举例推导dp数组

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));  //dp数组类型为uint64_t是因为最后的结果会大于int型
        for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                else dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[s.size()][t.size()];
    }
};

题目3：583.两个字符串的删除操作

本题和1143.最长公共子序列基本相同，只需要求出两个字符串的最长公共子序列长度，然后将其它的字符全部删除，即用两个字符串的总长度减去最长公共子序列长度就是删除的步数

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));
        for (int i=1; i<=word1.size(); i++){
            for (int j=1; j<=word2.size(); j++){
                if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return word1.size()+word2.size()-dp[word1.size()][word2.size()]*2;
    }
};

当然也可以将1143.最长公共子序列的dp数组进行调整：
1.确定dp数组以及下标的含义
dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

2.确定状态转移方程
当word1[i - 1] 与 word2[j - 1]相同，就不要进行删除操作，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：
1.删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
2.删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
3.同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
取最小值，因此dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

3.dp数组初始化
dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除i个元素，才能和word2相同，即dp[i][0] = i。

dp[0][j]同理

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

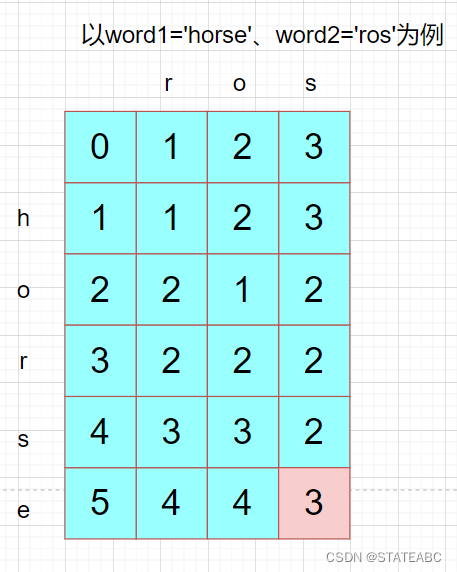
题目4：72.编辑距离

1.确定dp数组以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
2.确定状态转移方程
word1[i - 1] == word2[j - 1]，不需要任何操作，dp[i][j]=dp[i-1][j-1]

word1[i - 1] != word2[j - 1]，
如果word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作，即dp[i][j] = dp[i - 1][j] + 1;
如果word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作，即 dp[i][j] = dp[i][j - 1] + 1;
如果word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作，即 dp[i][j] = dp[i - 1][j - 1] + 1；
因此dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

注：word2添加一个元素，相当于word1删除一个元素

3.dp数组初始化
dp[i][0] = i，以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为i
dp[0][j]同理，dp[0][j] = j

4.确定遍历顺序
先遍历word1字符串再遍历word2字符串

5.举例推导dp数组

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = min({ dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1] }) + 1;
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

附上大佬很清晰的题解：编辑距离 | 图解DP | 最清晰易懂的讲解 【c++/java版本】

最后

以上就是清脆海燕为你收集整理的C++刷题笔记(42)——编辑距离、leetcode392、115、583、72题目1：392.判断子序列题目2：115.不同的子序列题目3：583.两个字符串的删除操作题目4：72.编辑距离的全部内容，希望文章能够帮你解决C++刷题笔记(42)——编辑距离、leetcode392、115、583、72题目1：392.判断子序列题目2：115.不同的子序列题目3：583.两个字符串的删除操作题目4：72.编辑距离所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。