上学期选了王老师的《现代信息检索》的课程,在“词典及容错式检索”中说到了编辑距离,计算编辑距离使用了动态规划的方法,感觉很有意思,于是实现了一下。
编辑距离的定义:
是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将akitten转成sitting:
kitten (a→ )
sitten (k→s)
sittin (e→i )
sitting (→g)
则编辑距离为4。
下面写出代码:

1 //Written by fangpei 2 //Find the editdistance between two strings, and print the steps of change 3 #include<iostream> 4 #include<string> 5 using namespace std; 6 7 int Min_m(int m0, int m1, int m2); 8 void Print_step(int m[][40][4], string s1, string s2, int len1, int len2); 9 10 int main() 11 { 12 string s1, s2; 13 cin >> s1 >> s2; 14 int i, j; 15 int len1 = s1.length(); 16 int len2 = s2.length(); 17 int m[40][40][4] = {0}; 18 for (i = 1; i <= len1; ++i) { 19 m[i][0][1] = i; 20 m[i][0][3] = i; 21 } 22 for (j = 1; j <= len2; ++j) { 23 m[0][j][2] = j; 24 m[0][j][3] = j; 25 } 26 for (i = 1; i <= len1; ++i) { 27 for (j = 1; j <= len2; ++j) { 28 if (s1[i-1] == s2[j-1]) 29 m[i][j][0] = m[i-1][j-1][3]; //copy(cost 0) 30 else 31 m[i][j][0] = m[i-1][j-1][3] + 1; //replace(cost 1) 32 m[i][j][1] = m[i-1][j][3] + 1; //delete(cost 1) 33 m[i][j][2] = m[i][j-1][3] + 1; //insert(cost 1) 34 // the least cost until this step 35 m[i][j][3] = Min_m(m[i][j][0], m[i][j][1], m[i][j][2]); 36 } 37 } 38 cout << m[len1][len2][3] << endl; 39 Print_step(m, s1, s2, len1, len2); 40 return 0; 41 } 42 43 int Min_m(int m0, int m1, int m2) //find the min of m[i][j][*] 44 { 45 if (m0 > m1) 46 m0 = m1; 47 if (m0 > m2) 48 return m2; 49 return m0; 50 } 51 52 //print the change step in detail 53 void Print_step(int m[][40][4], string s1, string s2, int len1, int len2) 54 { 55 while (len1 !=0 || len2 != 0) { 56 //copy(cost 0) 57 if (m[len1][len2][3] == m[len1][len2][0] && 58 m[len1][len2][0] == m[len1-1][len2-1][3]) { 59 cout << "copy '" << s1[len1-1] << "' to '" << 60 s2[len2-1] << "', cost 0" << endl; 61 --len1; 62 --len2; 63 } 64 //replace(cost 1) 65 else if (m[len1][len2][3] == m[len1][len2][0] && 66 m[len1][len2][0] == m[len1-1][len2-1][3] + 1) { 67 cout << "replace '" << s1[len1-1] << "' to '" << 68 s2[len2-1] << "', cost 1" << endl; 69 --len1; 70 --len2; 71 } 72 //delete(cost 1) 73 else if (m[len1][len2][3] == m[len1][len2][1] && m[len1][len2][1] != 0) { 74 cout << "delete '" << s1[len1-1] << "' to " << " * , cost 1" << endl; 75 --len1; 76 } 77 //insert(cost 1) 78 else if (m[len1][len2][3] == m[len1][len2][2] && m[len1][len2][2] != 0) { 79 cout << "insert * to '" << s2[len2-1] << "', cost 1" << endl; 80 --len2; 81 } 82 } 83 }

上面动态规划算法的步骤过程用矩阵来表达,比较对应的字符。
第一行和第一列:
都按照等差数列递增;(见下面的例子)
其余元素:
内部左上角数字:
如果行列对应的两个字符相等,则赋值为左上角元素的内部右下角数字的值;
如果行列对应的两个字符不相等,则赋值为左上角元素的内部右下角数字的值加1;
内部右上角数字:
赋值为上方元素的内部右下角数字加1;
内部左下角数字:
赋值为左方元素的内部右下角数字加1;
内部右下角数字:
赋值为内部另外三个数字的最小值。
最后求得的矩阵最右下角的数字为两个字符串的编辑距离。
详细的讲解参考《信息检索导论》(第5次印刷)第40页。
王老师讲的一个例子:
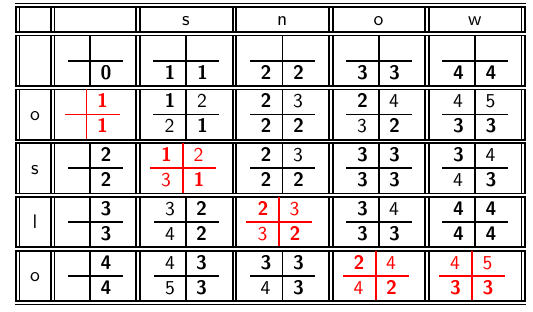
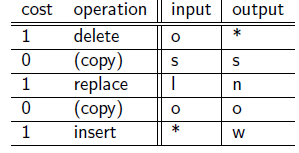
编辑距离变换步骤如下:
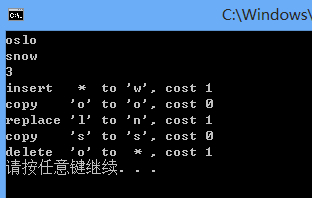
我的程序运行的结果(是上面变换步骤的倒序):
最后
以上就是细腻铃铛最近收集整理的关于编辑距离的计算和过程打印的全部内容,更多相关编辑距离内容请搜索靠谱客的其他文章。



![动态规划训练20 [Treats for the Cows POJ - 3186 ]](https://www.shuijiaxian.com/files_image/reation/bcimg4.png)



![[DP] Codeforces 403D #236 (Div. 1) D. Beautiful Pairs of Numbers](https://www.shuijiaxian.com/files_image/reation/bcimg8.png)
发表评论 取消回复