60 最大效益
作者: 朱星垠 时间限制: 10S章节: 二维数组
问题描述 :
明明的爸爸开了一家小公司，公司里有5名职员。今天，公司接待了5位客户。明明的爸爸知道，和任何一位客户谈判并签下合同都要花一整天的时间，而他又希望在一天之内，和这5位客户都签好合同。因此，明明的爸爸要求公司里的5名职员分别与1位客户谈判。
明明的爸爸也知道，这5名职员和5位客户的性格各不相同。因此，不同的职员与不同的客户谈判，会给公司带来不同的经济效益。他现在要做出一个决策，让5名职员分别与哪位客户谈判，才能让公司今天的总经济效益最大。
明明的爸爸首先做了一张5行5列的效益表，如下所示：
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
在这张效益表中，每行代表一名公司职员，每列代表一个客户，每行中的5个数字就表示了当该行所代表的公司职员和每位客户谈判时所能产生的效益。明明的爸爸就要通过这张效益表来决定哪位职员与哪位顾客谈判，然后能够使公司的效益最大。就拿上面这张表来看，由于无论哪位职员与哪位客户谈判，所产生的效益都是1，因此最大的效益就是5。这是最简单的一种情况，但是当效益表里的数字变得复杂，就很难进行选择，到底哪种组合方式才是最优的。因此明明的爸爸求助于你，帮助他解决这个问题。
明明的爸爸的问题可以归结为：给你一张5行5列的效益表，表中的数字均为大于等于0的整数，要求在这张表中选出5个数字，使这5个数字的和最大。（注：这5个数字分别来自表中的不同行不同列，即同一行只能选择一个数字，同一列也只能选择一个数字。）
输入说明 :
你写的程序要求从标准输入设备中读入测试数据作为你所写程序的输入数据。标准输入设备中有多组测试数据。每组测试数据占5行；每行包含5个正整数；第i行的第j个正整数Aij代表第i名职员与第j位客户谈判能为公司带来的经济效益（0≤Aij≤100,
1≤i,j≤5）。每组测试数据与其后一组测试数据之间没有任何空行；第一组测试数据前面以及最后一组测试数据后面也都没有任何空行。输出说明 :
对于每一组测试数据，你写的程序要求计算出一组相应的运算结果，并将每组运算结果作为你所写程序的输出数据依次写入到标准输出设备中。每组运算结果为一个整数s，即这一天中公司的最大可能总经济效益。例如：当测试数据中的所有Aij（1≤i,j≤5）均为1时，运算结果s应为5。输出时，每组运算结果s单独占一行，其行首和行尾都没有任何空格或其他任何字符；每组运算结果与其后一组运算结果之间没有任何空行或其他任何字符，第一组运算结果前面以及最后一组运算结果后面也都没有任何空行或其他任何字符。
注：通常，显示屏为标准输出设备。
输入范例 : 98 97 96 95 94 1 2 3 4 5 11 22 33 44 55 66 77 88 99 1 13 32
64 7 86 输出范例 : 318
用的递归，感觉思路没问题，不过输出有点奇怪……
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69/* T60 效益最大化 */ #include<stdio.h> #include<string.h> int flag[6];// flag[i]=1代表第i列已被选 int benefits[6][6] = { 0, 0, 0, 0, 0, 0, 0, 98, 97, 96, 95, 94, 0, 1, 2, 3, 4, 5, 0, 11, 22, 33, 44, 55, 0, 66, 77, 88, 99, 1, 0, 13, 32, 64, 7, 86};// 效益 int max;// 最大效益 void DFS(int row, int col, int curSum); int main() { int i = 0, j = 0; while (scanf("%d", &benefits[1][1]) != EOF) { max = 0; memset(flag, 0, sizeof(flag)); // for (i = 1; i <= 5; i++) { // for (j = 1; j <= 5; j++) { // if (!(i == 1 && j == 1)) // scanf("%d", &benefits[i][j]); // } // } for (i = 1; i <= 5; i++) { for (j = 1; j <= 5; j++) { printf("%d ", benefits[i][j]); } printf("n"); } DFS(0, 0, 0); printf("%dn", max); } return 0; } // 深度优先求最大效益 // row col 代表选中第几行第几列，curSum表示已累加的和 void DFS(int row, int col, int curSum) { int i = 0; printf("第%d行第%d列n", row, col); if (row == 5) {// 递归出口 if (curSum > max) { max = curSum; } flag[col] = 0;// 解除标记 } for (i = 1; i <= 5; i++) { if (flag[i] == 0) { flag[i] = 1;// 标记第i列已选 DFS(row + 1, i, curSum + benefits[row + 1][i]); flag[i] = 0;// 解除标记 } } }
输出：
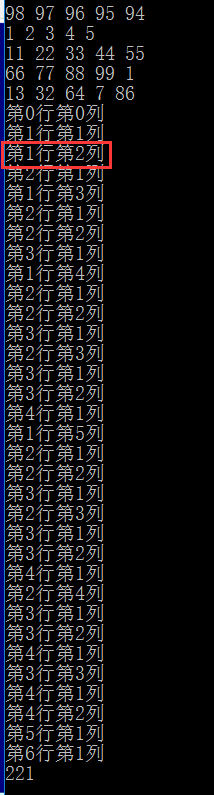
我寻思着这里输出个第一行什么鬼！？百思不得其解
害，不管递归了，试试五重循环吧
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74/* T60 效益最大化 */ #include<stdio.h> #include<string.h> int flag[6];// flag[i]=1代表第i列已被选 int benefits[6][6];// = { //0, 0, 0, 0, 0, 0, //0, 98, 97, 96, 95, 94, //0, 1, 2, 3, 4, 5, //0, 11, 22, 33, 44, 55, //0, 66, 77, 88, 99, 1, //0, 13, 32, 64, 7, 86};// 效益 int max;// 最大效益 void DFS(int row, int col, int curSum); int main() { int i = 0, j = 0, k = 0, l = 0, m = 0; int sum = 0; while (scanf("%d", &benefits[1][1]) != EOF) { max = 0; memset(flag, 0, sizeof(flag)); for (i = 1; i <= 5; i++) { for (j = 1; j <= 5; j++) { if (!(i == 1 && j == 1)) scanf("%d", &benefits[i][j]); } } // for (i = 1; i <= 5; i++) { // for (j = 1; j <= 5; j++) { // printf("%-4d", benefits[i][j]); // } // printf("n"); // } // DFS(0, 0, 0); for (i = 1; i <= 5 && !flag[i]; i++) { flag[i] = 1; for (j = 1; j <= 5 && !flag[j]; j++) { flag[j] = 1; for (k = 1; k <= 5 && !flag[k]; k++) { flag[k] = 1; for (l = 1; l <= 5 && !flag[l]; l++) { flag[l] = 1; for (m = 1; m <= 5 && !flag[m]; m++) { flag[m] = 1; sum = benefits[1][i] + benefits[2][j] + benefits[3][k] + benefits[4][l] + benefits[5][m]; if (sum > max) { max = sum; } flag[m] = 0; } flag[l] = 0; } flag[k] = 0; } flag[j] = 0; } flag[i] = 0; } printf("%dn", max); } return 0; }
为啥循环答案也不对？我的思路没错的呀
找了下，原来for循环里头条件判断（i <= 5 && !flag[i]）错了（虽然我也不知道为啥错了……），改了下总算AC了：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69/* T60 效益最大化 */ #include<stdio.h> #include<string.h> int flag[6];// flag[i]=1代表第i列已被选 int benefits[6][6];// 效益 int max;// 最大效益 void DFS(int row, int col, int curSum); int main() { int i = 0, j = 0, k = 0, l = 0, m = 0; int sum = 0; while (scanf("%d", &benefits[1][1]) != EOF) { max = 0, sum = 0; memset(flag, 0, sizeof(flag)); for (i = 1; i <= 5; i++) { for (j = 1; j <= 5; j++) { if (!(i == 1 && j == 1)) scanf("%d", &benefits[i][j]); } } for (i = 1; i <= 5; i++) { if (flag[i] != 0) continue; flag[i] = 1; for (j = 1; j <= 5; j++) { if (flag[j] != 0) continue; flag[j] = 1; for (k = 1; k <= 5; k++) { if (flag[k] != 0) continue; flag[k] = 1; for (l = 1; l <= 5; l++) { if (flag[l] != 0) continue; flag[l] = 1; for (m = 1; m <= 5; m++) { if (flag[m] != 0) continue; flag[m] = 1; sum = benefits[1][i] + benefits[2][j] + benefits[3][k] + benefits[4][l] + benefits[5][m]; if (sum > max) { max = sum; } flag[m] = 0; } flag[l] = 0; } flag[k] = 0; } flag[j] = 0; } flag[i] = 0; } printf("%dn", max); } return 0; }
还是想知道前面两种哪里有问题……
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
下面这种方法一位兄弟指出是错误的，我看了下确实是错的……
再更一种方法，不用五重循环的：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61/* T60 效益最大化 算法概述：每次从表中选一个最大的，然后把这个最大元素所在行和列上的所有元素 均置为-1，这样下一个最大元素就不可能跟上一个最大元素在同一行或者同一列了 */ #include<stdio.h> #include<string.h> int main() { int i = 0, j = 0; int max = 0, sum = 0; int flag = 0; int flagI = 0, flagJ = 0;// 记录最大元素所在坐标 int benefits[6][6]; while (scanf("%d", &benefits[1][1]) != EOF) { max = -1; sum = 0; for (i = 1; i <= 5; i++) { for (j = 1; j <= 5; j++) { if (!(i == 1 && j == 1)) scanf("%d", &benefits[i][j]); } } while (1) { flag = 0;// 默认没找到最大（全是-1） max = -1;// 每次找之前重置最大 for (i = 1; i <= 5; i++) {// 从所有数中找一个最大的 for (j = 1; j <= 5; j++) { if (benefits[i][j] > max) { flag = 1;// 表示有最大 flagI = i, flagJ = j; max = benefits[i][j]; } } } if (!flag) break; // 将当前最大元素所在行列的所有元素均置为-1 for (i = 1; i <= 5; i++) { benefits[i][flagJ] = -1; } for (i = 1; i <= 5; i++) { benefits[flagI][i] = -1; } sum += max; } printf("%dn", sum); } return 0; }
这个实际上是贪心的思想了，每次找当前最大。
从这个题我学到了：
- 一般来讲需要用多重循环的会有更好的方法解决
- 解决最大问题，多尝试用贪心，即每次找当前最佳
最后
以上就是朴素彩虹最近收集整理的关于东华oj-进阶题第60题-最大收益的全部内容，更多相关东华oj-进阶题第60题-最大收益内容请搜索靠谱客的其他文章。
![洛谷-【动态规划】- P2858 [USACO06FEB]奶牛零食Treats for the Cows](/uploads/reation/bcimg12.png)
发表评论 取消回复