过程

1、构造每一个自变量与其余自变量的线性回归模型，例如，数 据集中含有p个自变量，则第一个自变量与其余自变量的线性组合可以 表示为

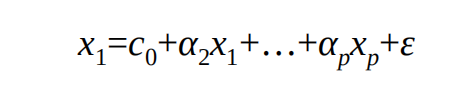
2、根据如上线性回归模型得到相应的判决系数，进而计算第 一个自变量的方差膨胀因子VIF：

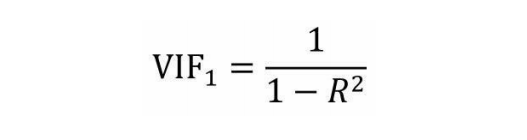
import pandas as pd
import numpy as np
from sklearn import model_selection
import statsmodels.api as sn
from statsmodels.stats.outliers_influence import variance_inflation_factor

sdata = pd.read_csv("…/input/traindatas/char7/Predict to Profit.csv")
print(sdata.columns)
X = sn.add_constant(sdata.loc[:,[‘RD_Spend’, ‘Marketing_Spend’]])
vif = pd.DataFrame()
vif[“Ficture”] = X.columns
vif[“Fctor”] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
print(vif)

执行结果如下，如上结果所示，两个自变量对应的方差膨胀因子均低于10，说明构 建模型的数据并不存在多重共线性。如果发现变量之间存在多重共线性 的话，可以考虑删除变量或者重新选择模型

Index(['RD_Spend', 'Administration', 'Marketing_Spend', 'State', 'Profit'], dtype='object')
           Ficture     Fctor
0            const  4.540984
1         RD_Spend  2.026141
2  Marketing_Spend  2.026141

过程计算

import pandas as pd
import numpy as np
from sklearn import model_selection
import statsmodels.api as sn
from statsmodels.stats.outliers_influence import variance_inflation_factor

sdata = pd.read_csv("…/input/traindatas/char7/Predict to Profit.csv")
model = sn.formula.ols(“RD_Spend~Marketing_Spend”,data=sdata).fit()
print(1/(1-model.rsquared))

执行结果

2.026140603233619

上面我仅仅计算了以RD_Spend为因变量计算的VIF值，和上面的一样，为2.026140603233619

最后

以上就是文艺绿草为你收集整理的方差膨胀因子过程过程计算的全部内容，希望文章能够帮你解决方差膨胀因子过程过程计算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。