1.题目：直方图中矩形的最大面积

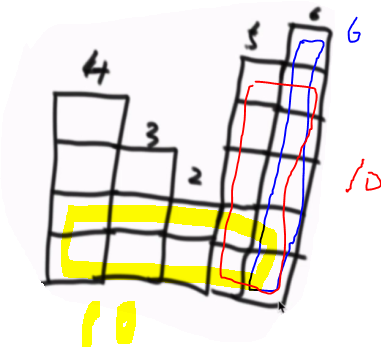
给定数组{ 6,5,2,3,4 }代表直方图的高度，求矩形的最大面积，如下图所示最大面积为红色或蓝色的10

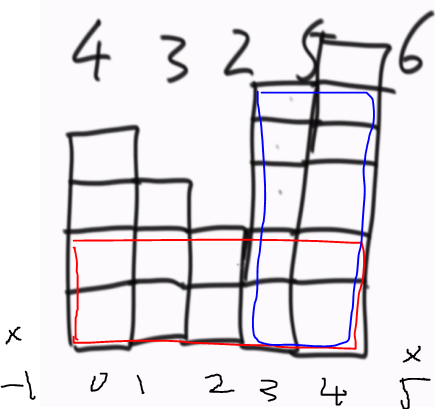
2.分析

本题可以把直方图的高视为一个杆子，杆子划过的距离的最大值为最大面积。如下图1长度为4的杆子只能在当前区域，右侧的高度为3小于4不能再向右滑动；而左侧位置越界。所以以4为高的杆子最大矩形为41 = 4。

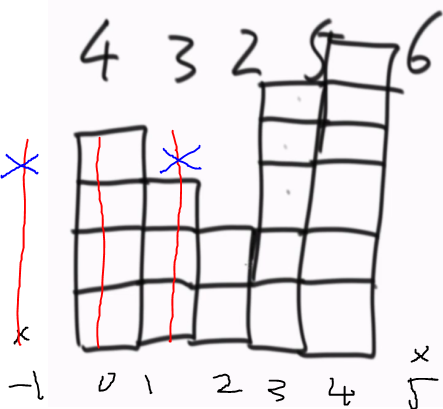
如下图2长度为3的杆子，右侧的长度为2小于3不能再向右滑动；而左侧位置可以滑动。所以以3为高的杆子最大矩形为32 = 6。

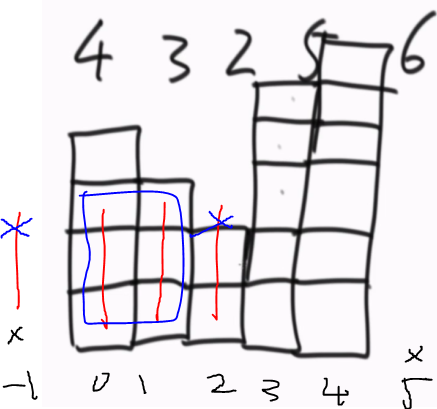
后面每个杆子左右滑动求出最大值就为矩形最大值。本题的杆子向右侧移动，如果碰到比他小的数就停下，所以是找到比他小的数。使用单调栈栈的底侧小顶部大。如果碰到栈中的数比当前大就出栈。

整个过程如下：
①把0位置的4放入栈中

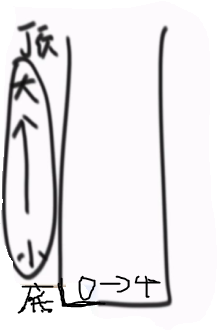
②1位置的3小于栈顶的4，表示杆子不能向右移，4需要弹出。结算4，在栈中4的底下没有数（表示左侧位置为-1越界），而4是由于新加入位置为1的3而弹出的，表示杆子的右侧是位置1，那么杆子实际扫过的的宽度为右侧位置减左侧位置再减一1-（-1）-1 = 1；好了，杆子高度为4的矩形面积为4* 1 = 4。3进栈。

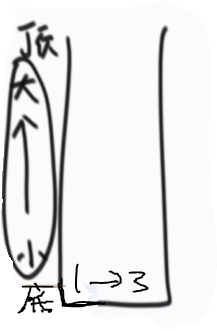
③同理高度为3的杆子大于高度为2杆子，3出栈，结算3，3的下面没有数，左侧为-1，右侧为新进来的2的位置为2，宽度为2-（-1）-1 = 2，所以面积为2*3 = 6。2进栈。

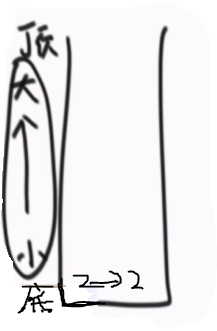
④下一个数为5,5比栈顶元素大，根据单调栈的要求，从下到上的数从小到大，所以可以进栈；同理6也进栈。

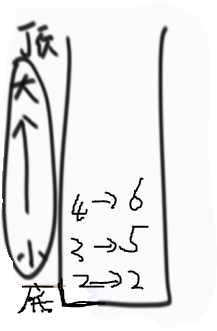
⑤由于遍历了整个数组。不会再有入栈操作，那么开始出栈，结算栈中的面积。
6首先出栈，进行结算，6出栈的原因不是别的数比他小而是后面没有数了，所以6的右侧为5（数组长度），左侧为6下面的数3，面积为（5-3-1）*6 = 6。对应在图中就是高度为6的矩形。
5再出栈，同理右侧为数组长度5，左侧为2，面积为（5-2-1）*5 = 10
2最后出栈，右侧为5，由于栈底为空，左侧为-1，面积是（5-（-1）-1）*2=10

3.核心代码

上面是整个流程，我们把他转化为代码，我们只把杆子的位置放进栈中，通过索引进行比较，而不是把杆子的高度放入。对于每个杆子，我们都需要进行计算，所以需要遍历整个数组，for (int i = 0; i < v.size(); i++)遍历的变量i表示当前杆子的位置。
只有在当前数小于栈顶的数时需要弹出结算while (!s.empty() && v[i] < v[s.top()])左侧位置引申为判断栈是否为空，为空左侧就是最左侧的-1位置，否则左侧就是它下面那个数的位置。右侧就是当前数i，那么杆子扫过的距离就是i - left - 1求出矩形面积并更新。再把当前位置入栈。

for (int i = 0; i < v.size(); i++)//遍历每个数
	{	//栈不空且当前高度小于栈中高度-->表示不能右扩需要弹出
		while (!s.empty() && v[i] < v[s.top()])
		{
			int cur = s.top();
			s.pop();
			int left = s.empty() ? -1 : s.top(); //left为左边界，若下面没有，是- 1，否则为下面的位置
			int curArea = (i - left - 1) * v[cur];;//i是右边界，i - left - 1是扩的格子长度
			maxArea = max(curArea,maxArea);
		}
		s.push(i);
	}

遍历完所有数后，对剩余的元素出栈。左侧位置依旧是下面的数，如果没有就是-1，而右侧位置变成了v.size()

while (!s.empty())
	{
		int cur = s.top();
		s.pop();
		int left = s.empty() ? -1 : s.top();
		int curArea = (v.size() - left - 1) * v[cur];
		maxArea = max(curArea, maxArea);
	}

4.完整代码

#include<iostream>
#include<stack>
#include<vector>
#include<algorithm>
using namespace std;
//单调栈，从底到顶从小到大
int maxRecFromBottom(vector<int>& v)
{
	if (v.empty())	return 0;
	stack<int> s;
	int maxArea = 0;
	for (int i = 0; i < v.size(); i++)//遍历每个数
	{	//栈不空且当前高度小于栈中高度-->表示不能右扩需要弹出
		while (!s.empty() && v[i] < v[s.top()])
		{
			int cur = s.top();
			s.pop();
			int left = s.empty() ? -1 : s.top(); //left为左边界，若下面没有，是- 1，否则为下面的位置
			int curArea = (i - left - 1) * v[cur];;//i是右边界，i - left - 1是扩的格子长度
			maxArea = max(curArea,maxArea);
		}
		s.push(i);
	}
	while (!s.empty())
	{
		int cur = s.top();
		s.pop();
		int left = s.empty() ? -1 : s.top();
		int curArea = (v.size() - left - 1) * v[cur];
		maxArea = max(curArea, maxArea);
	}
	return maxArea;
}
int main()
{
	//vector<int> v{4,3,2,5,6};
	vector<int> v{ 6,5,2,3,4 };
	cout << maxRecFromBottom(v);
	return 0;
}

最后

以上就是内向短靴为你收集整理的左神算法进阶class2—单调栈应用：直方图中矩形的最大面积1.题目：直方图中矩形的最大面积2.分析3.核心代码4.完整代码的全部内容，希望文章能够帮你解决左神算法进阶class2—单调栈应用：直方图中矩形的最大面积1.题目：直方图中矩形的最大面积2.分析3.核心代码4.完整代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。