CCF-CSP 201312-3 最大的矩形 (python)

问题描述

CCF-CSP 201312-3 最大的矩形

问题描述

  在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是hi。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

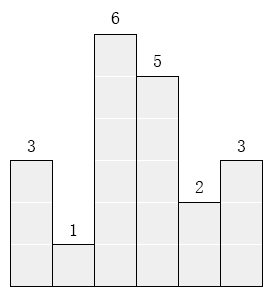
  请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。
　　

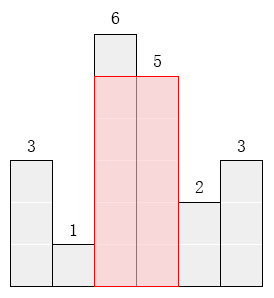
输入格式

  第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h1, h2, … , hn，相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。

输出格式

  输出一行，包含一个整数，即给定直方图内的最大矩形的面积。

样例输入

6
3 1 6 5 2 3

样例输出

10

思路1 分而治之

  脑中第一个浮现了分而治之的框架，试试就逝世。选择柱形图中最矮的那个柱子作为分界，左右两侧分别为子问题，在考虑跨分界线的情况时，矩形一定可以延伸至数列的两个边界。

解法1 分而治之

#input
n = eval(input())
line = input()
nums = [eval(num) for num in line.split()]
assert n == len(nums)
#print(nums)

# D & C algorithm
def findMaxArea(l,r):
    # conquer
    if l > r:
        return 0
    if l == r:
        return nums[l]
    
    # divide by the smallest number
    m = l
    minValue = nums[l]
    for i in range(l+1,r+1):
        if nums[i] < minValue:
            minValue = nums[i]
            m = i
    # merge
    maxL = findMaxArea(l,m-1)
    maxR = findMaxArea(m+1,r)
    maxC = minValue*(r-l+1)
    return max(maxL,max(maxR,maxC))

print(findMaxArea(0,n-1))

测评

CCF-CSP 90分，leetcode 84题超时。

复杂度分析

1. 平均时间复杂度为 O(nlogn)，最坏情况时间复杂度为 O(n²)。如果数组中的数字是有序的，分治算法将没有任何优化效果。
2. 空间复杂度为 O(n)。

  其实到这里可以发现思路1的缺点还是很明显的，divide的不均衡性可能导致在特殊的数据下超时。所以，如果真的要分而治之，还是老老实实等分，毕竟测评的数据往往是比较阴间的。

思路2 单调栈

  后续将更新关于单调栈的解法。leetcode 84的题解

最后

以上就是有魅力鲜花为你收集整理的CCF-CSP 201312-3 最大的矩形 (python)的全部内容，希望文章能够帮你解决CCF-CSP 201312-3 最大的矩形 (python)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。