前言碎碎念：秋招刷题中，整理一些系列题型。

经典例题

42. 接雨水

leetcode

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• $n==height.length$
• $1<=n<=2\ast 10^4$
• $0<=height[i]<=10^5$

思路

维持一个单调栈，栈内存储下标 $i$，下标所对应的高度 $height[i]$ 从栈顶到栈底递增，即栈顶的元素 $height[-1]$ 是最小的

分情况：

• 如果要入栈的元素 >= 栈顶：入栈
• 如果要入栈的元素 < 栈顶： 计算面积
  • 接水：栈顶（中间）+ 栈第二个元素（左）+ 要入栈
  • 
  • 
  • 
  • 

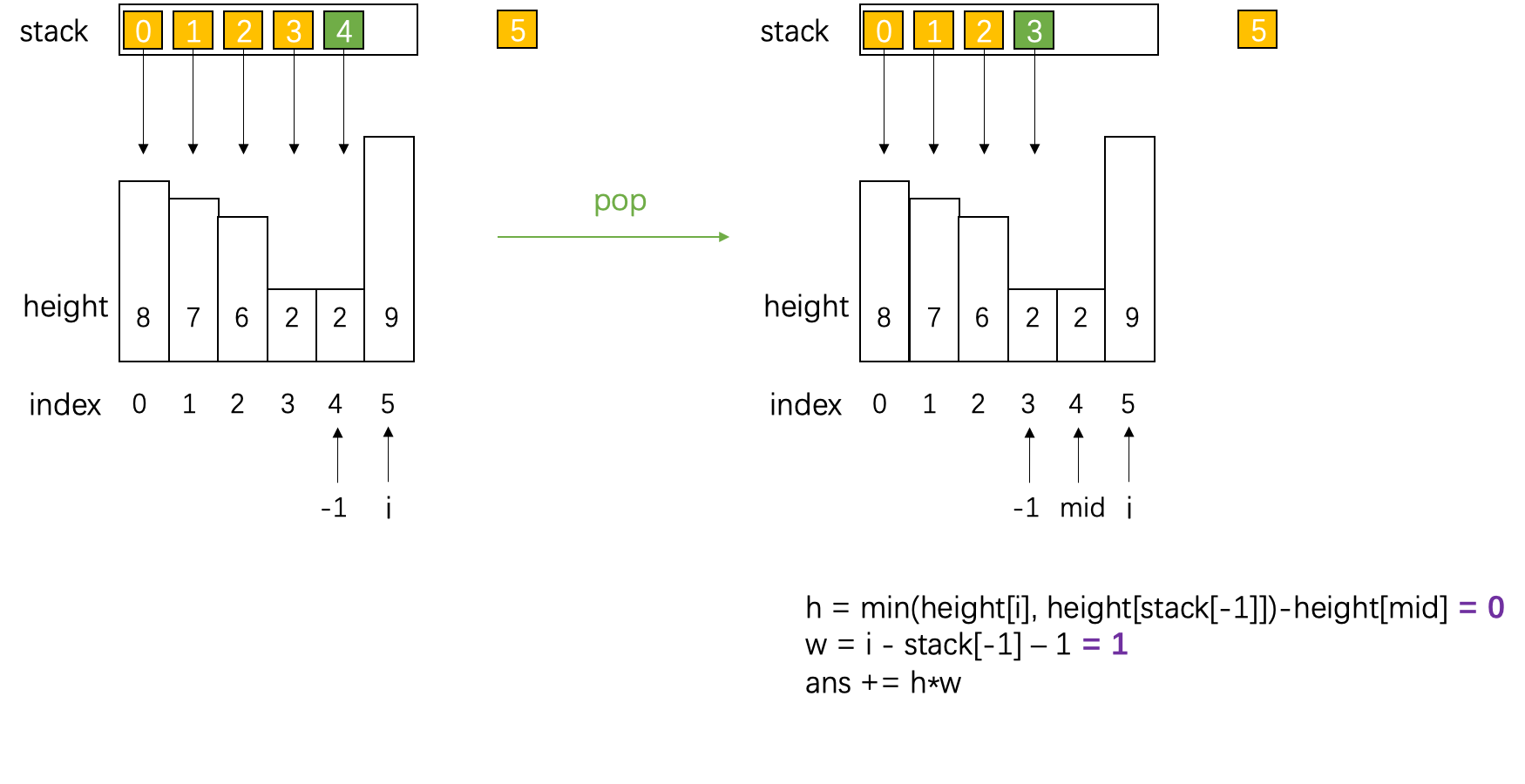
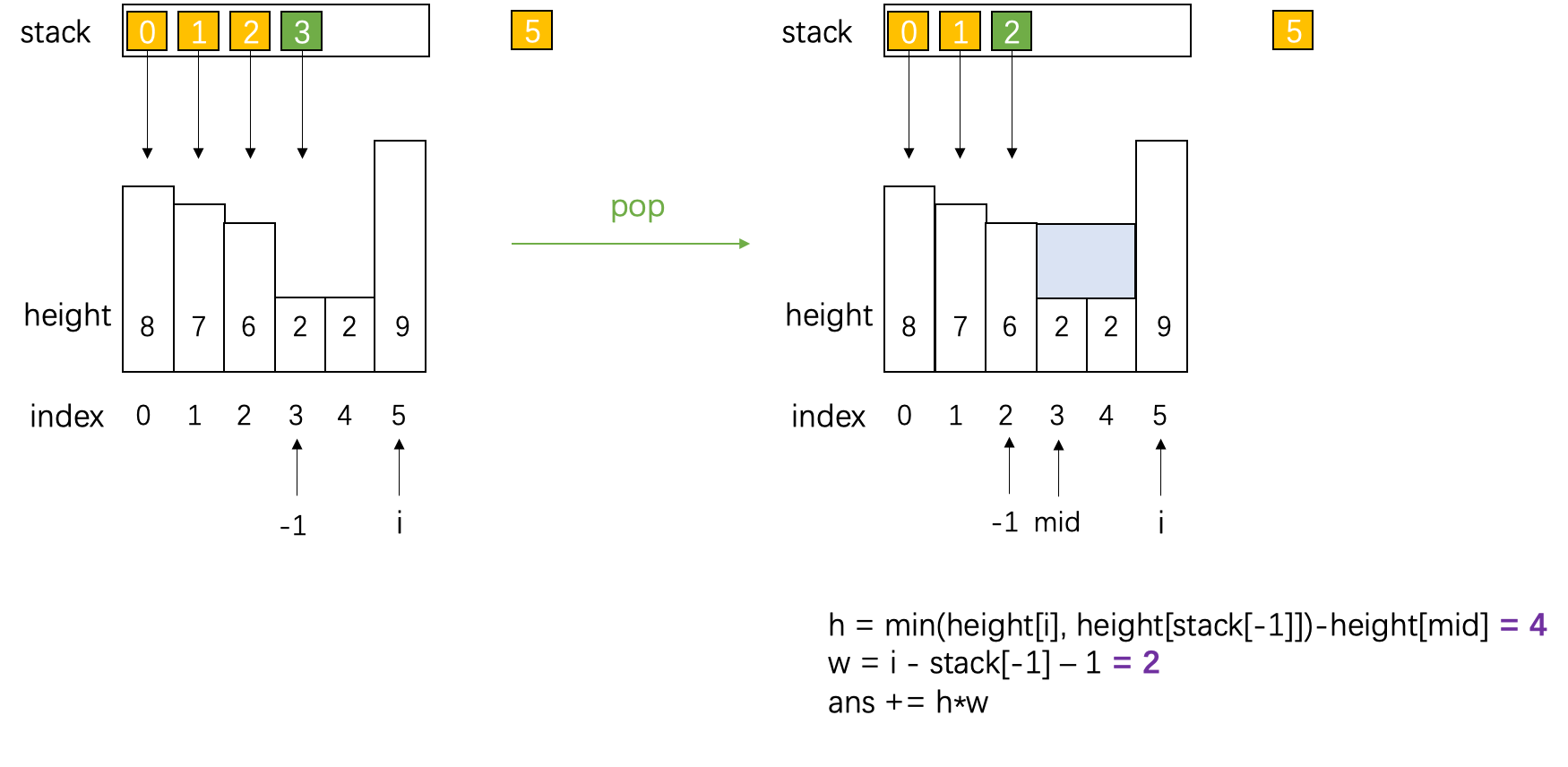
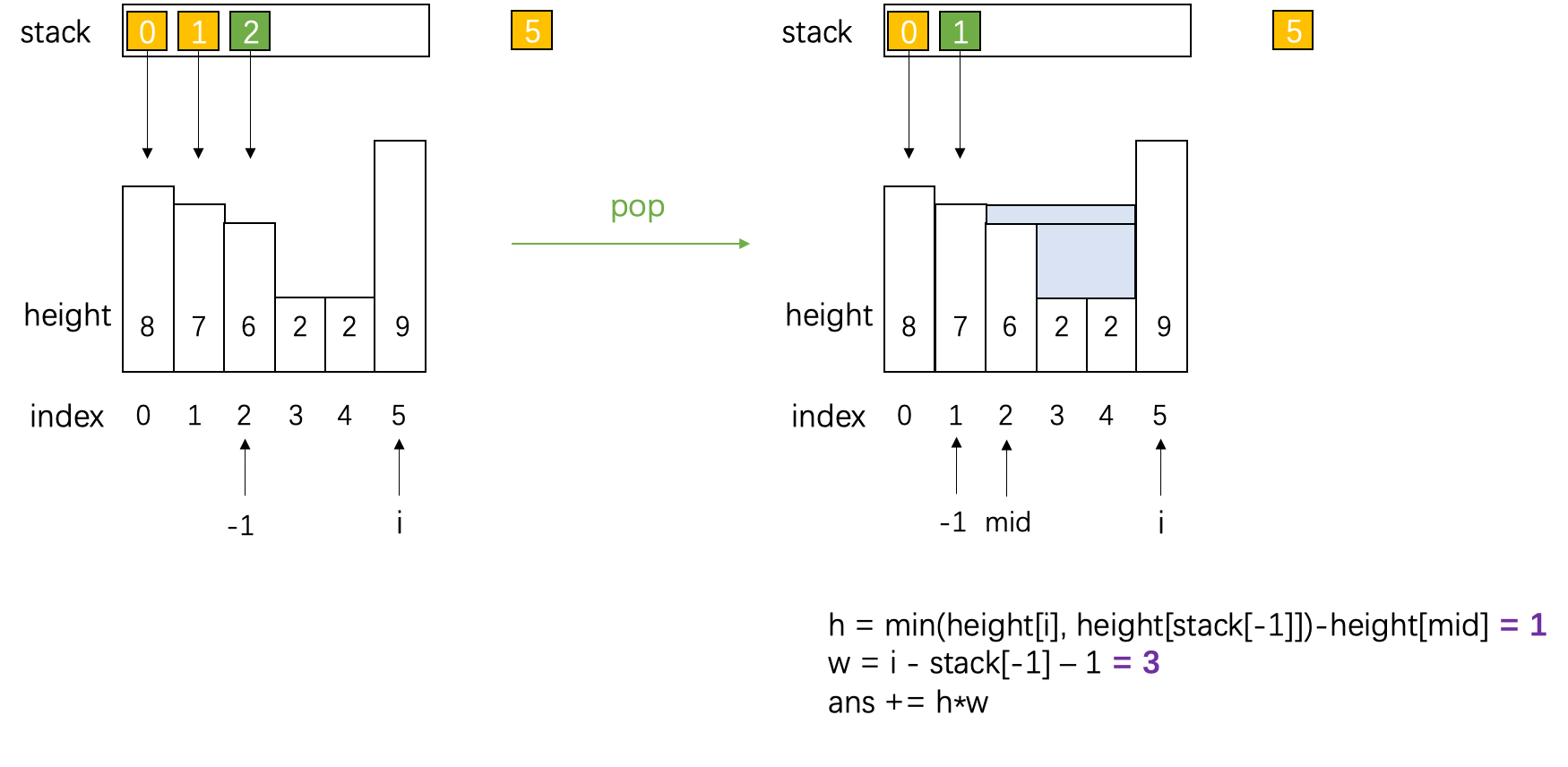
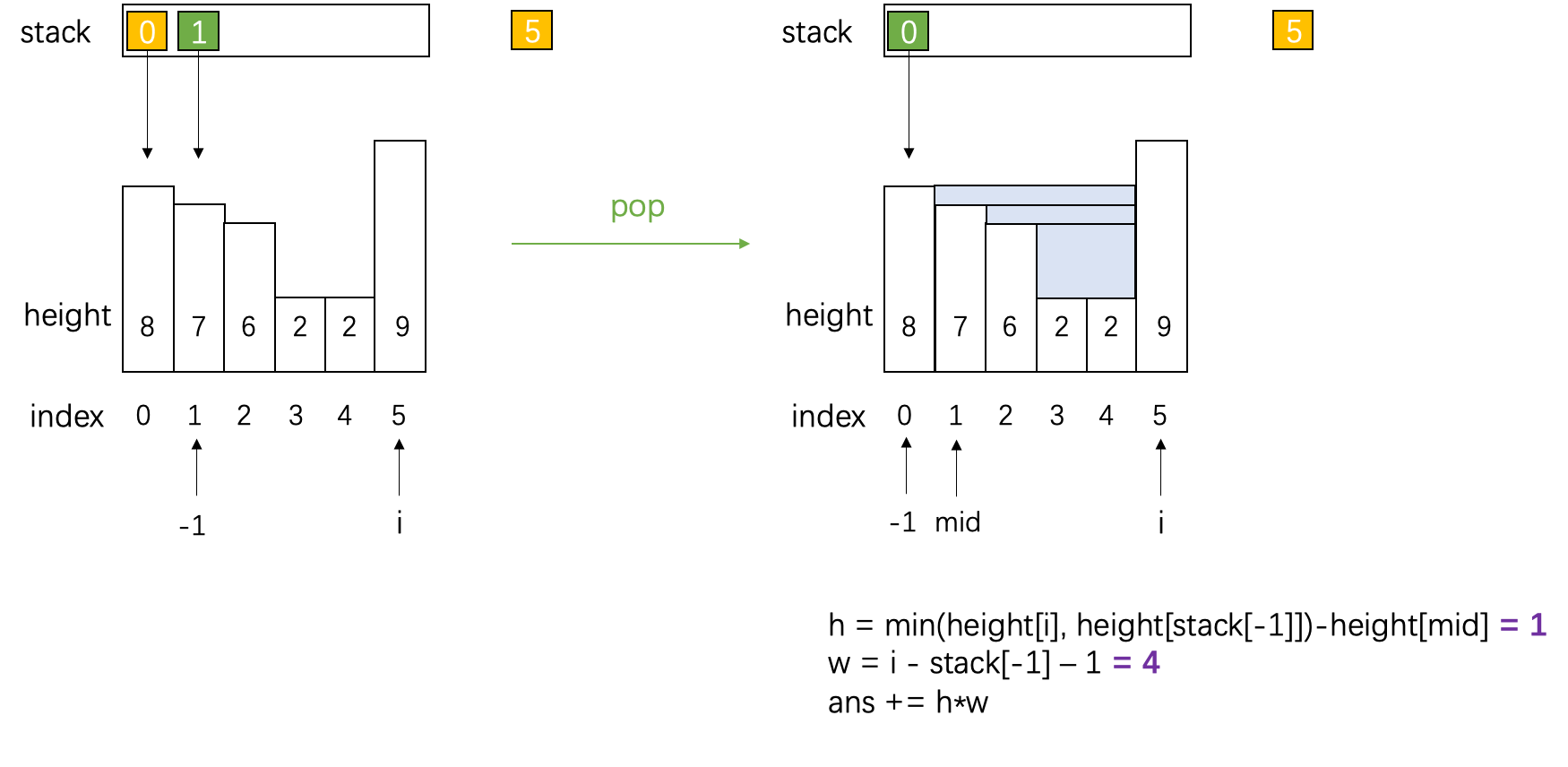
代码

class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        stack = []
        ans = 0

        for i in range(len(height)):
            # 计算面积
            while len(stack)>0 and height[i]>height[stack[-1]]:
                mid = stack[-1]
                stack.pop()
                if len(stack)>0:
                    h = min(height[i], height[stack[-1]])-height[mid]
                    w = i - stack[-1] - 1
                    ans += h*w

            stack.append(i)
        
        return ans

84. 柱状图中最大的矩形

leetcode

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

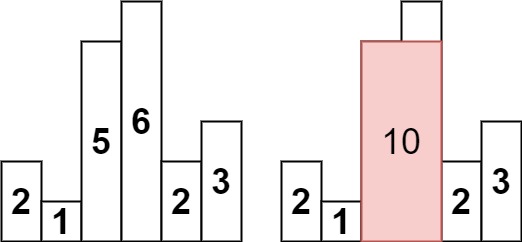
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

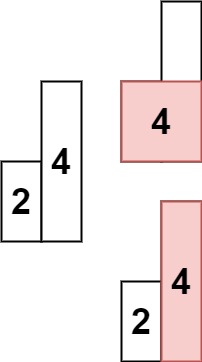
输入：heights = [2,4]
输出：4

提示：

• $1<=heights.length<=10^5$
• $0<=heights[i]<=10^4$

思路

单调栈 + 哨兵机制
存储下标

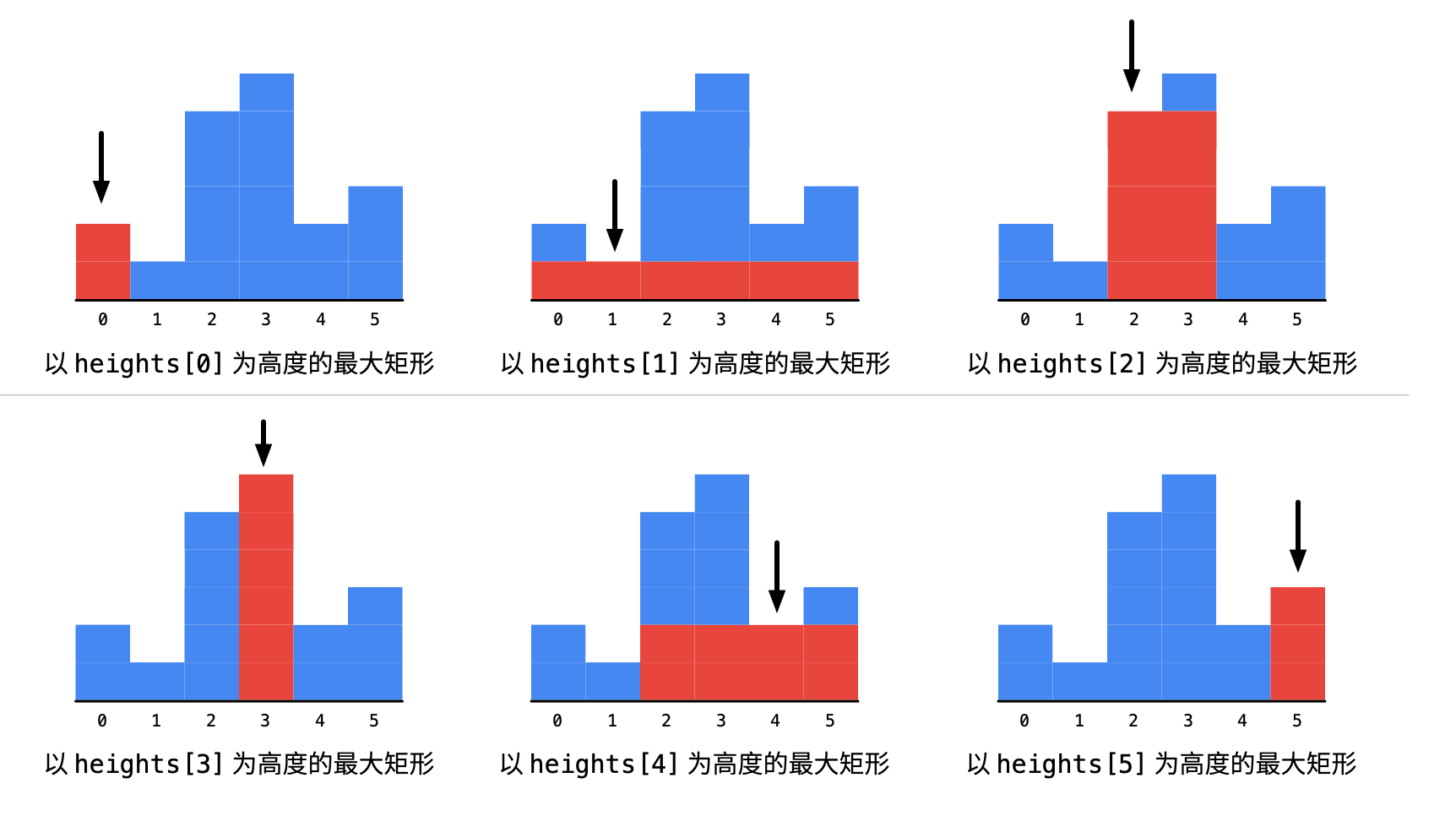
拿示例的数组 [2, 1, 5, 6, 2, 3] 为例：

1、一开始看到的柱形高度为 2 ，这个时候以这个 2 为高度的最大面积的矩形还不能确定，我们需要继续向右遍历，如下图。

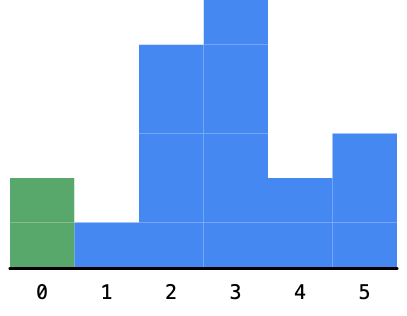
2、然后看到到高度为 1 的柱形，这个时候以这个柱形为高度的矩形的最大面积还是不知道的。但是它之前的以 2 为高度的最大面积的矩形是可以确定的，这是因为这个 1 比 2 小 ，因为这个 1 卡在了这里 2 不能再向右边扩展了，如下图。

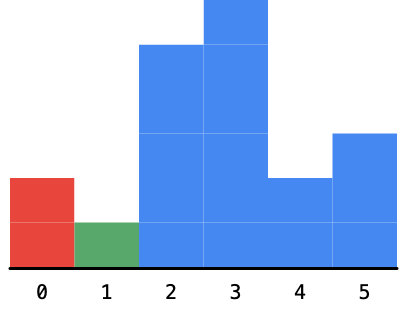
我们计算一下以 2 为高度的最大矩形的面积是 2。其实这个时候，求解这个问题的思路其实已经慢慢打开了。如果已经确定了一个柱形的高度，我们可以无视它，将它以虚框表示，如下图。

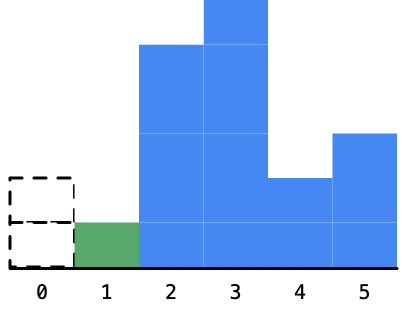
3、遍历到高度为 5 的柱形，同样的以当前看到柱形为高度的矩形的最大面积也是不知道的，因为我们还要看右边高度的情况。那么它的左右有没有可以确定的柱形呢？没有，这是因为 5 比 1 大，我们看后面马上就出现了 6，不管是 1 这个柱形还是 5 这个柱形，都还可以向右边扩展；

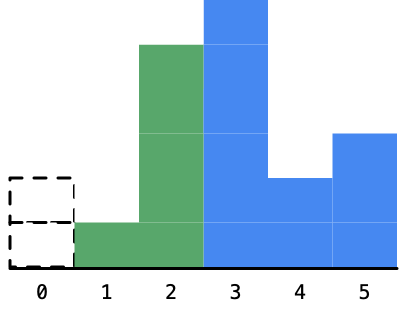
4、接下来，遍历到高度为 6 的柱形，同样的，以柱形 1、5、6 为高度的最大矩形面积还是不能确定下来；

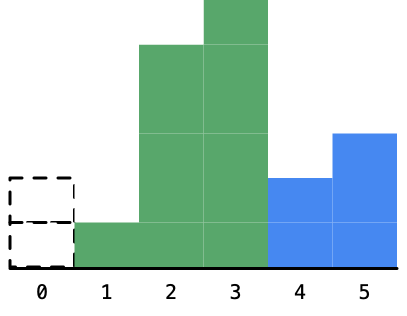
5、再接下来，遍历到高度为 2 的柱形。

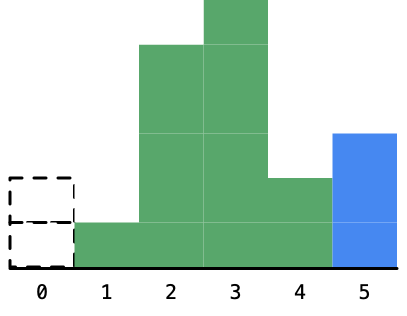
发现了一件很神奇的事情，高度为 6 的柱形对应的最大矩形的面积的宽度可以确定下来，它就是夹在高度为 5 的柱形和高度为 2 的柱形之间的距离，它的高度是 6，宽度是 1。

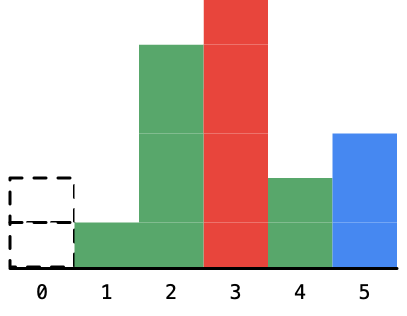
将可以确定的柱形设置为虚线。

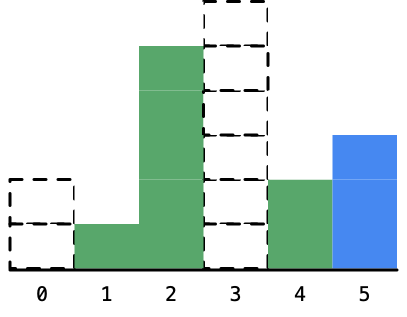
接下来柱形 5 对应的最大面积的矩形的宽度也可以确定下来，它是夹在高度为 1 和高度为 2 的两个柱形之间的距离；

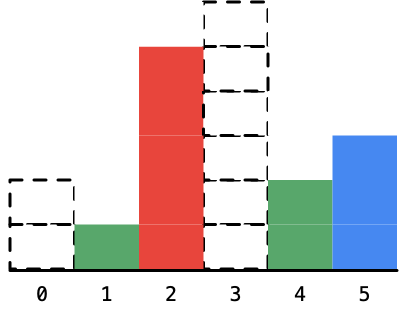
确定好以后，我们将它标成虚线。

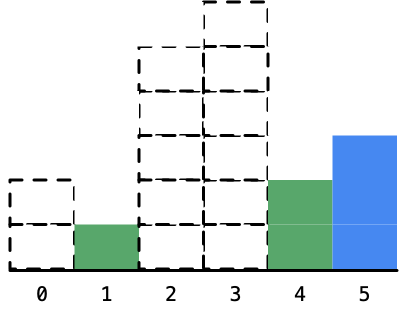
6、最后遍历到最后一个柱形，即高度为 3 的柱形。

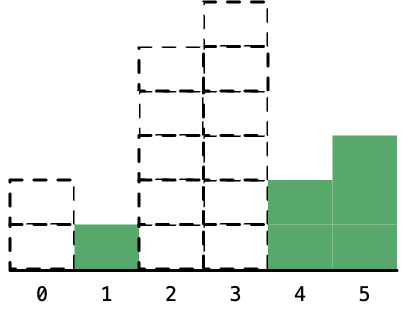
接下来我们就要依次考虑还在栈里的柱形的高度。和刚才的方法一样，只不过这个时候右边没有比它高度还小的柱形了，假设最右边还有一个下标为 len （这里等于 6） 的高度为 0 的柱形。

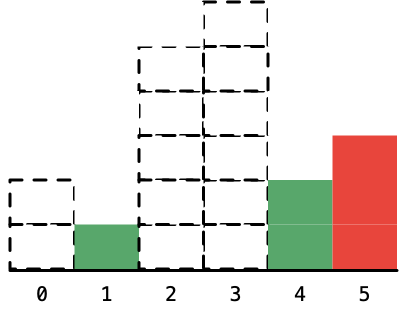
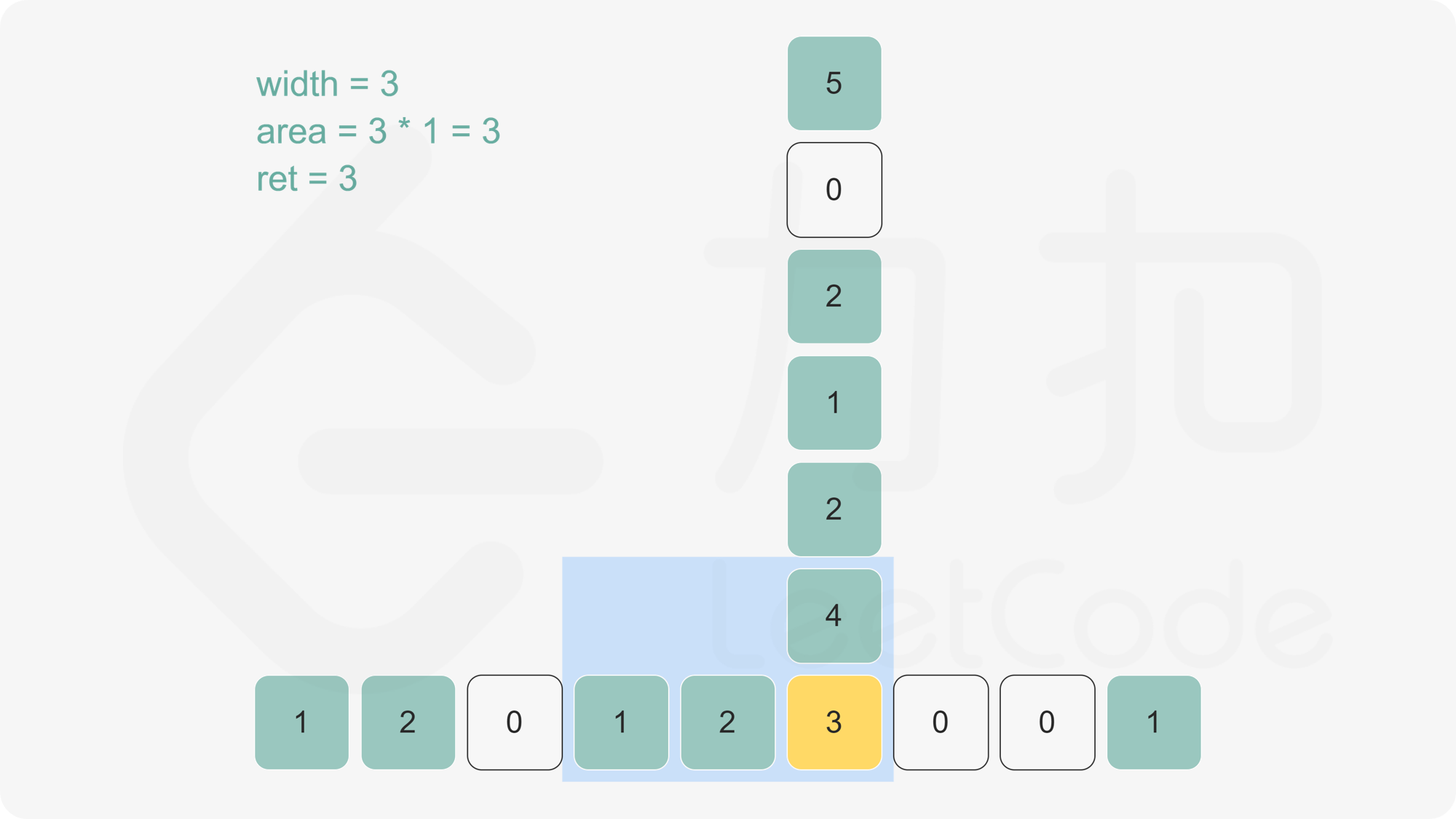
7、下标为 5 ，即高度为 3 的柱形，左边的下标是 4 ，右边的下标是 6 ，因此宽度是 6 - 4 - 1 = 1（两边都不算，只算中间的距离，所以减 1）；算完以后，将它标为虚线。

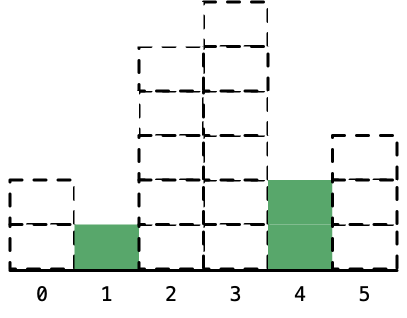
8、下标为 4 ，高度为 2 的柱形，左边的下标是 1 ，右边的下标是 6 ，因此宽度是 6 - 1 - 1 = 4；算完以后，将它标为虚线。

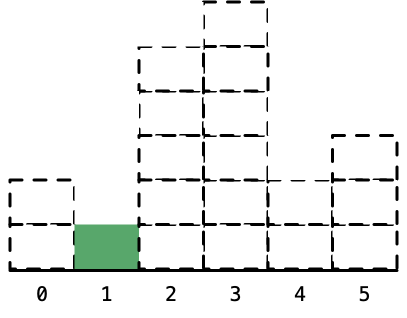
9、最后看下标为 1，高度为 1 的矩形，它的左边和右边其实都没有元素了，它就是整个柱形数组里高度最低的柱形，计算它的宽度，就是整个柱形数组的长度。

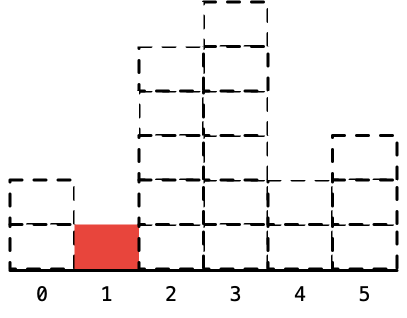
需要考虑两种特殊的情况：

1. 弹栈的时候，栈为空；
2. 遍历完成以后，栈中还有元素；

为此可以我们可以在输入数组的两端加上两个高度为 0 （或者是 0.5，只要比 1 严格小都行）的柱形，可以回避上面这两种分类讨论。

这两个站在两边的柱形有一个很形象的名词，叫做哨兵（Sentinel）。

有了这两个柱形：

• 左边的柱形（第 1 个柱形）由于它一定比输入数组里任何一个元素小，它肯定不会出栈，因此栈一定不会为空；

• 右边的柱形（第 2 个柱形）也正是因为它一定比输入数组里任何一个元素小，它会让所有输入数组里的元素出栈（第 1 个哨兵元素除外）。

代码

class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """
        ans = 0
        heights = [0] + heights + [0]          # 添加哨兵
        stack = [0]
        for i in range(1, len(heights)):       # 从 1 开始
            while heights[i] < heights[stack[-1]]:
                h = heights[stack.pop()]        # 要先pop出来，利用左边的下标
                w = i - stack[-1] - 1
                ans = max(ans, h*w)
                
            stack.append(i)
        
        return ans

85. 最大矩形

leetcode

题目

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

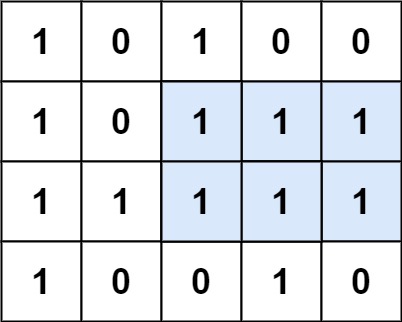
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0
 

提示：

• $rows==matrix.length$
• $cols==matrix[0].length$
• $1<=row,cols<=200$
• $matrix[i][j]{为}^{\prime }{0}^{\prime }{或}^{\prime }{1}^{\prime }$

思路

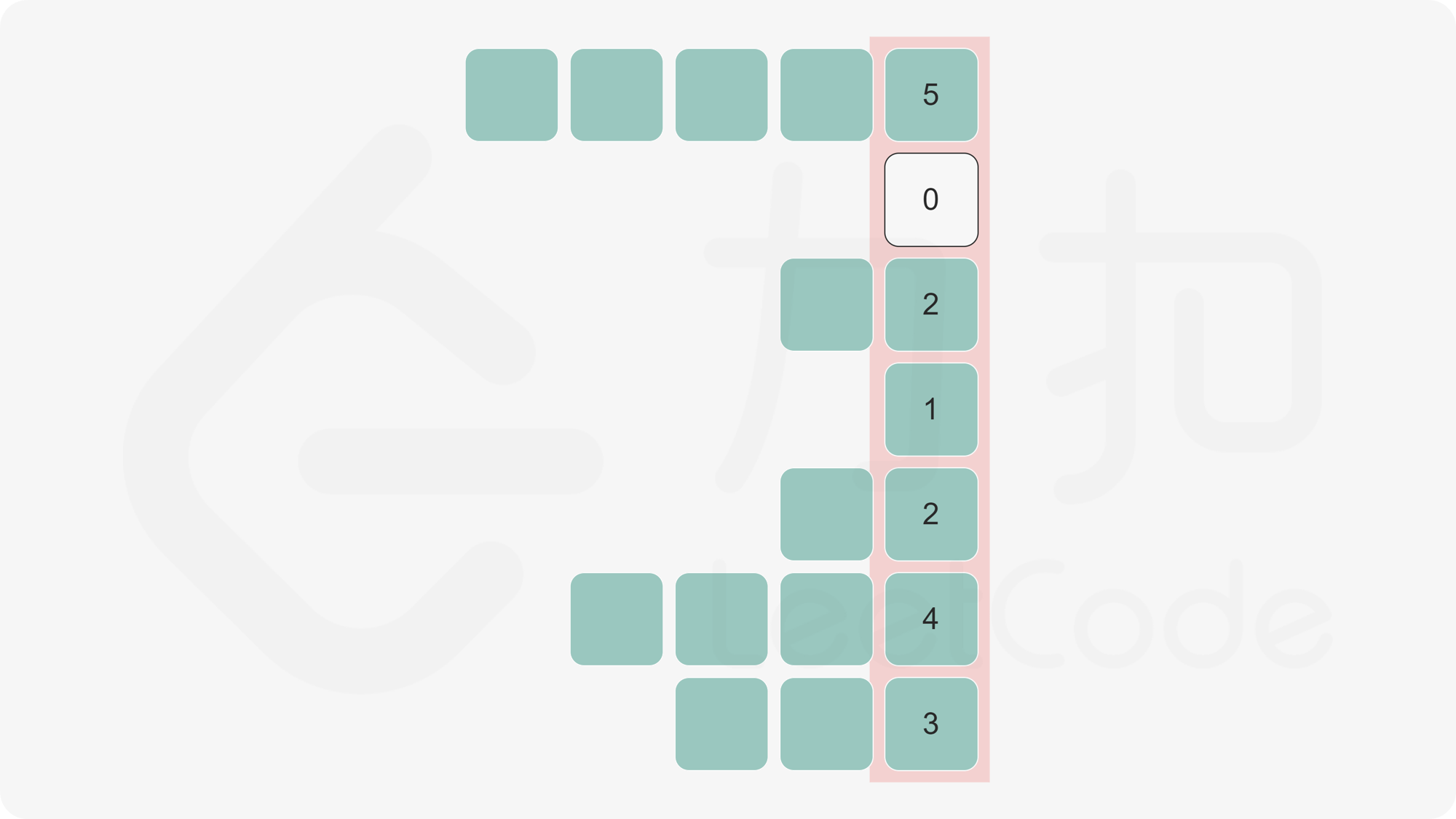
沿用上一题的思路，按照纵向，将每一列都变成柱状图，计算以右下角为矩形的面积

代码

class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        r, c = len(matrix), len(matrix[0])
        left = [[0]*c for _ in range(r+2)]      # 引入哨兵

        for i in range(r):
            for j in range(c):
                if matrix[i][j]=='1':
                    if j==0:
                        left[i+1][j] = 1
                    else:
                        left[i+1][j] = left[i+1][j-1] + 1
                else:
                    left[i+1][j] = 0
                    
        ans = 0
        for j in range(c):
            stack = [0]
            for i in range(1, r+2):
                while left[stack[-1]][j] > left[i][j]:
                    h = left[stack.pop()][j]
                    w = i - stack[-1] - 1
                    ans = max(ans, h*w)
                stack.append(i)
            
        return ans

参考资料

1. 暴力解法、栈（单调栈、哨兵技巧）
2. 最大矩形官方题解

最后

以上就是暴躁身影为你收集整理的leetcode刷题集：单调栈（python代码）经典例题参考资料的全部内容，希望文章能够帮你解决leetcode刷题集：单调栈（python代码）经典例题参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。