信息论基础（熵 联合熵 条件熵 信息增益 基尼不纯度）

熵

在引入熵的概念之前，思考一个问题， 抛硬币和投骰子，哪一个不确定性更强？直觉来说，投骰子的不确定性更强，因为有6中可能，而抛硬币只有两种可能（那种说中间的就别杠了）
Shannon提出了熵的概念，解决了以上这个问题。对于上述离散型随机事件，可以用离散熵定义其不确定性

log以2为底。

我们可以更进一步地看，一个随机变量的熵越大，意味着不确定性越大，那么也就是说，该随机变量包含的信息量越大，那到底信息量是什么呢？抛一枚硬币的信息量就是，正面朝上，反面朝上，这2就是信息量；同样，掷骰子的信息量就是6个不同数字的面朝上，这6也是信息量。那么，在计算机角度上看，熵到底是什么，在计算机中，要表示抛硬币的结果，需要用1 bit，要表示掷骰子的结果需要用log6 bit（实际表示时为向上取整3 bit），也就是说熵是平均意义上对随机变量的编码长度。

联合熵

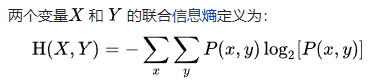
条件熵

信息增益

熵-条件熵 = 信息增益

基尼不纯度

从一个数据集中随机选取子项，度量其被错误的划分到其他组里的概率
fi为某概率事件发生的概率

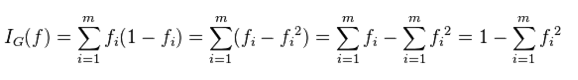
决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景

ID3算法

ID3算法才用信息增益来作为划分的依据， 就是朝着越不混乱的方向进行划分，就是信息增益最大的方向。

举例说明：

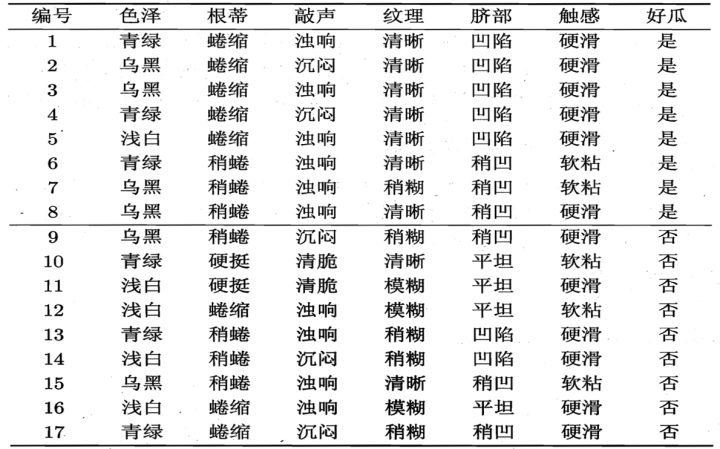
好瓜8/17, 不好瓜9/17， 熵为 -8/17 * log 8/17 - 9/17 * log 9/17 = 0.998
然后计算每个特征的信息增益

我们从上面求解信息增益的公式中，其实可以看出，信息增益准则其实是对可取值数目较多的属性有所偏好！
现在假如我们把数据集中的“编号”也作为一个候选划分属性。我们可以算出“编号”的信息增益是0.998
因为每一个样本的编号都是不同的（由于编号独特唯一，条件熵为0了，每一个结点中只有一类，纯度非常高啊），也就是说，来了一个预测样本，你只要告诉我编号，其它特征就没有用了，这样生成的决策树显然不具有泛化能力。 为了解决这个问题，就有了下面C4.5的算法

C4.5

这里我们引入信息增益率这个说法，定义如下


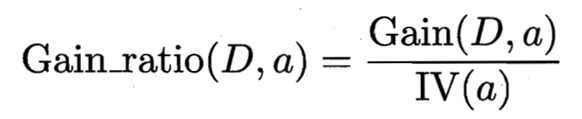
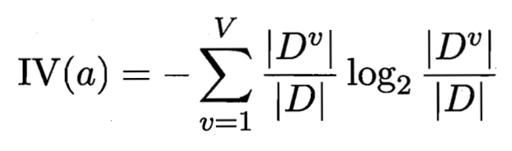
IV(触感) = 0.874 ( V = 2 )
IV(色泽) = 1.580 ( V = 3 )
IV(编号) = 4.088 ( V = 17 ）

C4.5算法不直接选择增益率最大的候选划分属性，候选划分属性中找出信息增益高于平均水平的属性（这样保证了大部分好的的特征），再从中选择增益率最高的（又保证了不会出现编号特征这种极端的情况）

CART分类树

CART：classification and regression tree. 这是一个二叉树。
CART中用于选择变量的不纯性度量是Gini指数；
如果目标变量是标称的，并且是具有两个以上的类别，则CART可能考虑将目标类别合并成两个超类别（双化）；
如果目标变量是连续的，则CART算法找出一组基于树的回归方程来预测目标变量。

CART分类树预测分类离散型数据，采用基尼指数选择最优特征，同时决定该特征的最优二值切分点。分类过程中，假设有K个类，样本点属于第k个类的概率为Pk，则概率分布的基尼指数定义为

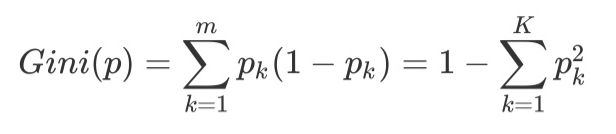
根据基尼指数定义，可以得到样本集合D的基尼指数，其中Ck表示数据集D中属于第k类的样本子集。

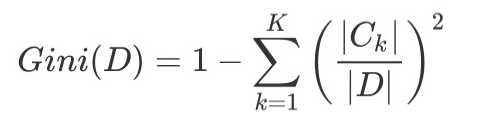
如果数据集D根据特征A在某一取值a上进行分割，得到D1,D2两部分后，那么在特征A下集合D的基尼系数如下所示。其中基尼系数Gini(D)表示集合D的不确定性，基尼系数Gini(D,A)表示A=a分割后集合D的不确定性。基尼指数越大，样本集合的不确定性越大。

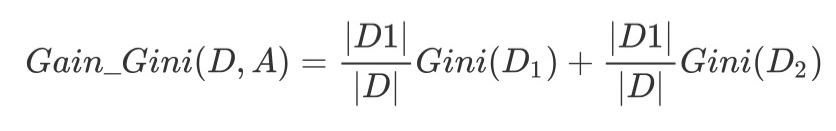
对于属性A，分别计算任意属性值将数据集划分为两部分之后的Gain_Gini，选取其中的最小值，作为属性A得到的最优二分方案。然后对于训练集S，计算所有属性的最优二分方案，选取其中的最小值，作为样本及S的最优二分方案。

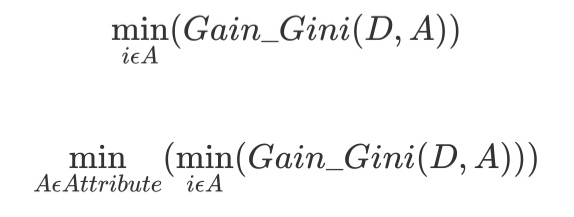
举个例子

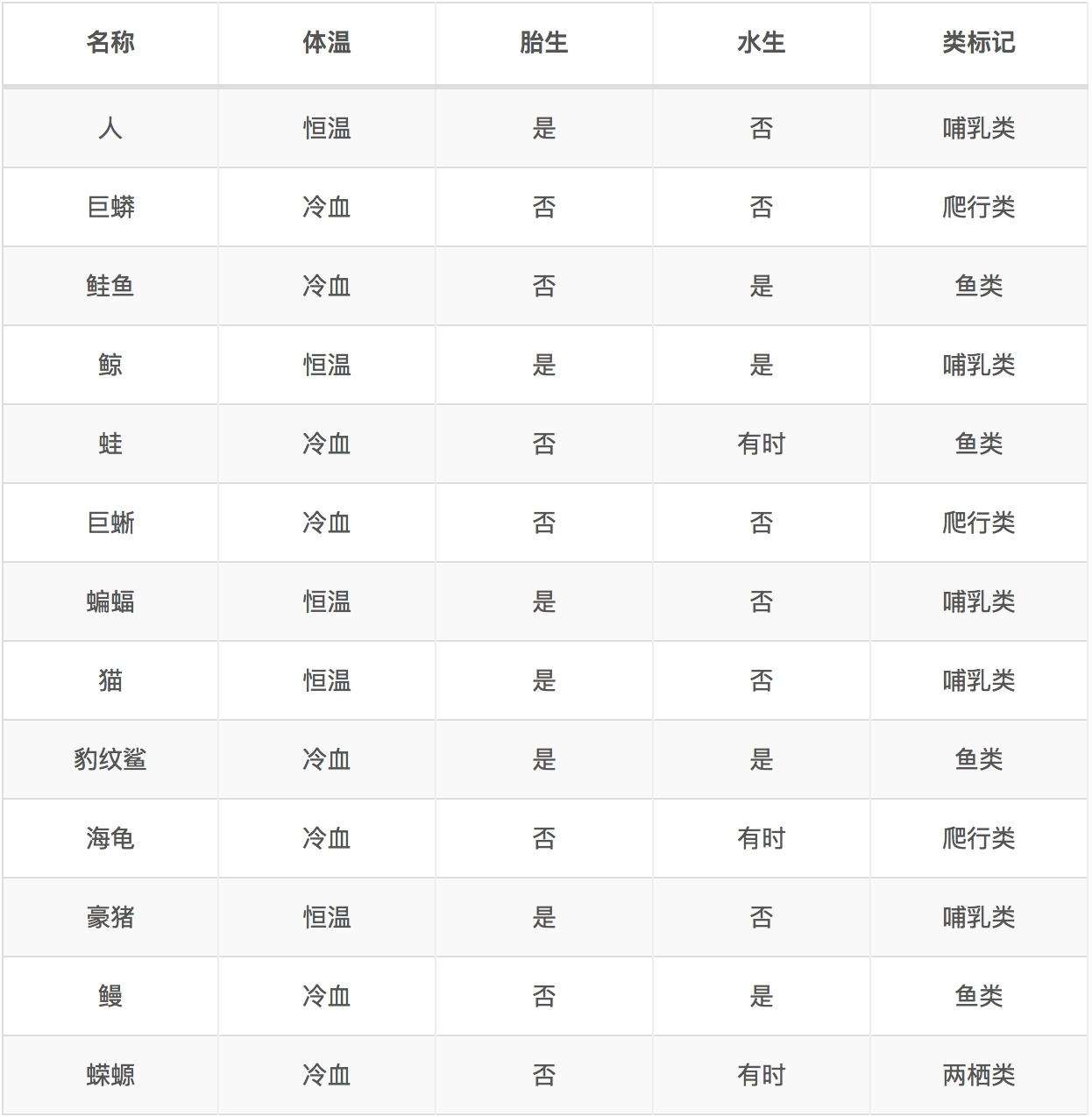
针对上述离散型数据，按照体温为恒温和非恒温进行划分。其中恒温时包括哺乳类5个、鸟类2个，非恒温时包括爬行类3个、鱼类3个、两栖类2个，如下所示我们计算D1,D2的基尼指数。


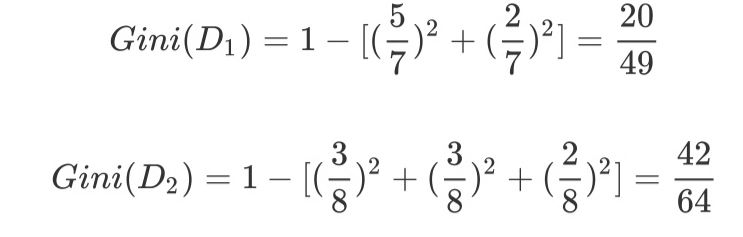
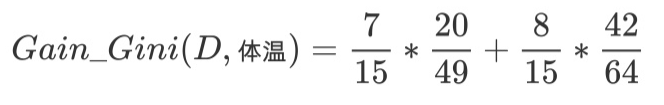
然后对每个特征都计基尼系数， 最后选择基尼系数最小的特征和相应的划分
PS。 如果特征多有离散的特征值如(young, middle, old) 会有如下划分
{(‘young’), (‘middle’, ‘old’)}
{(‘middle’), (‘young’, ‘old’)}
{(‘old’), (‘middle’, ‘young’)}
如果有4个离散值，就有7种划分可能。
如果有5个离散值，就有15种划分可能。
所以，如果特征里面离散值过多的话，是不太适合用CART的

对于连续性特征问题，其实有限数据，也可以视为多特征的离散值。
将数据排序，然后根据指定点切分。 总共有N-1种切分。 然后算基尼系数最小的就可以了

回归树原理

区别于分类树，回归树的待预测结果为连续型数据。同时，区别于分类树选取Gain_GINI为评价分裂属性的指标，回归树选取Gain_σ为评价分裂属性的指标。选择具有最小Gain_σ属性及其属性值，作为最优分裂属性以及最优分裂属性值。Gain_σ值越小，说明二分之后的子样本的“差异性”越小，说明选择该属性（值）作为分裂属性（值）的效果越好。

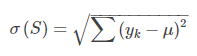
其中，μ表示样本集S中预测结果的均值，yk表示第k个样本。 可以这么理解。把数据分在一个箱子里面，然后用箱子的均值就是预测值。这个就是方差了。 回归树就是争取做到方差最小（就是与实际值越接近）

试着想一下，如果总共有100条数据，分了100个箱子， 那均值 = 自身。 方差为0

决策树防止过拟合手段

上面说的100条数据，分100个箱子，也就是过拟合状态了。 理论上一直分一直分， 可以得到方差为0的决策树。

避免这个问题就要对树进行剪枝了。
由于时间关系，请各位大侠参考这篇文章
https://blog.csdn.net/zhengzhenxian/article/details/79083643

模型评估

混淆矩阵
AOC
ROC

sklearn参数详解，Python绘制决策树

参数含义：

1. criterion:string, optional (default=“gini”)

   (1).criterion='gini',分裂节点时评价准则是Gini指数。
   (2).criterion='entropy',分裂节点时的评价指标是信息增益。
   

2. max_depth:int or None, optional (default=None)。指定树的最大深度。

   如果为None，表示树的深度不限。直到所有的叶子节点都是纯净的，即叶子节点
   中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。
   

3. splitter:string, optional (default=“best”)。指定分裂节点时的策略。

   (1).splitter='best',表示选择最优的分裂策略。
   (2).splitter='random',表示选择最好的随机切分策略。
   

4. min_samples_split:int, float, optional
   (default=2)。表示分裂一个内部节点需要的做少样本数。

   (1).如果为整数，则min_samples_split就是最少样本数。
   (2).如果为浮点数(0到1之间)，则每次分裂最少样本数为ceil(min_samples_split * n_samples)
   

5. min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。

   (1).如果为整数，则min_samples_split就是最少样本数。
   (2).如果为浮点数(0到1之间)，则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)
   

6. min_weight_fraction_leaf:float, optional (default=0.)

   指定叶子节点中样本的最小权重。
   

7. max_features:int, float, string or None, optional (default=None).

   搜寻最佳划分的时候考虑的特征数量。
   (1).如果为整数，每次分裂只考虑max_features个特征。
   (2).如果为浮点数(0到1之间)，每次切分只考虑int(max_features * n_features)个特征。
   (3).如果为'auto'或者'sqrt',则每次切分只考虑sqrt(n_features)个特征
   (4).如果为'log2',则每次切分只考虑log2(n_features)个特征。
   (5).如果为None,则每次切分考虑n_features个特征。
   (6).如果已经考虑了max_features个特征，但还是没有找到一个有效的切分，那么还会继续寻找
   下一个特征，直到找到一个有效的切分为止。
   

8. random_state:int, RandomState instance or None, optional
   (default=None)

   (1).如果为整数，则它指定了随机数生成器的种子。
   (2).如果为RandomState实例，则指定了随机数生成器。
   (3).如果为None，则使用默认的随机数生成器。
   

9. max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。

   (1).如果为None,叶子节点数量不限。
   (2).如果为整数，则max_depth被忽略。
   

10. min_impurity_decrease:float, optional (default=0.)

    如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。
    加权不纯度的减少量计算公式为：
    min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
    - N_t_L / N_t * left_impurity)
    其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数，
    N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指
    分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。

11. min_impurity_split:float

    树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。
    这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。

12. class_weight:dict, list of dicts, “balanced” or None, default=None

    类别权重的形式为{class_label: weight}
    (1).如果没有给出每个类别的权重，则每个类别的权重都为1。
    (2).如果class_weight=‘balanced’，则分类的权重与样本中每个类别出现的频率成反比。
    计算公式为：n_samples / (n_classes * np.bincount(y))
    (3).如果sample_weight提供了样本权重(由fit方法提供)，则这些权重都会乘以sample_weight。

13. presort:bool, optional (default=False)

指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时，对于大数据集
会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。

最后

以上就是魁梧路灯为你收集整理的决策树信息论基础（熵 联合熵 条件熵 信息增益 基尼不纯度）决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景回归树原理决策树防止过拟合手段模型评估sklearn参数详解，Python绘制决策树的全部内容，希望文章能够帮你解决决策树信息论基础（熵 联合熵 条件熵 信息增益 基尼不纯度）决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景回归树原理决策树防止过拟合手段模型评估sklearn参数详解，Python绘制决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。