数据对象和属性类型

中心性度量 – 众数

• 众数（mode）是另一个衡量中心性的测量。众数是一 系列数据中出现频率高的值。
• 众数可以是定性的也可以是定量的属性。有可能好几 个不同的值都出现大量的频率，导致众数不止一个 众数有1个、2个、3个的分别称为unimodal（单峰值）, bimodal（二峰值）, trimodal（三峰值）
• 一个极端的例子，如果每个数据值都仅出现一次，则 没有众

中心性度量 – 中列数

• 中列数(midrange)是数据集中大值和小值的平均值。 可以用来评估数值型数据的中心性趋势。 举例： 假设我们有salary的如下值（以千美元为单位），按递 增次序显示：30,31,47,50,52,52,56,60,63,70,70,110 求其中中列数 中列数是：30+110/2=70

数据的对称和偏斜

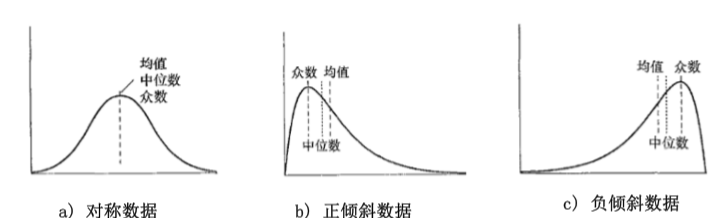
• 在对称的单峰频率曲线数据分布中，平均数，中值和众数 都在同样的中点值上。
• 实际应用中，绝大部分都不是对称的。如果众数的值小于 中值，称为正偏斜；如果众数的值大于中值，称为负偏斜

数据的基本统计描述

数据分散性度量：方差和和标准差

方差和和标准差

方差和标准差是测量数据分散度的

标准差的基本属性

• 标准差测量的是数据偏离均值的发散程度，因此只有在均值 接近数据中心的时候才考虑。
• 标准差为0只有在所有数据值都相等时才发生

数据分散性度量：极差

• 令x1, x2, … xN是某个数值属性X的一系列观察，数据 集的极差表示的是大值和小值的差

数据分散性度量 偏度（Skewness）

• 是统计数据分布偏斜方向和程度的度量

数据分散性度量 峰度（Kurtosis）

• 描述总体中所有取值分布形态陡缓程度的统计量

数据分散性度量：分位数

1. 假设数据按照属性X升序排列。我们可以挑选特定的数 据点把数据分割成大小相等的连续数据集
2. 分位数是数据分布上有一定间隔的数据点，将数 据分成基本相等大小的连续数据集。
   – 2‐分位点把数据划分为高低两半。即中位数。
   – 4‐分位点（quartile）是把数据分布分成4个等量大小的3 个数据点，每一个部分表示数据分布的1/4. 它们被称为 四分位数。
   –100‐分位数（percentile，百分位数）将数据集分成100 个大小相等的连续集合。
3. 给定第k个q‐分位点x, 至多k/q的数据值小于x，至多q‐k/q 的数据值大于x。k是大于0小于q的整数。共有q‐1个q分位点。
4. 分位数反应了分布的中心，散布以及形状。
5. 第1个四分位数，表示为Q1, 是第25个百分位点。它把数 据值低的25%切断。第3个四分位数，表示为Q3，是第 75个百分位数。它切断了数据值低的75%。
6. Q1和Q3的距离，简单反应了数据中心的一半数据的范围。 这个距离被称为四分位数极差(IQR)。被定义为：
   IQR = Q₃ - Q₁

数据分散性度量：五数概括

单个的数值分散性测量在描述偏斜分布时不够有效。 在对称的分布中，中值把数据分成大小相等的2部分。 但对偏斜的数据来说并非如此
五数概括（Five‐number summary）由中值，Q1，Q3， 小值和大值组成，按次序表示为：Minimum, Q1, Median, Q3, Maximum.

数据可视化

数据分散性度量：盒图

• 盒图体现了五数概括。
• 盒子的端点在四分位数上， 盒的长度是四分位数极差 (IQR)
• 中位数是箱子中间的线
• 盒子外面的两根须是观察 的大值和小值
• 箱线图的计算时间复杂度 是o(nlogn).

衡量数据相似性和相异性

数据矩阵

相异性矩阵

相异性矩阵，存放n个对象两两之间的邻近度，d(i,j) 越 接近值越趋近于0，越不同值越大

那么我们也可以由相异性度量推出相似性。例如，对于标称属性来说。

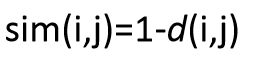
总结

最后

以上就是漂亮冰棍为你收集整理的商务智能与数据挖掘 - 认识数据数据对象和属性类型数据的基本统计描述数据可视化衡量数据相似性和相异性总结的全部内容，希望文章能够帮你解决商务智能与数据挖掘 - 认识数据数据对象和属性类型数据的基本统计描述数据可视化衡量数据相似性和相异性总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。