问题

在优化问题中，有一种常见的问题：已知样本集合，求拟合直线。拟合直线的一个选取原则是使样本点到拟合直线的距离最短。这里就是研究在$n$维样本点$[x_1,x_2,...,x_n]$到$n$维直线的距离。我采用向量研究这个问题，向量在多维情形下易于理解。

解答

二维向量

先考虑二维向量的情形，即二维平面的的点$A(x_0,y_0)$到直线$l:0=w_{1}x+w_{2}y+b$的距离.原点$O(0,0)$,所以向量$OA=(x_0,y_0)$,如果把OA沿直线$l$作正交分解，即分解为垂直于直线与平行直线两部分，那么$OA=e+p$,其中$e$垂直于$l$，$p$平行于$l$.$e$的长度就是点到直线的距离。
现在假设直线l的一个法向量为z，那么ez平行，所以
$OA\ast z=(e+p)z=ez+pz=ez+0=ez=|z||e|$
这说明求得一个法向量$z$，就可以得到点到直线的距离了。

n维向量

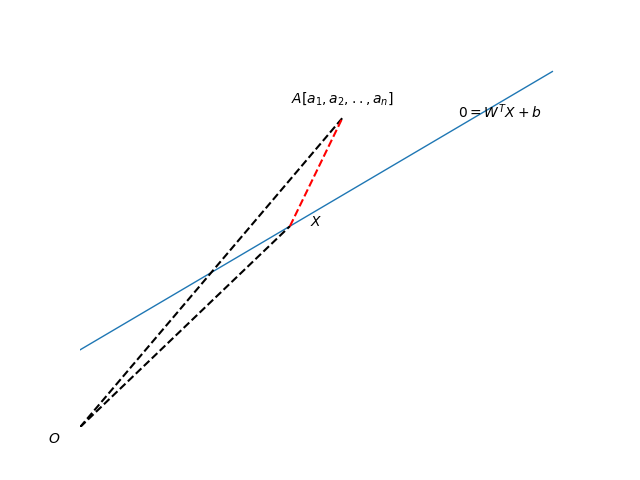
如下图所示，设有:
点$A:[a_1,a_2,...,a_n{]}^T=a$,
直线方程:$W^{T}X+b=0,W^T=[w_1,w_2,...,w_n]$
向量$OA=[a_1,a_2,...,a_n{]}^T$
向量$OX=[x_1,x_2,...,x_n]=x$
则向量$XA=a-x$
由于$0=W^T(X+\frac{W}{||W|{|}^2}b)$，所以直线的一个法向量为:$W^T$
向量XA在直线的法向量$W^T$上的投影即为A到直线的距离。
XA可分解为平行($p$)和垂直($e$)于直线的两部分:$XA=a-x=p+e$
计算两个向量的点积:
$W^T\ast XA=W^{T}p+W^{T}e=W^{T}e=||W||||e||$
$W^T\ast XA=W^T(a-x)=W^{T}a-W^{T}x=W^{T}a+b$

所以点到直线的距离为:
$$\frac{|W^T+b|}{||W||}$$

最后

以上就是饱满萝莉为你收集整理的n维点到直线的距离问题解答的全部内容，希望文章能够帮你解决n维点到直线的距离问题解答所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。