文章目录
- 一、softmax
- 二、损失函数loss
- 1、均值平方差
- 2、交叉熵
- 3、损失函数的选取
- 三、softmax 算法与损失函数的综合应用
- 1 验证softmax_cross_entropy_with_logits包含softmax函数
- 2 验证非标准one_hot的交叉熵 结果对于错误分类不明显
- 3 验证labels = [2 , 1] 即 001 与 010
- 4 验证loss = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
- 5 验证loss_2 = -tf.reduce_sum(labels * tf.log(tf.nn.softmax(logits)))
- 四、总结:
一、softmax
常见的激活函数输出值只有两种,现实中需要多种分类,需要判断输入属于分类的概率,
这样就引入了分类函数softmax函数,
softmax = exp( logits)/reduce_sum( exp( logits), dim)
softmax网络模型
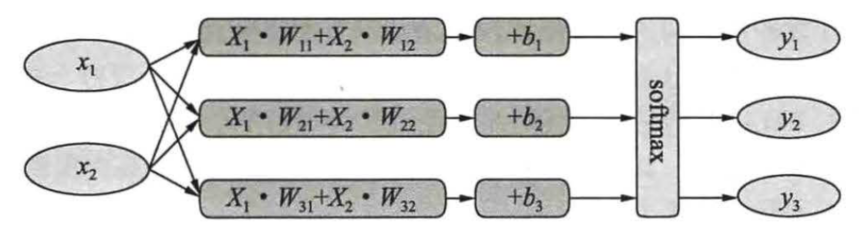
二、损失函数loss
用真实值与预测值的距离来指导模型的收敛万向
1、均值平方差
- tf方法
1
2
3
4
5
6MSE=tf.reduce_mean (tf.pow(tf.sub(logits, outputs) ,2.0)) MSE=tf.reduce_mean (tf.square(tf.sub(logits, outputs))) MSE=tf.reduce_mean (tf.square(logits-outputs)) Rmse= tf.sqrt(tf.reduce_mean(tf.pow (tf. sub(logits, outputs) , 2.0 ) )) mad= tf.reduce_mean (tf.complex_abs(tf.sub(logits, outputs))
2、交叉熵
一般用在分类问题上，表达的意识为预测输入样本属于某一类 的概率。
其表达式见式 (6-1 3) ，其中 y 代表真实值分类 ( 0 或 1) , a代表预测值。
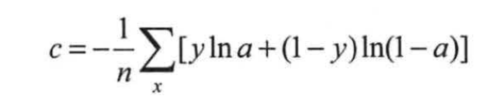
- tf方法
3、损失函数的选取
损失函数的选取取决于输入标签数据的类型:
如果输入的是实数、无界的值，损失函数使用平方差:
如果输入标签是位矢量〈 分类标志) ，使用 交叉;脑会更适合。
三、softmax 算法与损失函数的综合应用
1 验证softmax_cross_entropy_with_logits包含softmax函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30# 交叉熵 # 两次sotfmax实验,将输出值logits分别进行两次softmax,观察两次区别意义 # 将上面的两个值进行softmax_cross_entropy_with_logits import tensorflow as tf labels = [[0,0,1],[0,1,0]] # 标签labels logits = [[2,0.5,6], [0.1, 0, 3]] # 一个网络输出logits logits_scaled = tf.nn.softmax(logits) # 激活函数,输出为总输出的概率, 总和为1, logits_scaled_2 = tf.nn.softmax(logits_scaled) # 经过二次softmax后, 分布概率会有所变化, 所以说第一次logits_scaled才是正经的结果 result1 = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits) # 传入的logits是不需要进行softmax, result2 = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits_scaled) # 如果将softmax后的值传入,就相当于进行了两次softmax,论证标题 result3 = -tf.reduce_sum(labels*tf.log(logits_scaled),1) # 防止二次使用softmax处理数据, 自写交叉熵 with tf.Session() as sess: print("损失函数值 logits_scaled=",sess.run(logits_scaled),/ sum(list(sess.run(logits_scaled))[0]),"n") print("损失函数值 logits_scaled_2=", sess.run(logits_scaled_2),"n") print("交叉熵 result1=",sess.run(result1),"n") print("交叉熵 result2=",sess.run(result2),"n") print("交叉熵 result3=",sess.run(result3),"n")
1
2
3
4
5
6
7
8
9
10
11
12损失函数值 logits_scaled= [[0.01791432 0.00399722 0.97808844] [0.04980332 0.04506391 0.90513283]] 0.9999999781139195 损失函数值 logits_scaled_2= [[0.21747023 0.21446465 0.56806517] [0.2300214 0.22893383 0.5410447 ]] 交叉熵 result1= [0.02215516 3.0996735 ] 交叉熵 result2= [0.56551915 1.4743223 ] 交叉熵 result3= [0.02215518 3.0996735 ]
- 总结:
对于已经用softmax转化过的scaled,在计算loss时不能用tf里面的softmax_cross_entropy_with_logits函数,可以自己写 例如result3
2 验证非标准one_hot的交叉熵 结果对于错误分类不明显
1
2
3
4
5
6
7
8
9# 验证非标准one_hot交叉熵的结果对于错误分类不明显 labels = [[0.4,0.1,0.5],[0.3,0.6,0.1]] # 标签总概率为1, 非标准one hot logits = [[2,0.5,6], [0.1, 0, 3]] result4 = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits) with tf.Session()as sess: print("result4=", sess.run(result4)) # 比较前面的发现 ， 对于正确分类的交叉熵和错误分类的交叉熵 ， 二者的结果差别 # 没有标准 one-hot 那么明显。
1
2result4= [2.1721554 2.7696736]
3 验证labels = [2 , 1] 即 001 与 010
1
2
3
4
5
6
7#sparse 标签de 交叉熵使用, 与result1一样 labels = [2 , 1] # # labels[2 ， 1] 等价 one hot编码中的 001 与 010 logits = [[2,0.5,6], [0.1, 0, 3]] result5 = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits) with tf.Session()as sess: print("result5=", sess.run(result5))
1
2result5= [0.02215516 3.0996735 ]
4 验证loss = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
1
2
3
4loss = tf.reduce_sum(result1) # 这就是根据交叉熵最终得到的损失值 with tf.Session()as sess: print("loss=", sess.run(loss))
1
2loss= 3.1218286
5 验证loss_2 = -tf.reduce_sum(labels * tf.log(tf.nn.softmax(logits)))
1
2
3
4
5
6
7
8# 对于result3这种己经求得softmax的情况下求loss 可以把公式进一步简化成: # labels = [2,1] labels = [[0,0,1],[0,1,0]] logits = [[2,0.5,6], [0.1, 0, 3]] loss_2 = -tf.reduce_sum(labels * tf.log(logits_scaled)) with tf.Session()as sess: print("loss_2=", sess.run(loss_2))
1
2loss_2= 3.1218288
四、总结:
本节介绍如何通过输出值跟交叉熵求loss的方法
输出值–> softmax --> reduce_sum
logits_scaled = tf.nn.softmax(logits) --> loss_2 = -tf.reduce_sum(labels * tf.log(logits_scaled))
result1 = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits) --> loss = tf.reduce_sum(result1)
即输出求交叉熵有两种,
tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits)
-tf.reduce_sum(labels*tf.log(logits_scaled),1)
输出求损失loss有两种
loss = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
loss_2 = -tf.reduce_sum(labels * tf.log(tf.nn.softmax(logits)))
最后
以上就是长情流沙最近收集整理的关于7_交叉熵_softmax_损失函数loss_分析一、softmax二、损失函数loss三、softmax 算法与损失函数的综合应用四、总结:的全部内容，更多相关7_交叉熵_softmax_损失函数loss_分析一、softmax二、损失函数loss三、softmax内容请搜索靠谱客的其他文章。
发表评论 取消回复