002-深度学习数学基础(神经网络、梯度下降、损失函数)

这里在进入人工智能的讲解之前，你必须知道几个名词，其实也就是要简单了解一下人工智能的数学基础，不然就真的没办法往下讲了。

本节目录如下：

• 前言。
• 监督学习与无监督学习。
• 神经网络。
• 损失函数。
• 梯度下降。

0. 前言

人工智能可以归结于一句话：针对特定的任务，找出合适的数学表达式，然后一直优化表达式，直到这个表达式可以用来预测未来。

接下来就来一句一句的分析这句话：

• 针对特定的任务：

首先我们需要知道的是，人工智能其实就是为了让计算机看起来像人一样智能，为什么这么说呢？举一个人工智能的例子：

我们人看到一个动物的图片，就可以立刻知道这个动物是猫，还是狗。但是计算机却不可以，如果计算机可以分出类别，那么这就会是一个具有图像分类功能的人工智能小例子。

这里的图像分类就是我们所说的特定任务，这就是我们希望写出一个人工智能的程序来做的事情。

还有一些其他的常见的任务：人脸识别,目标检测,图像分割,自然语言处理 等等。

• 找出合适的数学表达式：

学过高等数学并且有计算机思维的人都知道，世界中几乎所有的事情都可以用数学函数来表达出来，我们先不管这个数学表达式是离散还是连续，也不管他的次数多高，反正他能达到表示特定任务的一种目的。

比如说，针对一个西瓜质量好坏的预测任务，可以设出以下的表达式：
$$f(x)=a\ast x_1+b\ast x_2^2+c\ast x_3^3+d$$
解释如下：

1、$$x1，x2，x3$$ 可以看作判断西瓜好坏的判断依据，比如可以是：瓜皮纹路，敲击声音，瓜皮颜色等等。

2、$$a，b，c，d$$ 就是这个表达式的系数，一旦数学表达式定下来了，那么接下来需要做的事情就是找出合适的系数，使得这个表达式可以很好的判断出西瓜质量的好坏。

所以，针对上文提到的特定任务，都可以用数学表达式表示出来，当然，我们会尽可能找简单、高效的表达式。

• 一直优化这个表达式：

上边引出表达式之后，会发现当表达式确定下来之后，就要寻找合适的系数了，寻找系数的过程就被称之为训练网络的过程。

我们优化表达式的重要思想是：一直调整系数值，使得预测出的数据 与 真实数据之间的差距尽可能的最小。

比如：假设预测的数据是 $$f_1(x)$$，真实数据是$$y$$，我们通过一直改变系数的值，来找出可以使得预测数据与真实数据之间距离最小的一组，最小的一组数据就是我们需要的系数。

其中，距离计算公式可以是如下的表达式：
$$loss=\sqrt{(f_1(x)-y{)}^2}$$
通过这个表达式，得到的 loss 值就是真实值与预测值之间的距离。

然后，接下来的优化就是针对这个loss 表达式来进行的，目的就是让loss的值达到最小。

因为loss值达到最小的时候，就意味着我们的预测值与真实值距离很相近，预测越准确。

这里值得一提的是，这里的loss表达式的优化过程，其实就是将loss公式对函数f(x)的系数求导。

所以当loss最小的时候，就意味着此时的系数最合适。

具体的细节往下看。

• 用优化好的表达式预测未来：

经过上边的优化，此时函数会得到一个相对好一点的系数，然后就可以使用这个函数来预测未来的事情了。

这就是达到了人工只能的目的了。

所以，下边我们就要仔细讨论，数学表达式的构建，距离函数的构建，距离的优化。

1. 神经网络

神经网络的英文是：neural network （简称：NN）。

神经网络其实就是变形的数学表达式，它通过拼装基础组件（神经元）来模拟出数学表达式。

1.01. 什么是神经网络

一说神经网络，大家首先想到的就是神经元，其实没错，神经网络这个名词就是从神经元这里演变过来的。所以我们做一下类比。

1.01.001. 神经元

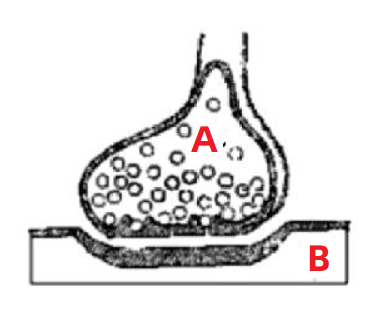
如图所示，这个图就是我们人体的神经元的放大图。

通常我们身体的 A 部位发出的命令，要指挥 B 部位响应，就要通过 A 向 B 发出信号。这个信号的强弱影响着 B 反应的强弱。

所以，这就是神经网络的构思所在：

构建出一个类似于神经元的结构，上一个节点的输入（A处的控制） 以及权重（信号的强弱）共同决定下一个节点的输出（B处的反应）。

这句话，现在看不懂没关系，有个印象就好，继续往下看吧。

1.01.002. 神经网络

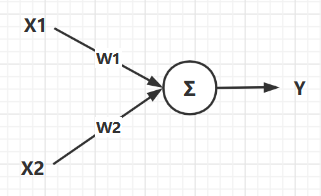
如图所示就是一个最简单的神经网络结构，这个结构的数学表达式是：$Y=X1\ast W1+X2\ast W2$ 。

图中的圆圈我们就把他类比于神经元，图中的各个结构解释如下：

• 其中 X1,X2 就是这个神经网络的输入，他相当于就是人体大脑发出的控制命令。

• W1,W2 就是权重，他是用来控制不同输入信号占比大小的数据，比如：想让控制X1作用明显一点，那么对应的W1就大一点。

• Y 就是输出，他就是输入数据与权重作用之后的最终结果，在神经元中也就是最终对身体某个部位的控制信号。

1.02. 神经网络的数学原理

神经网络的数学原理非常简单，简单总结下来就是一句话：不同的输入作用于各自的权重之后的和即为我们需要的结果。

其实就可以大致理解为我们的函数 ： $$f(x)=a\ast x1+b\ast x2$$ 一样，所谓的权重就是我们方程的系数。

细心的人观察上边的公式就会发现，一个神经元节点就可以归结于一个运算式子。所以我们这里就来针对上图，分析分析含有一个神经元节点的公式。

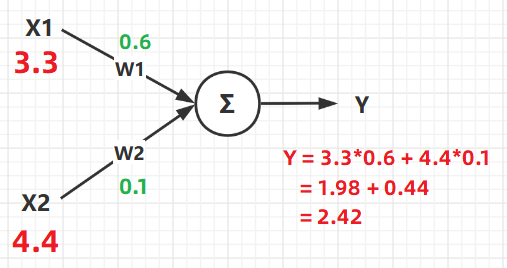
从图中可以看得出来，最终的输出结果 Y 是由 输入（X） 以及 权重（W） 共同决定的。

他们最终的计算结果 Y 其实说白了就是一个计算公式：$Y=X1\ast W1+X2\ast W2$ ，这个公式的含义大家应该都明白，给不同的输入 分配不同的权重 ，从而得到想要的结果。

这就是神经网络中一个神经元的数学原理，当把神经元的个数增多之后，原理以此类推，只不过是要增加权重W以及输入X的个数而已。

下边就可以看作是一个，含有两层的神经网络结构。

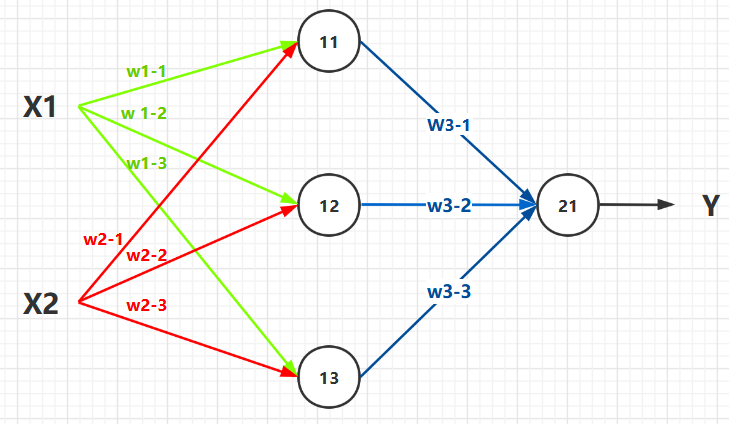
• 第一层节点： 11，12，13 。第二层节点： 21 。

• 输入： X1 ，X2 。 输出 ： Y 。

于是，根据公式：输出 等于 输入作用于 权重， 得出以下推导 ：

• 输入： X1 ，X2 。

• 节点11的值： $$Y_{11}=X_1\ast W_{1-1}+X_2\ast W_{2-1}$$ .

• 节点12的值： $$Y_{12}=X_1\ast W_{1-2}+X_2\ast W_{2-2}$$ .

• 节点13的值： $$Y_{13}=X_1\ast W_{1-3}+X_2\ast W_{2-3}$$ .

• 节点21的值就是最终输出 Y ： $$Y=Y_{21}=Y_{11}\ast W_{3-1}+Y_{12}\ast W_{3-2}+Y_{13}\ast W_{3-3}$$ .

所以，最终的整合式子为：
$$\begin{gathered} Y=Y_{11}\ast W_{3-1}+Y_{12}\ast W_{3-2}+Y_{13}\ast W_{3-3} \\ =(X_1\ast W_{1-1}+X_2\ast W_{2-1})\ast W_{3-1} \\ +(X_1\ast W_{1-2}+X_2\ast W_{2-2})\ast W_{3-2} \\ +(X_1\ast W_{1-3}+X_2\ast W_{2-3})\ast W_{3-3} \end{gathered}$$

于是，我们可以发现，类似于这样的堆叠方式，我们可以组合成很多的数学函数。

这就是神经网络，他的目的在于将数学公式堆砌出来，至于为什么要这样堆砌，是因为这样堆砌计算机计算比较方便呗。

1.03 总结

到目前为止你已经知道了神经网络的由来，并且知道神经网络与数学公式之间的关系。

此时你需要明确的知识点是：

• 人工智能就是使用已有的数据，拟合出一个可以用来预测未来的公式。
• 这个公式的系数需要一直调整，从而找出一组最为合适，正确率较高的系数。
• 因为系数的寻找需要大量的计算，所以需要将这个公式用神经网络表示出来的，因为在计算机中这样表示的时候计算最为方便。

2. 监督学习与无监督学习

这个知识点比较简单，就一些单纯的概念。

监督学习：就是我们收集到的数据是有标签的。

就是说，我们收集到的数据是已经分好类的。

比如说：当前当前有一批样本数据，

• x1, x2, x6, x9, x13属于类别y1类。
• x3, x4, x5, x8, x11属于类别y2类。
• x7, x10, x12属于类别y3类。

然后接下来我们使用这些数据的时候，就可以使用已有标签的数据，去拟合出曲线，用以预测未来。

无监督学习：我们收集到的数据是无标签的。

就是说，收集到的数据并没有固定的类别，我们需要做的事情就是挖掘数据内部的联系，给他们聚类，找出类别。

如图所示，挖掘出数据内部的联系，让他自动归类。

3. 损失函数

上边解释过了，损失函数的作用就是计算 真实值 与 预测值 之间距离的 （距离其实可以简单理解为两个数据之间的差距）。

这里介绍一些常见的几种损失函数，以供大家入门使用。

3.01. 一些前提

这里给定一些大前提，下边的几种损失函数通用的那种。

• 真实值：y ，他就是针对某一组输入x的真实标签。
• 预测值：f(x)，他就是针对输入x的预测标签。
• 样本数：m，他就是我们每次输入多少样本进行计算，比如：某一次输入5组x，得到5个预测结果，这里的m=5.

3.02. 绝对值损失函数

其实就是简单的计算 真实值 与 预测值 之间的绝对值距离而已。

公式：
$$J(y,f(x))=J(w,b)=\frac{1}{m}\sum _{i=1}^m|y_i-f(x_i)|$$
解释：

• $$J(y,f(x))$$ 的意思就是，这个损失函数的参数是：真是标签y 与 预测数据f(x) 。
• $$J(w,b)$$ 的意思是，这个损失函数的目的是优化参数 w 与 b 。这里的w，b其实就是系数的矩阵形式。
• 后边具体的计算公式就是：输入有m个样本，计算出这m个样本的距离绝对值和，然后再求均值。

3.03 均方差损失函数

就是将上边式子的绝对值换成平方就好了。

公式：
$$J(y,f(x))=J(w,b)=\frac{1}{2m}\sum _{i=1}^m(y_i-f(x_i){)}^2$$

解释：

• 这里只是将绝对值换成了平方，除以m换成了除以2m。

3.04 交叉熵损失函数

这个就比较麻烦了，交叉熵损失函数一般用于解决分类问题。

标签：

在通常的分类问题中，标签y的取值一般只有 0 或 1 。

1 表示是当前类别， 0 表示不是当前类别。

公式：
$$J(y,f(x))=J(w,b)=-\frac{1}{m}\sum _{i=1}^m(f(x)\ast log(y)+(1-f(x))\ast log(1-y))$$

解释：

• 上边说了，y 与 f(x) 都只能取 1 与 0 中的一种可能性。所以，上述公式的效果就是：
• 如果 y与 f(x) 相同，则 J = 0.

你带入 y=1 , f(x)=1 试试就知道了。

• 如果 y与 f(x) 不同，则 J = 无穷大.

你带入 y=1 , f(x)=0 试试就知道了。

3.05 总结

到这里你已经学习了三种常见的损失函数。

此时你应该有一个明确的知识点就是：

• 损失函数是用来计算真实值与预测值之间距离的。
• 当损失函数的值越小就代表着真实值与预测值之间的距离就越小，也就意味着预测的越准。

4. 梯度下降

好了好了，上边过完理论知识，这里来一个真真正正的数学内容了，其实不难，看我慢慢分析。

• 上边我们提到对数学函数优化的时候，只是介绍了理论的知识。

我们知道了损失函数就是衡量预测值与真实值之间距离的公式。

并且知道，损失函数的值越小，真实值和预测值之间的距离越小，也即：预测的越准。

• 但是并没有带着大家深入探究如何优化。

也就是没有告诉大家怎么使得损失函数的值越来越小。

其实，这里使用的数学知识就是 ：求偏导

4.01. 数学例子

这里以一个简单的数学例子来引入梯度下降的内容。

• 场景引入

在数学课中我们经常做的一个题型就是：已知一个函数f(x)的表达式，如何求出这个式子的最小值点。

在数学题中我们经常用的方法就是：将函数f(x)对x求导，然后令导数式子为0，求出此时的x的值，即为最小值点的位置。

• 具体例子

求函数 $$f(x)=2\ast x^2-12\ast x+20$$ 的最小值点，并且求出最小值。

对函数求导
$$f(x{)}^{\prime }=4\ast x-12$$
令导函数为0，求出此时的x
$$\begin{gathered} 令f(x{)}^{\prime }=0 \\ 即4\ast x-12=0 \\ 得到x=3 \end{gathered}$$
此时，x = 3 即为函数 f(x) 的最小值点，带入原方程 f(3)= 2*9-12*3+20 = 2.

这个解题过程，想必大家都很熟悉吧。

下边就分析一下这个过程的数学原理了

4.02. 数学例子原理

梯度就是导数。

针对上边提到的方程的最小值求解，其实就是求出其梯度（导数）为0的位置，就是其最低点的位置。具体看下图：

• 方程 $$f(x)=2\ast x^2-12\ast x+20$$ 图像如下：

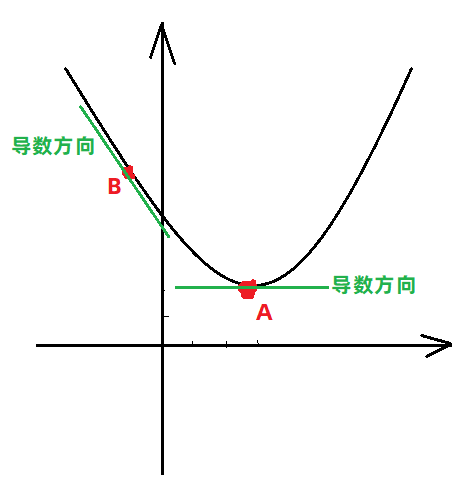
从图中可以看出，方程在不同位置的导数方向是不同的，只有在最低点的位置，导数为0，所以可以用导数为0的位置求出最低点。

上边举的例子是一个比较简单的例子，方程中只有一个未知数，但是在真实情况中，往往一个方程有很多未知数。

• 比如：$$f(x,y)=2\ast x^2+2\ast y+4\ast x\ast y$$

此时需要做的事情就是针对每一个变量求偏导，求出该方程针对每个变量的梯度方向 （梯度方向就是数据变小的方向）。

于是，在方程的每个点上，都有多个梯度方向，最终将这多个方向合并，形成这个点的最终梯度方向 （数据变小的方向）

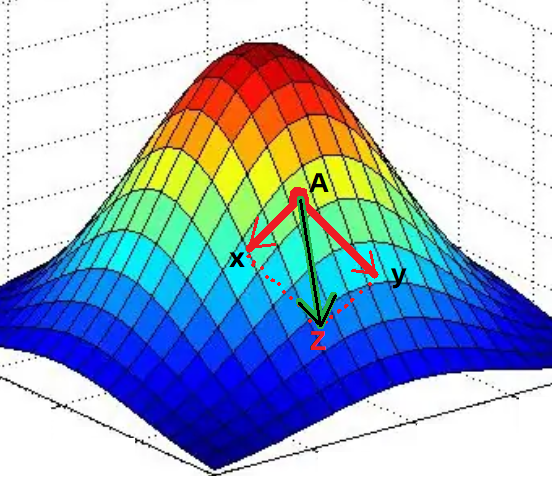
如图，方程有两个变量x,y，于是在A点针对两个变量求偏导就可以得到各自的梯度方向（两个红色箭头的方向）。

然后，将两个梯度进行合并，得到最终的梯度方向Z 。Z方向就是方程在A点数据变小的方向了。

4.03. 完整例子

上边讲完原理，这里就举出一个例子，带着大家走一遍梯度下降找最小值的过程。

假设此时的方程已知，并且根据方程绘制出的图像如下。

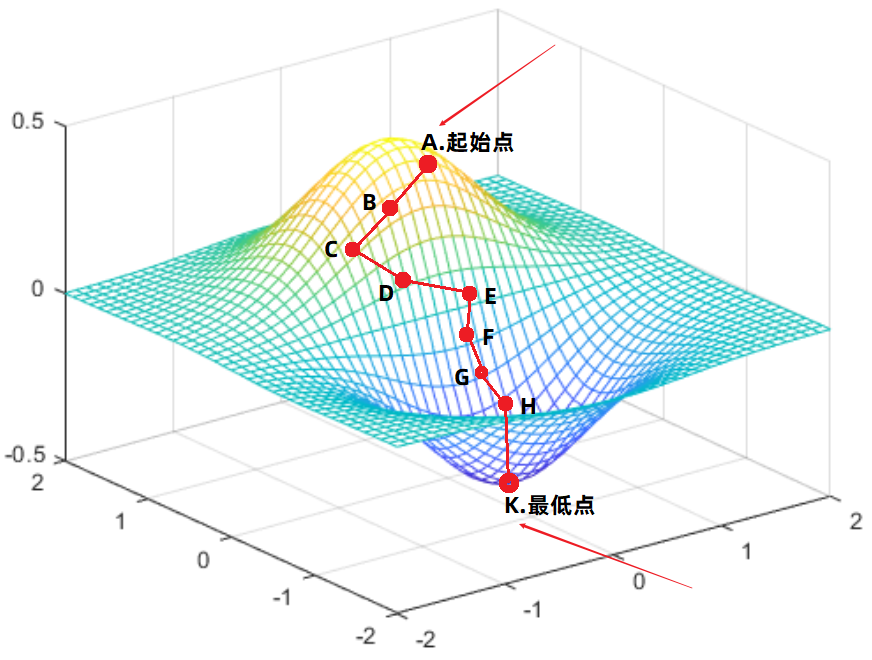
• 刚开始我们位于A点：

1、在A点处针对方程的各个变量求出偏导，于是便可以得到方程针对各个方向的梯度方向。

2、将A点处各个方向的梯度方向进行合并，形成最终的梯度方向。

3、最终的梯度方向就是AB方向。

4、于是向着AB方向走出一段距离，走到了B点。

• 到达B点： （思路同上）

1、求出B点处各个方向的梯度方向，然后合并所有梯度方向，得到最终的B点处梯度方向 BC。

2、于是沿着BC方向，走出一段距离，到达C点。

• …重复上述过程：

到达某个点之后，求出各方向的偏导数，然后合并得到最终的梯度方向。

然后沿着合并后的梯度方向走出一段距离到达下一个点。

然后在一直重复…

• 到达K点：

K点就是最终的点，这就是优化得到的最重点。

这就是整个找最小点的可视化过程，但是其中提到更新的数学细节并没有提到，所以下边提一下用到的数学更新公式吧

4.04. 更新公式

一般我们梯度下降更新的数据只有函数的系数，然后函数的系数可以分为两类：权重（W）+偏差（b）

所以，更新的时候也就针对这两个参数就好了。

变量定义：

• W ： 方程的权重。 （可以简单理解为方程变量前面的系数）
• b ：方程的偏差。 （可以简单理解为方程中的常数）

比如：$$f(x,y)=2\ast x^2+y^2+3$$ 中，2 , 1就是权重，3就是偏差。

公式：

• 更新权重W：$$W_{new}=W_{old}-\alpha \ast \frac{\partial L}{\partial w}$$.

原始点的权重是 $$W_{old}$$，原始点此时针对W的梯度方向是$$\frac{\partial L}{\partial w}$$.

$$\alpha$$ 就是一段距离长度（它就是我们上文一直提到的走一段距离）。

所以 $$\alpha \ast \frac{\partial L}{\partial w}$$ 表达的含义就是沿着 W的梯度走一段长度为$$\alpha$$ 的距离。

然后 新的W 就是 旧的W 减去那一段方向长度。

• 更新偏差：$$b_{new}=b_{old}-\alpha \ast \frac{\partial L}{\partial b}$$.

原理同 W .

这就是更新参数的整个梯度下降过程了。

5. 总结

到目前为止，基础的人工智能知识已经基本讲完了，这个时候我们再来仔细品味这句话。

针对特定的任务，找出合适的数学表达式，然后一直优化表达式，直到这个表达式可以用来预测未来。

或许你就会有不一样的体会了。

ok，下一节就讲一讲Pytorch的基础使用，然后就是最终的手写体数字识别任务了。

最后

以上就是迷人灯泡为你收集整理的002-深度学习数学基础(神经网络、梯度下降、损失函数)002-深度学习数学基础(神经网络、梯度下降、损失函数)的全部内容，希望文章能够帮你解决002-深度学习数学基础(神经网络、梯度下降、损失函数)002-深度学习数学基础(神经网络、梯度下降、损失函数)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。