0 写在前面
本文为了让初学者更加简单、直观地理解神经网络在训练中的技巧,以及明白为什么这样做能有效地提高训练效率,将神经网络中的本质过程一一阐述,弄清楚这些原理对初学者大有裨益。
本博客的内容绝大部分摘录于[日]斋藤康毅的《深度学习入门——基于Python的理论与实现》
1 输出层函数与损失函数的联系
神经网络在进行反向传播时,经过输出层函数得到预测输出与监督数据的差分 y i − t i y_i - t_i yi−ti,其中 y i y_i yi表示预测数据, t i t_i ti表示监督数据。神经网络的反向传播会把这个差分表示的误差传递给前面的层,这是神经网络学习中的重要性质。这样“漂亮”结果并不是偶然,实际上有如下的对应关系,使得反向传播能得到 y i − t i y_i - t_i yi−ti的结果。
| 输出层激活函数 | 损失函数 |
|---|---|
| Softmax | 交叉熵 |
| 恒等函数(y=x) | 平方和误差 |
还有其他激活函数与损失函数的对应关系都能通过数学解析或计算图推导得到。
2 参数的更新
- SGD:朝着当前所在位置的最大梯度前进,易陷入局部最优,梯度的方向可能并没有指向全局最优的方向。
- Momentum:引入超参数“阻力系数”,模拟小球在斜坡上滚动的物理过程。能克服SGD优化非均向(anisotropic)函数时低效。
- AdaGrad:学习率衰减的参数更新方法,Ada来源于Adaptive。希望随着学习的进行,学习率逐渐减小。AdaGrad会为参数的每个元素适当地调整学习率,参数中被大幅更新的元素的学习率会变小。
- Adam:融合了Momentum和AdaGrad的方法。除了学习速率又引入两个Momentum超参数。我认为参数的更新虽然得到了一定的优化,但是多引入了两个超参数,这使得人为因素的介入会极大地影响训练效果。
3 权重的初始值
权重的初始值必须多样化,避免设置为相同的值,这使得其拥有了对称性,导致在误差反向传播中所有的权重值都会进行相同的更新,从而使神经网络无法正常学习。为了防止“权重归一化”,必须随机生成初始值。
这里我们做一个简单的实验,观察权重初始值是如何影响隐藏层激活值的分布的。这个实验参考了Stanford的课程CS231n。
使用标准差为1的高斯分布初始化权重,激活函数使用Sigmoid,观察五层神经网络的隐层输出。
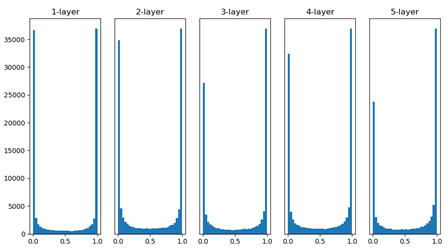
各层的激活值偏向0-1分布,随着输出不断靠近0或1,它的导数值之间接近0。因此,偏向0和1的数据分布会造成反向传播中梯度的值不断变小,最后消失。这个问题称为 “梯度消失”,深度学习中梯度消失的问题可能会更加严重。
将标准差设置为0.01,进行相同的实验,得到下图各层的激活值分布。
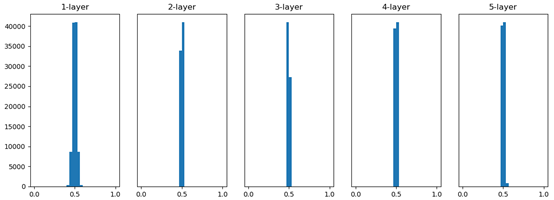
因为不像刚才的例子偏向0和1,所以不会发生梯度消失的问题,但是及果汁的分布有所偏向,说明在表现力上会有很大问题即“表现力受限”。因为如果有多个神经元都输出几乎相同的值,那么它们就没有存在的意义了,因为一个神经元就能表达基本相同的事情。
综上,如果传递的是有所偏向的数据,就会出现梯度消失或者“表现力受限”的问题,导致学习可能无法顺利进行。 激活函数使用Sigmoid或tanh等S型曲线函数时,使用“Xavier初始值”,激活函数使用ReLU时,使用“He初始值”。这样可以使得各层的激活值呈现出具有相同广度的分布。
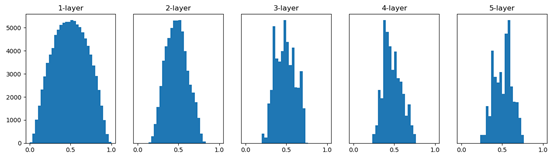
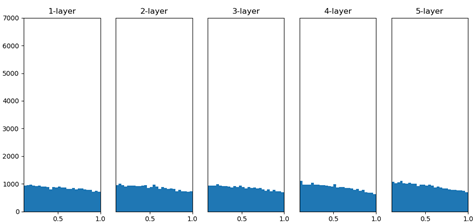
4 正则化
4.1 Batch Normlization
Batch Normalization(以下简称BN)的目的是为了使各层拥有适当地广度,而“强制性”地调整激活值的分布。 为此要在神经网络中插入对数据分布进行正规化的层,即BN层。具体来说就是学习时以mini-batch为单位进行数据均值为0、方差为1的正规化。
优点如下:
- 可以使学习快速进行
- 不那么依赖权重初始值
- 有效抑制过拟合(降低DropOut等的必要性)
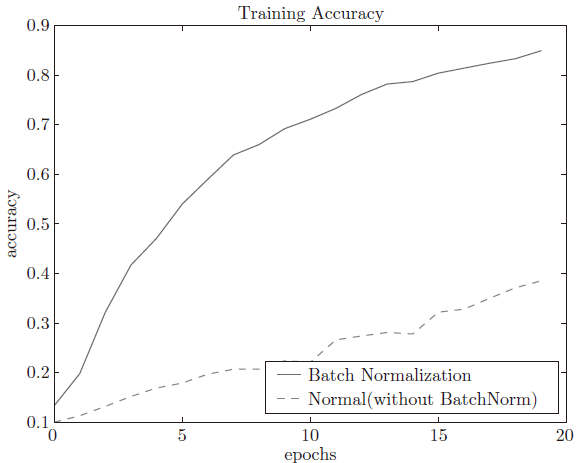
BN层插入到激活函数之前还是之后在文献[2-3]中已有讨论,我的理解是将此看作一个超参数,根据问题情况调整位置。
4.2 权值衰减
权值衰减也是一种防止过拟合的方法,通过为损失函数加上权重的L1、L2、L ∞ infty ∞范数,对学习过程中打的权重进行惩罚。其中L2范数最为常用,它会引入一个控制惩罚程度的超参数 λ lambda λ。
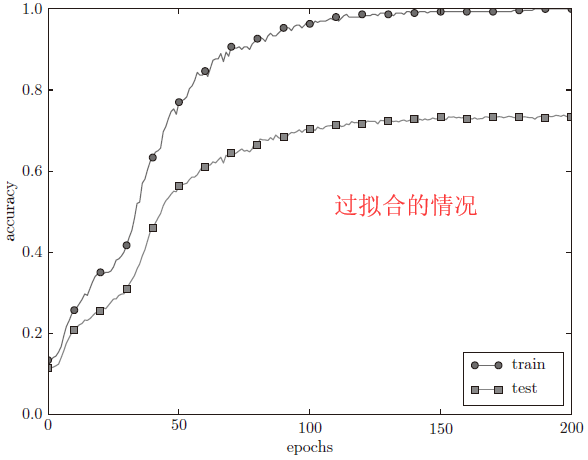
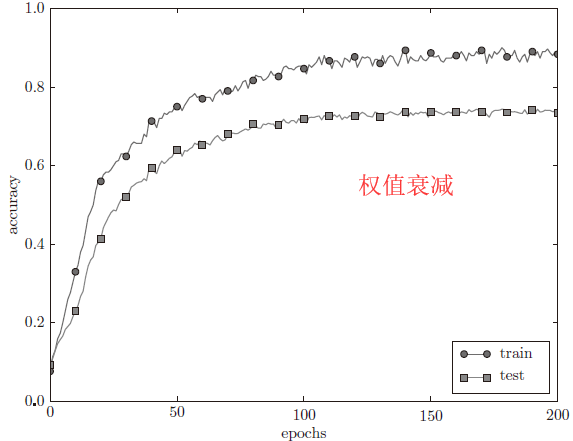
4.3 DropOut
在训练过程中随机删除神经元,被删除的神经元不能进行信号的传递,这样相当于是每次都训练了一个不同的模型,最终得到这些模型的一个综合输出,即它们的平均值,通常来说精度可以提高好几个百分点。需要注意的是正向传播时删除的神经元不能在反向传播时参与计算,即反向传播时信号无法通过删除的神经元。
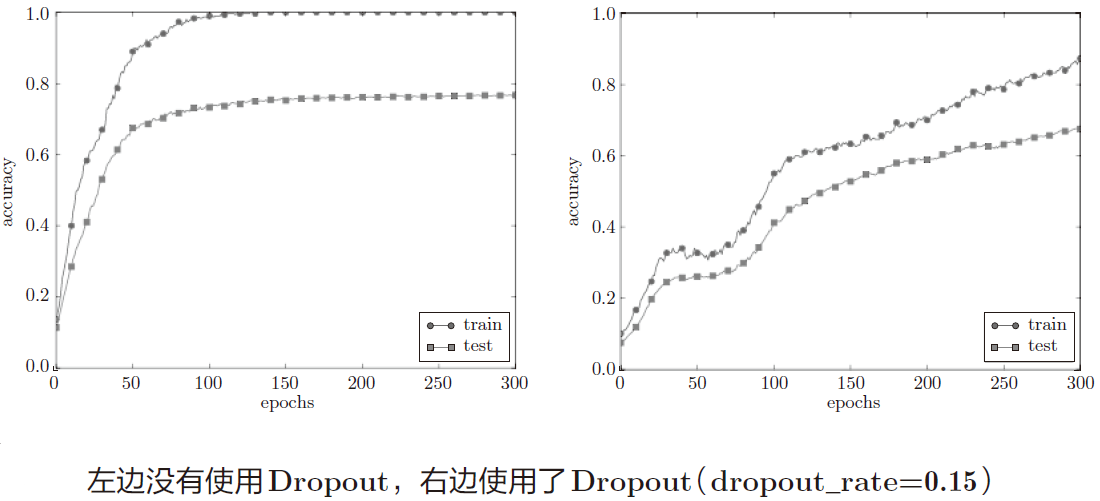
5 超参数
通俗来说就是包括所有需要人工设置的、具有强烈的主观的参数,如神经元数量、学习速率、batch大小等等。这类参数通常需要花费很大精力才能找到合适训练的,往往需要通过经验来设置,这也是为什么深度学习被称为“炼丹术”的主要原因。现将确定最优参数的步骤归纳如下:
- 设定超参数范围。给定一个大致的初始范围。
- 从设定的超参数范围中随机采样。
- 使用采样道得超参数值进行学习,通过验证数据评估识别精度。注意此步骤需要将eopch设置的很小,这样能极大缩短评估一次所需时间,节约计算资源。
- 重复步骤2和3(大约100次),根据它们的识别精度结果,缩小超参数的范围,最终能够得到较为满意的结果。
如果需要更精炼的方法,可以使用贝叶斯最优化(Bayesian optimization)。贝叶斯最优化运用以贝叶斯定理为中心的数学理论,能够更加严密、高效地进行最优化。详细内容请参考论文“Practical Bayesian Optimization of Machine Learning Algorithm”。
Reference
斋藤康毅. 《深度学习入门——基于python的理论与实现》[M]. 2016
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv:1502.03167, 2015.
Mishkin D, Matas J. All you need is a good init[J]. arXiv preprint arXiv:1511.06422, 2015.
最后
以上就是碧蓝寒风最近收集整理的关于神经网络的学习技巧(含损失函数与激活函数关系、初始值、优化函数、DropOut等等)0 写在前面1 输出层函数与损失函数的联系2 参数的更新3 权重的初始值4 正则化5 超参数Reference的全部内容,更多相关神经网络的学习技巧(含损失函数与激活函数关系、初始值、优化函数、DropOut等等)0内容请搜索靠谱客的其他文章。








发表评论 取消回复