|
在统计语言模型章节中,我们谈到了N元语法模型不可避免的一个问题,就是数据稀疏,其原因是大规模语料统计与有限语料的矛盾。根据齐普夫(Zipf)法则,我们能够推测知零概率问题不可避免。数据稀疏问题的解决办法就是进行平滑处理。平滑处理的算法有很多,本文将介绍众多算法中的佼佼者:古德-图灵(Good-Turing)平滑算法。 古德-图灵(Good-Turing)估计法是很多平滑技术的核心,于1953年有古德(I.J.Good)引用图灵(Turing)的方法而提出来的。其基本思想是:利用频率的类别信息来平滑频率。对于任何发生r次数的n元语法,都假设它发生了r*次。
其中,nr是训练语料中正好发生r次的N元组的个数。也就是说,发生r次的N元组的调整由发生r次的N元组与发生r+1次的N元组两个类别共同决定。统计数为r*次的N元组,其概率为:
我们注意到:
也就是说,N等于这个分布中最初的统计。那样,样本中所有事件的概率之和为
因此,可以这样说我们把你n1/N的概率剩量分配给未见事件。为了更好地理解古德-图灵(Good-Turing)估计法,以一个例子来讲解。 训练集合:T={<s>what is it what is small?}|T|=8 验证集合:V={what is it small ? <s> flying birds are a bird.}, |V|=12 在训练集合上,我们得到:p(<s>)=p(it)=p(small)=p(?)=0.125, p(what)=p(is)=0.25,其他为0 如果不经过平滑处理,则验证集上两句子的概率分别为:p(what is it?)=(0.25*2)*(0.125*2)≈0.001 p(it is flying.)=0.125*0.25*(0*2)=0 现在用古德-图灵算法进行平滑处理,如下: 首先计算,各发生r次N元组类别的数目,依次为N(0)=6,N(1)=4,N(2)=2,N(i)=0 ,i>2: 其次,重新估计各概率值。 对于发生0次的事件概率:Pr(.)=p(flying)=p(birds)=p(are)=p(bird)=p(a)=(0+1)*N(0+1)/(8*N(0))=1*4/(8*6)≈0.083 对于发生1次的时间概率:Pr(it)=p(<s>)=p(small)=p(?)=(1+1)*N(1+1)/(8*N(1))=2*2/(8*4)=0.125 对于发生两次的时间概率:Pr(what)=Pr(is)=(2+1)*N(2+1)/(8*N(2))=3*0/(8*2)=0: 保持原值0.25 归一化处理,6*P0+4*P1+2*P2=1.5。. 所以,归一化处理后,p’(it)=p’(<s>)=p’(small)=p’(?)= 0.125/1.5 ≈0.08, p’(what)=p’(is)= 0.25/1.5 ≈0.17, p’(.)=p’(birds)=p’(are)=p’(bird)=p’(a) = 0.083/1.5 ≈0.06 因此:p’(what is it?)=(0175*2)*(0.08*2)≈0.0002 p’(it is flying.) ≈ 0.08*0.17*(0.06*2)≈0.00004 |
最后
以上就是迷人灯泡最近收集整理的关于N元语法模型的数据稀疏问题解决方法之一:Good-Turing平滑的全部内容,更多相关N元语法模型内容请搜索靠谱客的其他文章。
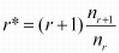
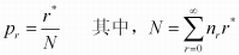
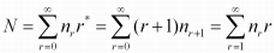
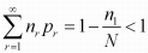








发表评论 取消回复