目的

我们讨论线性分类

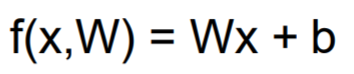
我们要做的：

1. 定义一个损失函数，来衡量我们对于训练出来的分数的不满意程度
2. 找到一个有效找到减少损失函数的参数的方式（优化）

多类支持向量机损失（Multiclass SVM Loss）

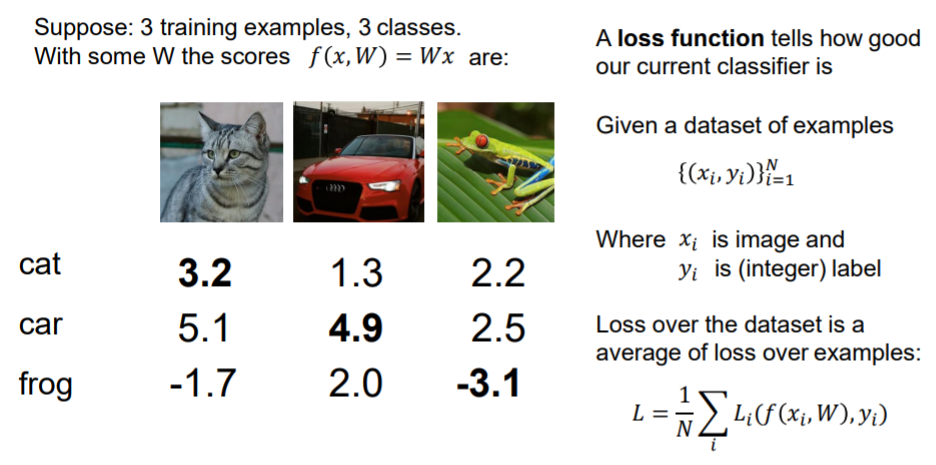
上图为例，3个样例，共3类，每个数据表示为（xi, yi），分别表示图片和对应标签

这个数据集的总体损失为每组损失 Li 的平均值

上图右下角意思为：若正确类别的分数比其他的分数都大于1，则表现完美，损失记为0，否则记为与这个差值+1。
所以可以简写为 0与Sj - Syi + 1 的最大值

举例：

三个相加后得该数据集总损失：

相应代码：

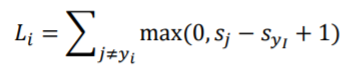
import numpy as np 

def L_i_vectorized(x, y, W):
	scores = W.dot(x)
	margins = np.maximum(0, scores - scores[y] + 1)
	margins[y] = 0
	loss_i = np.sum(margins)
	return loss_i

W与X乘得分数（即上图的一列3个数）
margins 即为执行上面 max函数所得结果，其中 y 项为0（自己与自己不可比较）
最后将margins 相加

问题

若发现一个W使L=0，这个W是随机的吗？
答：不是，2W也可使L=0
如：

正则（Regularization）

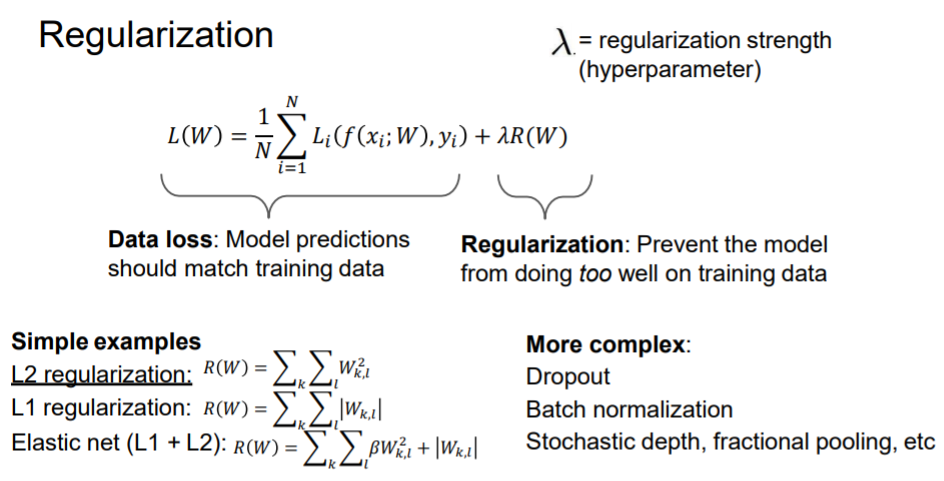
正则后的损失函数包含两部分：原损失，和防止模型在训练集上太好的正则项

Lanka为一个超参

通常使用的 L2正则， L1正则等

正则化优点

1. 权重偏好：L1 易产生稀疏解，L2 平滑稳定
2. 偏好简单模型
3. 通过添加曲率来改进优化
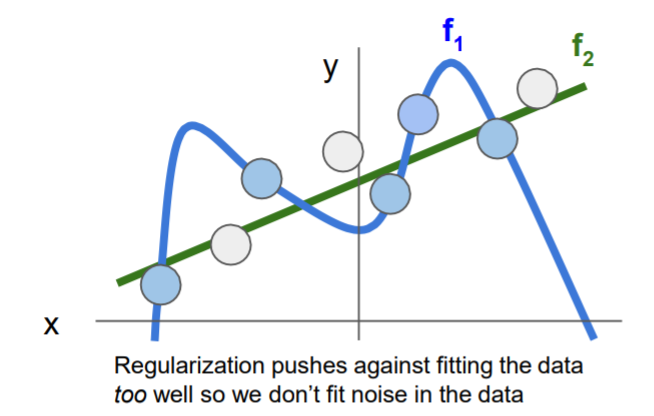
   正则化阻止数据过拟合，所以可以减少噪声影响

关于正则化，可参考： 正则化

Softmax分类器（Multinomial Logistic Regression）

我们希望将原始的分数用概率来解释

对于每一个预测图片的每一个分数，取其e^x，标准化得其概率，取其 -log 为Li，由log图像可知，概率越接近1，Li损失函数越小

简单来说，我们有了（X,Y）数据，有了分数函数，有了损失函数

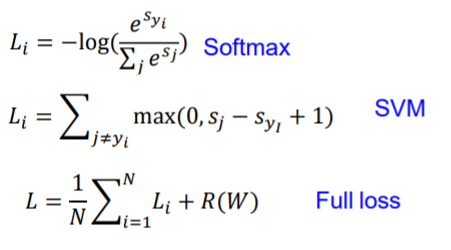
我们要得到最好的W

优化（Optimization）

策略一：随机寻找

精度很低

策略二：遵循斜率（梯度下降）

在一维中，函数的导数：

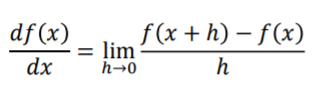
在多维度中，梯度是沿各维的(偏导数)向量。任何方向的斜率都是这个方向与梯度的点积。最陡下降的方向是负梯度

LOSS只是W的一个函数

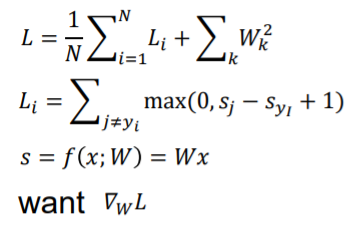
可以用微积分来计算

随机梯度下降（SGD）

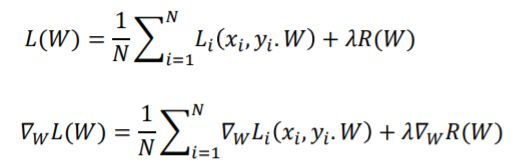
当N太大时，效率太低。我们使用minibatch来估算总体（通常选取32/64/128）

最后

以上就是认真饼干为你收集整理的神经网络与深度学习——损失函数与优化（CS231n）Loss Function and Optimization目的多类支持向量机损失（Multiclass SVM Loss）Softmax分类器（Multinomial Logistic Regression）优化（Optimization）的全部内容，希望文章能够帮你解决神经网络与深度学习——损失函数与优化（CS231n）Loss Function and Optimization目的多类支持向量机损失（Multiclass SVM Loss）Softmax分类器（Multinomial Logistic Regression）优化（Optimization）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。