空气中PM2.5问题的研究

50 阅读 0 评论 33 点赞

我是靠谱客的博主简单电源，最近开发中收集的这篇文章主要介绍空气中PM2.5问题的研究，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

最近在搞数模的东西，这算是一个对别人论文的方案的实现，自己再做一些拓展。

先上题目：PM2.5的相关因素分析；有一种研究认为，AQI监测指标中的二氧化硫（SO2），二氧化氮（NO2），一氧化碳（CO）是在一定环境条件下形成PM2.5前的主要气态物体。请依据附件1或附件2中的数据或自行采集数据，利用或建立适当的数学模型，对AQI中6个基本监测指标的相关与独立性进行定量分析，尤其是对其中PM2.5（含量）与其它5项分指标及其对应污染物（含量）之间的相关性及其关系进行分析。

看看附件1和附件2长啥样：

表1一个监测点，表2比较复杂，一张表里有十多个sheet，从分析来说肯定是表1比较方便，但是表1的数据没有表2多。
先从表1看起

import pandas as pd
data_train = pd.read_excel("附件1. 数据1.(武汉市一个监测点数据：2013.01.01-2013.08.26).xls")
data_train.info()

Data columns (total 11 columns):
日期 231 non-null datetime64[ns]
SO2 231 non-null int64
NO2 231 non-null int64
PM10 231 non-null int64
CO 231 non-null int64
O3 231 non-null int64
PM2.5 231 non-null int64
空气质量指数 231 non-null int64
首要污染物 215 non-null object
空气质量指数级别 231 non-null object
空气质量指数类别 231 non-null object
我要用的是SO2 、NO2、PM10、CO、O3、231、PM2.5 ，看起来数据都很正常。
将无关的特征丢掉，只剩下这六个先。

data_train.drop(['日期', '空气质量指数', '首要污染物', '空气质量指数级别', '空气质量指数类别'], axis=1, inplace=True)

6个基本监测指标间的相关性分析模型的建立与求解

然后来看看6个变量之间两两的相关系数

cor=data_train.corr() #相关系数矩阵，即给出了任意两个监测指标之间的相关系数print(cor)

SO2 NO2 PM10 CO O3 PM2.5
SO2 1.000000 0.799816 0.760169 0.644852 -0.176176 0.716012
NO2 0.799816 1.000000 0.833004 0.611555 -0.058873 0.726058
PM10 0.760169 0.833004 1.000000 0.640791 -0.033260 0.855680
CO 0.644852 0.611555 0.640791 1.000000 -0.382018 0.811476
O3 -0.176176 -0.058873 -0.033260 -0.382018 1.000000 -0.353722
PM2.5 0.716012 0.726058 0.855680 0.811476 -0.353722 1.000000

然后单独看看其余5个变量和PM2.5的相关系数

cor_pm25=data_train.corr()[u'PM2.5'] #只显示“PM2.5”与其他监测指标的相关系数
print(cor_pm25)

SO2 NO2 PM10 CO O3
PM2.5 0.742671 0.744698 0.858717 0.864230 -0.337372
可以看到PM10、CO 和PM2.5的相关性最大，O3为负相关，主要是对PM10、CO 和PM2.5进行分析.

看一下PM10与PM2.5的散点关系图

#PM2.5和PM10的散点图
import matplotlib.pyplot as plt
Y = data_train['PM2.5']
X = data_train['PM10']
plt.scatter(X, Y)
plt.xlabel("PM10")
plt.ylabel("PM2.5")
plt.show()

居然报错了，ValueError: could not convert string to float: '--'，值错误，string无法转换成float，错误字符为'--'，然后看下表
就懂了，散点图是要把表中的值都变成数值展示在散点图上，说明表上有'--'，仔细一看还真有。(上面是吹牛的，其实这个问题我思考了很久，才发现。。。。。。)

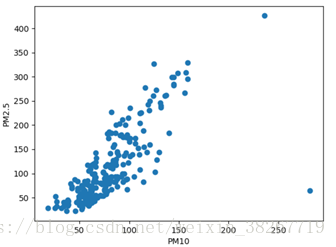
再看一下CO与PM2.5的散点关系图

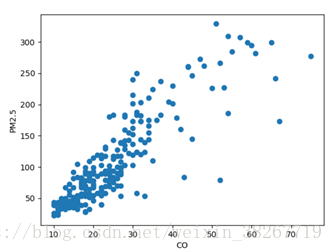
既然要定性来分析一下PM10、CO 和PM2.5的相关性，那就做一下拟合，包括一次线性、二次拟合、三次拟合，后来发现三次拟合的结果最好

#PM2.5和PM10做拟合
y = data_train['PM2.5']
x = data_train['PM10']
poly=np.polyfit(x,y,3)
plt.plot(x, y, 'o')
plt.plot(x, np.polyval(poly, x))
plt.show()

这里有个拟合优度的东西，公式是：

拟合结果是 [-4.93378118e-06 1.53713275e-03 1.15170538e+00 -8.67981674e+00]分别是三次、二次...的系数
求一下拟合优度

evaluate=np.polyval(poly, x)   #求拟合值
Rnew=1-math.sqrt(sum((y-evaluate)**2)/sum(y**2))
print(Rnew)

PM10与PM2.5拟合优度为: 0.7235192741702283

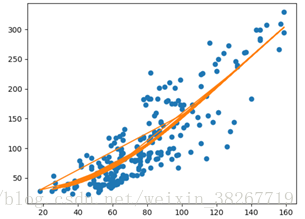
#PM2.5和CO做拟合
y = data_train['PM2.5']
x = data_train['CO']
poly=np.polyfit(x,y,3)
plt.plot(x, y, 'o')
plt.plot(x, np.polyval(poly, x))
evaluate=np.polyval(poly, x)   #求拟合值
Rnew=1-math.sqrt(sum((y-evaluate)**2)/sum(y**2))
print(Rnew)plt.show()

拟合结果：[ 2.05782732e-04 -3.07266314e-02 2.98834285e+00 5.49203122e+01]

CO与PM2.5拟合优度为: 0.725913270854075

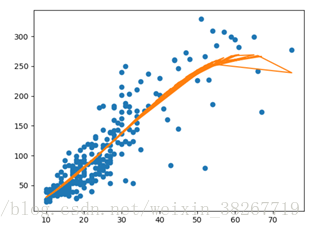
多元线性回归模型拟合

刚才是1对1，现在开始1对多的线性拟合了，主要是求回归系数，上代码

from sklearn import datasets,linear_model
import math
data_train=data_train.as_matrix()   #貌似dataframe不可以直接切片，所以先转化成array格式
regr = linear_model.LinearRegression()    
X = data_train[:,:4]  
y = data_train[:,5]   #第5列是PM2.5
regr.fit(X,y)
evaluate=regr.predict(X)
print(evaluate)
Rnew=1-math.sqrt(sum((y-evaluate)**2)/sum(y**2))
print(Rnew)    #同样是求拟合优度

拟合结果拟合优度：0.786566951522467
再对异常进行剔除(其实我不知道怎么剔除，我直接一对一来看散点图然后把不符合趋势的点去掉)
通过PM2.5与其他指标的散点图对异常点进行初步的剔除之后，得到拟合优度为0.8020336405286592

其实本文做的还是一些很基础的东西，主要还是对各种数据分析工具的熟悉。