同时标定激光和里程计

60 阅读 0 评论 40 点赞

我是靠谱客的博主无私大白，最近开发中收集的这篇文章主要介绍同时标定激光和里程计，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

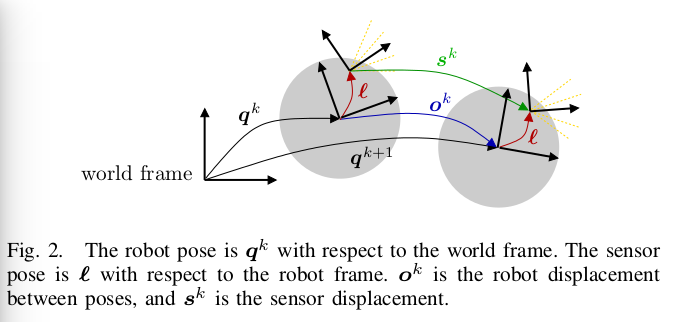
标定参数：两轮半径 $r_L,r_R$ ，两轮间距 $b$ ，传感器相对于机器人坐标系的位姿 $mathbf{l} = (l_x, l_y, l_theta)$

运动学模型：

$frac{d}{dt}begin{bmatrix} q_x(t)\ q_y(t) \ q_theta(t) end{bmatrix} = begin{bmatrix} v(t)cosq_theta(t)\ v(t)sinq_theta(t) \ omega (t) end{bmatrix} qquadqquad (1)$

其中:

$begin{bmatrix} v(t)\ omega (t) end{bmatrix} = boldsymbol{J}begin{bmatrix} omega _L(t)\ omega _R(t) end{bmatrix}, qquad J = begin{bmatrix} J_{11} & J_{12} \ J_{21} & J_{22} end{bmatrix} = begin{bmatrix} +r_L/2 & +r_R/2 \ -r_L/b & +r_R/b end{bmatrix} qquadqquad(2)$

假定在每次采样间隔内轮子速度恒定

$upsilon (t) = J_{11}omega _L^k + J_{12}omega _R^k = upsilon _0^k qquadqquad(3) \ omega (t) = J_{21}omega _L^k + J_{22}omega _R^k = omega _0^k qquadqquad(4)$

假设 $mathbf{q}^k = q(0) = mathbf{0}$ ，通过积分即可得到每个采样时刻的位姿

$mathbf{o}^k = begin{bmatrix} o_x^k \ o_y^k \ o_theta^k end{bmatrix} = begin{bmatrix} upsilon _0^kT^k(sinomega _0^kT^k)/(w_0^kT^k)\ upsilon _0^kT^k(1 - cosomega _0^kT^k)/(w_0^kT^k) \ omega _0^kT^k end{bmatrix} qquadqquad (5-7)$

估计 $J_{21}, J_{22}$ :

基于机器人旋转的角度 $o_theta^{k}$ 和传感器旋转的角度 $s_theta^k$ 相同的原理。由激光匹配得到的角度估计为 $hat{s}_theta^k$ ，里程计观测到的角度 $o_theta^k = omega _0^kT^k = (J_{21}omega _L + J_{22}omega _R)T^k$ 。

$begin{bmatrix} hat{omega }_L^kT^k & hat{omega }_R^kT^k end{bmatrix}begin{bmatrix} J_{21}\ J_{22} end{bmatrix} = hat{s}_theta^k + errors qquadqquad (8)$

所有时刻整合：

$begin{bmatrix} vdots & vdots \ hat{omega }_L^kT^k & hat{omega }_R^kT^k \ vdots & vdots end{bmatrix}begin{bmatrix} J_{21}\J_{22} end{bmatrix} = begin{bmatrix} vdots \ hat{s}_theta^k \ vdots end{bmatrix} + errors$

$J_{21},J_{22}$ 可以从上式中估计出来。

由于 $J_{21} = -r_L/b, J_{22} = -r_R/b$ ，因此还需估计 $b, l_x, l_y, l_theta$ 。

估计 $b, l_x, l_y, l_theta$ :

由图可知： $mathbf{l}oplus mathbf{s}^k = mathbf{o}^k oplusmathbf{l}$ ，展开：

$l_x + s_x^kcosl_theta - s_y^ksinl_theta = o_x^k + l_x coso_theta^k - l_ysino_theta^k qquad qquad (10)$

$l_y + s_x^ksinl_theta + s_y^kcosl_theta = o_y^k + l_x sino_theta^k + l_ycoso_theta^k qquad qquad (11)$

其中 $o_theta^k$ 已经估计出来。

将 $o_x^k, o_y^k$ 用其他参数表示：

$J_{11} = -frac{b}{2}J_{21}, J_{12} = frac{b}{2}J_{22}$

$upsilon _0^k = -frac{b}{2}J_{21}omega _L^k + frac{b}{2}J_{22}omega _R^k qquadqquad (12)$

将（12）代入（5-6）得到： $o_x^k = c_xb qquad o_y^k = c_yb qquadqquad (13)$

其中:

$c_x = frac{1}{2} T^k (-J_{21}omega _L^k + J_{22}omega _R^k)frac{sinomega _o^kT^k}{omega _0^kT^k}$

$c_y = frac{1}{2} T^k (-J_{21}omega _L^k + J_{22}omega _R^k)frac{1 - cosomega _o^kT^k}{omega _0^kT^k}$

将（13）代入（10）（11）中：

$l_x + s_x^kcosl_theta - s_y^ksinl_theta = c_xb + l_x coso_theta^k - l_ysino_theta^k qquad qquad (14)$

$l_y + s_x^ksinl_theta + s_y^kcosl_theta = c_yb + l_x sino_theta^k + l_ycoso_theta^k qquad qquad (15)$

定义： $mathbf{x} = begin{bmatrix} b & l_x & l_y & cosl_theta & sinl_theta end{bmatrix}^T$ ，额外约束： $x_4^2 + x_5^2 = 1$ 。

那么（14）（15）写成矩阵形式 $mathbf{L}_kmathbf{x} = mathbf{0}$ ：

$begin{bmatrix} -c_x & (1-coshat{o}_theta^k) & +sinhat{o}_theta^k & +hat{s}_x^k & -hat{s}_y^k\ -c_y & -sinhat{o}_theta^k & (1-coshat{o}_theta^k) & +hat{s}_x^k & +hat{s}_y^k end{bmatrix}$

定义： $mathbf{M} = sum ^k mathbf{L}_k^Tmathbf{L}^k$ ，解最小二乘问题：

$min mathbf{x}^Tmathbf{M}mathbf{x} qquadqquad (17) \ subject to x_4^2 + x_5^2 = 1 qquadqquad(18)$

由于对于任意解 $bar{mathbf{x}}$ ， $-bar{mathbf{x}}$ 同样是解。因此增加额外约束：

$x_1 > 0 qquad qquad qquad qquad (19)$

求解带约束的最小二乘问题:

使用拉格朗日乘子，将（18）约束写为矩阵形式：

$mathbf{x}^Tmathbf{W}mathbf{x} = 1, qquad with qquad mathbf{W}doteq begin{bmatrix} mathbf{0}_3times 3 & mathbf{0}_3times2 \ mathbf{0}_2times3 & mathbf{I}_3times2 end{bmatrix} qquad qquad qquad qquad (21)$

约束(19)暂时忽略，近采用当 $hat{x}_1$ 出现负值时跳过。

使用拉格朗日乘子方法，有：

$(mathbf{M} + lambda mathbf{W})mathbf{x} = mathbf{0}$

$lambda$ 求解： $det(mathbf{M}+lambda mathbf{M}) = 0$

$mathbf{M}$ 有比较特殊的结构：

$mathbf{M} = begin{bmatrix} m_{11} & 0 & m_{13} & m_{14} & m_{15} \ * & m_{22} & 0 & m_{35} & -m_{34} \ * & * & m_{22} & m_{34} & m_{35} \ * & * & * & m_{44} & 0 \ *& * & * & *& m_{44} end{bmatrix}$

$det(mathbf{M}+lambda mathbf{M})$ 是二次多项式 $(alambda ^2 +blambda +c)$ ，其中：

$a = m_{11}m_{22}^2 - m_{22}m_{13}^2$

$b = 2m_{13}m_{22}m_{35}m_{15} - m_{22}^2m_{15}^2 - 2m_{11}m_{22}m_{35}^2 \ qquad + 2m_{13}m_{22}m_{34}m_{14} - 2m_{22}m_{13}^2m_{44} - m_{22}^2m_{14}^2 \ qquad + 2m_{11}m_{22}^2m_{44} + m_{13}^2m_{35}^2 - 2m_{11}m_{22}m_{34}^2 \ qquad + m_{13}^2m_{34}^2$

$c = -2m_{13}m_{35}^3m_{15} - m_{22}m_{13}^2m_{44}^2 + m_{11}m_{22}^2m_{44}^2 \ + m_{13}^2m_{35}^2m_{44} + 2m_{13}m_{22}m_{34}m_{14}m_{44} \ + m_{13}^2m_{34}^2m_{44} - 2m_{11}m_{22}m_{34}^2m_{44} \ - 2m_{13}m_{34}^3m_{14} - 2m_{11}m_{22}m_{35}^2m_{44} \ +2m_{11}m_{35}^2m_{34}^2 + m_{22}m_{14}^2m_{35}^2 \ - 2m_{13}m_{35}^2m_{34}m_{14} - 2m_{13}m_{34}^2m_{35}m_{15} \ + m_{11}m_{34}^4 + m_{22}m_{15}^2m_{34}^2 \ + m_{22}m_{35}^2m_{15}^2 + m_{11}m_{35}^4 \ - m_{22}^2m_{14}^2m_{44} + 2m_{13}m_{22}m_{35}m_{15}m_{44} \ + m_{22}m_{34}^2m_{14}^2 - m_{22}^2m_{15}^2m_{44}$

由此求得 $bar{lambda}$ 。

对于任意 $det(mathbf{M}+bar{lambda} mathbf{M})$ 核空间的任意向量 $mathbf{upsilon}$ ，考虑（18）（19）约束，得到：

$hat{mathbf{x}} = frac{sign upsilon _1}{sqrt{upsilon _4^2 + upsilon _5^2}}mathbf{upsilon }$

最终标定参数为：

$hat{b} = hat{x}_1$

$hat{r}_L = hat{x}_1hat{J}_{21}$

$hat{r}_R = -hat{x}_1hat{J}_{22}$

$hat{l}_x = hat{x}_2$

$hat{l}_y = hat{x}_3$

$hat{l}_theta = atan2(hat{x}_5,hat{x}_4)$

参考链接：

https://blog.csdn.net/heyijia0327/article/details/85000943 贺博提供了代码