字节跳动三维视觉实习生（AR方向）字节跳动三维视觉（一面）

62 阅读 0 评论 41 点赞

我是靠谱客的博主隐形白羊，最近开发中收集的这篇文章主要介绍字节跳动三维视觉实习生（AR方向）字节跳动三维视觉（一面），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

字节跳动三维视觉（一面）

首先自我介绍，然后从简历上的项目开始阐述，之后便是从整个SLAM系统开始细挖（如下所述）

1. 为什么 $AX=0$ 使用 $SVD$ 分解后 $V$ 的最后一列是 $X$ 的解？

答：推导过程如下：

可以求取 $AX=0$ 的最小二乘解，因此问题转换为 ${min}left | AX right |displaystyle _{2}^{2}$ ，其中 $left | X right |_{2}=1$

利用SVD将A进行分解： $A=USigma V^{T}$ ，其中U，V为单位正交矩阵， $Sigma$ 为奇异值的对角矩阵。

则 $AX=USigma V^{T}X=0$ ，等式两边同乘 $U^{T}$ 可得， $Sigma V^{T}X=0$ ，（原因在于U为单位正交矩阵）。

则问题变为： ${min}left | AX right |displaystyle _{2}^{2}=minleft | Sigma V^{T}X right |_{2}^{2}$ ，取 $y=V^{T}X$ ，可得 ${min}left | AX right |displaystyle _{2}^{2}=minleft | Sigma V^{T}X right |_{2}^{2}=minleft | Sigma y |_{2}^{2}$

由于公式较多，因此采用手写的形式：

2. 牛顿法、高斯牛顿法、LM法、DogLeg方法的区别？

答：

最速下降法的本质： $x_{k+1}=x_{k}+alpha Delta x$

非线性优化的本质是：如何寻找合适的步长 $alpha$ 和梯度下降方向 $Delta x$ 。

下降方法分为：线搜索和信頼域的方式。其中线搜索需要先计算下降方向；而信頼域的方法则是通过划定一个区域范围，在该范围内直接确定下降位移。不需要计算下降方向

梯度下降法：沿着目标函数函数变小的方向运动，缺点是收敛速度慢，在收敛点附近波动。

牛顿法：目标函数二阶泰勒展开，缺点：由于需要计算H矩阵（Hessian矩阵），计算量大，但收敛速度较快。

高斯牛顿法：目标函数一阶泰勒展开，缺点：使用雅克比矩阵近似H矩阵 $H=J^{T}J$ ，但可能由于H矩阵不满秩导致算法无法收敛。

LM算法（最速下降法与高斯牛顿法的结合）：在高斯牛顿法的基础之上增加了可信赖区域，以解决H矩阵不满秩的问题， $H=J^{T}J+lambda I$ ，可以直接引入单位阵或者H矩阵的对角阵。收敛速度相对高斯牛顿较慢。可根据阻尼因子调节目标函数的下降速度和步长。注意：阻尼因子越大，越接近最速下降法；阻尼因子越小，越接近高斯牛顿法。其中阻尼因子根据比例因子来确定增大或者减少。

DogLeg算法（属于高斯牛顿与最速下降法结合）：信頼域的方法，没有采用上述的线搜索的方式。需要使用高斯牛顿法和最速下降算法分别计算迭代方向 $h_{gn}$ 和 $h_{sd}$ ，并计算最快下降法的迭代步长 $alpha =frac{left | g right |^{2}}{left | J(x)g right |^{2}}$

步骤5中选取DogLeg的下降步长，如下所示：

3. 本质矩阵、基础矩阵、单应矩阵

3.1 本质矩阵

本质矩阵：描述空间中的一个点，在不同视角下的几何约束关系（不同视角下的归一化坐标系），其约束关系是对极几何。仅与相机外参有关，与相机内参无关。

对极几何：空间中一点P同时被两个视角的图像所观测到，若在左图像的投影点为a，则在右图像的投影点b一定极线上。

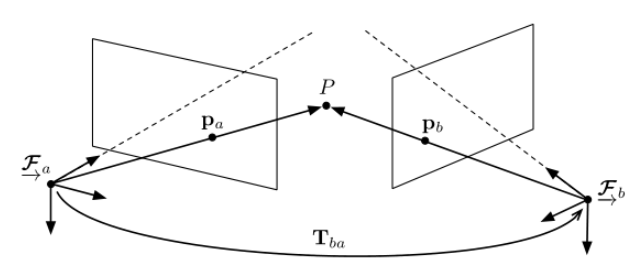
1. 本质矩阵推导过程如下：

已知：相机 $a$ 下的归一化坐标 $P$ ，相机a到相机b的坐标变换矩阵 $[R|t]$ 。

根据相机坐标系变换关系，可以得到相机 $b$ 下的归一化坐标 $P^{'}$ ，

$P^{'}=RP+t$

其中 $R,t$ 表示刚体的旋转和平移，对上式左叉乘一个 $t$ ，可得：

$ttimes P^{'}=ttimes (RP)+ttimes t=ttimes (RP)$

其中 $ttimes P^{'}$ 表示与 $t$ 和 $P^{'}$ 都垂直的向量（极平面的法向量），对上式左乘 $P^{'T}$ 得：

$P^{'T}(ttimes P^{'})=P^{'T}(ttimes RP)$

由于 $P^{'}$ 与 $ttimes P^{'}$ 垂直，所以有：

$0=P^{'T}(ttimes RP)=P^{'T}(ttimes R)P$

将上式的叉乘转换为向量的反对称矩阵与另一向量相乘，可化简为：

$P^{'T}(ttimes R)P=P^{'T}[t_{times}] RP$

其中 $[t_{times}]$ 表示反对称矩阵，取 $E=[t_{times}]R$ ，则可得：

$P^{'T}EP=0$

其中表示本质矩阵。其中 $P^{'}$ 与 $P$ 都是相机归一化坐标。

本质矩阵的秩为2，解释如下：

本质矩阵的自由度计算：

平移 $t$ 的待定参数是3，旋转矩阵的自由度是3，所以待定参数加起来是6，即要想确定矩阵，确定6个参数就够了，不用考虑矩阵的所有9个参数，同时E满足尺度等价性约束，所以的自由度是6-1=5.

（1）尺度等价性：对极约束的等式右侧为0，即乘以任意常数不改变两点间的变换关系。

2. 求解本质矩阵：

3. 对本质矩阵分解：

因为矩阵的秩等于非零奇异值的个数，因此本质矩阵 E 的奇异值必定是 [σ, σ, 0] T 的形式。

3.2 基础矩阵

基础矩阵：描述不同帧之间同一空间点像素坐标的几何约束关系。由本质矩阵约束中的归一化坐标替换为像素坐标点得到。

由本质矩阵可知：

$P^{'T}EP=0$

其中 $P^{'}$ 与 $P$ 都是相机归一化坐标，将其转换为像素坐标 $P^{'}=K^{-1}x^{'}$ 和 $P=K^{-1}x$ 。

$P^{'T}EP=x^{'T}K^{'-T}EK^{-1}x=0$

因此可取： $F=K^{'-T}EK^{-1}$ ，记为基础矩阵。

1. 基础矩阵自由度

基础矩阵的自由度为7， $F=K^{'-T}EK^{-1}$ ，左右相机内参的待定参数都为4，平移 $t$ 的待定参数为3，旋转矩阵的自由度为3，所以加起来 4+4+3+3=14个待定参数，但实际上矩阵的只有9个参数，同时F矩阵满足尺度等价性和秩为2（行列式为0，方阵不满秩其行列式为0），因此矩阵的自由度为9-2=7.

3.3 单应矩阵

单应矩阵：描述处于共同平面上的一些点在两张图像之间的变换关系。

1. 单应矩阵的推导

表示不同相机下的像素坐标的变换关系。

4. VINS-Mono为什么要是用预积分？

答：

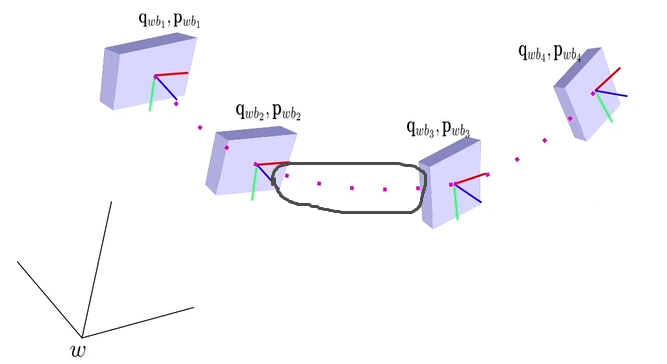
由公式28可知，时刻的位姿是由 $[i,j]$ 时间段内所有的 $q_{wb_{t}}$ 积分而来，即满足马尔科夫链的关系。如果 $q_{wb_{t}}$ 被后端所优化更新，该时间段内的所有状态变量（世界坐标系下）都需要重新进行积分，计算量很大。因此可将积分模型转换为预积分模型，如上图所示，直接变为求解黑色圈内的积分量即可，公式如下：

$q_{wbt}=q_{wbi} otimes q_{bibt}$

4.1 IMU的预积分误差

利用上述的预积分过程可以求出时刻的 $P,V,Q,Ba,Bg$ 。因此便可以利用是积分等式两端做差求得预积分误差。

其中IMU构建的预积分量作为测量值，优化变量是时刻的 $P,V,Q,Ba,Bg$ 。

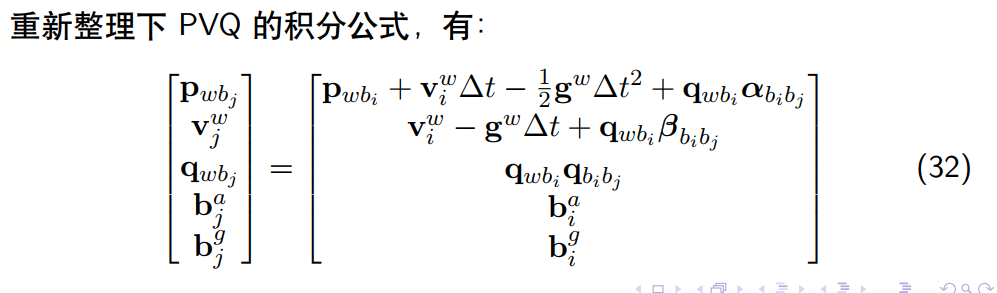
5. VINS-Mono整体流程

答：VINS-Mono可以分为四大模块：视觉跟踪前端、后端非线性优化（IMU预积分、初始化）、闭环检测、闭环优化。

5.1 视觉跟踪前端

首先对第一帧图像进行自适应直方图均衡化，并使用Shi-Tomasi提取150个特征点，设置非极大值抑制半径为30，为每个特征点设置新的id号。对于接下来的图像帧，使用KLT进行光流跟踪，并将跟踪上的特征点进行计数。然后，对特征点进行畸变校正（原因在于图像本身存在畸变，但没有对图像矫正畸变，而是对特征点校正畸变。设置相机的畸变模型），将校正畸变后的特征点使用RANSAC进行剔除。最后判断当前跟踪的特征点是否少于150个，如果少于150个则需要在特征点的mask之外，使用Shi-Tomasi提取新的特征点，以补足150个。

最后将提取的特征点像素坐标投影到归一化平面上，发布出去。之后也是一帧一帧跟踪下去。

5.2 后端非线性优化

5.2.1 IMU预积分

获取两帧图像间的IMU数据（根据时间戳进行对齐，只取两帧图像间的IMU数据），将获取到的IMU数据（角速度、加速度）进行预积分（中值积分），同时积分计算当前时刻的body位姿预测值（由积分得到）。同时计算预积分误差的雅克比矩阵和协方差矩阵，用于后端优化的IMU误差项。其中IMU预积分误差可见上文。优化变量为时刻的 $P, V,Q, Ba, Bg$ 。

5.2.2 初始化

先根据视差量判断当前帧是否为关键帧，如果存在足够的视差则设置为关键帧，否则不是关键帧；如果是关键帧则将滑窗内的最老帧删除掉，否则直接扔掉当前帧的视觉测量，仅保留IMU测量值。

判断滑窗内的图像帧数是否达到10个，如果达到开始进行初始化过程。

relativePose：在滑窗内寻找与当前帧（滑窗的最后一帧）匹配特征点较多且视差量较大的关键帧作为参考帧，并通过基础矩阵计算当前帧到参考帧的变换矩阵；
globalSFM：首先三角化参考帧与当前帧之间的路标点，并利用PnP求解某一帧（参考帧与当前帧之间）的位姿；再三角化参考帧与某一帧之间的路标点；之后PnP求解第一帧与参考帧之间的某一帧的位姿，并三角化该帧到参考帧的路标点；三角化其他未恢复的路标点； BA优化滑窗内的所有位姿。
solvePnP：利用SFM得到的所有3D路标点，求解出世界坐标到相机坐标的变换；
visualInitialAlign：利用视觉相邻间的旋转应等于IMU预积分的旋转值去校正陀螺仪bias；初始化速度、重力向量g和尺度因子，优化重力方向

5.2.3 后端优化 solveOdometry

后端优化是VINS-Mono中除了初始化之外，创新性最高的一块，也是真真的 紧耦合 部分，而初始化的过程事实上是一个 松耦合。因为初始化过程中的状态量并没有放在最底层融合，而是各自做了位姿的计算，但是在后端优化的过程中，所有优化量都是在一起的。

注意：在solveOdometry中先进行特征点三角化，然后在送入BA求解位姿。

f_manager.triangulate(Ps, tic, ric); 利用的是IMU积分得到的位姿（ $T_{wi}$ ）与相机IMU外参矩阵得到相机到世界坐标系的位姿，从而使用三角化进行估计特征点深度。

使用ceres构建全局BA优化模型，误差函数包括：边缘化先验约束、IMU预积分误差、视觉重投影误差、闭环约束误差；然后开始进行BA优化位姿。

视觉重投影误差：已知一对匹配的特征点（归一化坐标），特征点逆深度（三角化得到）。可以将第帧图像的特征点变换到相机坐标系下，在变换为imu坐标系下，之后变换到世界坐标系下，最后反变换到第帧IMU坐标系下，相机坐标系、图像坐标系；从而构建为视觉重投影误差，最后的优化变量就是该过程中的逆深度和各个坐标下的位姿。优化变量个数：特征点逆深度 $lambda _{i}$ ，第帧相机位姿 $T_{wi}$ ，第帧相机位姿 $T_{wj}$ ，相机IMU位姿 $T_{bc}$

5.2.4 边缘化marginalization

边缘化(marginalization)的过程就是将滑窗内的某些较旧或者不满足要求的视觉帧剔除的过程，所以边缘化也被描述为将联合概率分布分解为边缘概率分布和条件概率分布的过程(说白了，就是利用shur补减少优化参数的过程)。

直接进行边缘化而不加入先验条件的后果：

无故地移除这些pose和feature会丢弃帧间约束，会降低了优化器的精度，所以在移除pose和feature的时候需要将相关联的约束转变为一个先验的约束条件作为prior放到优化问题中
在边缘化的过程中，不加先验的边缘化会导致系统尺度的缺失(参考[6])，尤其是系统在进行__退化运动__时(如无人机的悬停和恒速运动)。一般来说只有两个轴向的加速度不为0的时候，才能保证尺度可观，而退化运动对于无人机或者机器人来说是不可避免的。所以在系统处于退化运动的时候，要加入先验信息保证尺度的客观性。

Shur补消元：

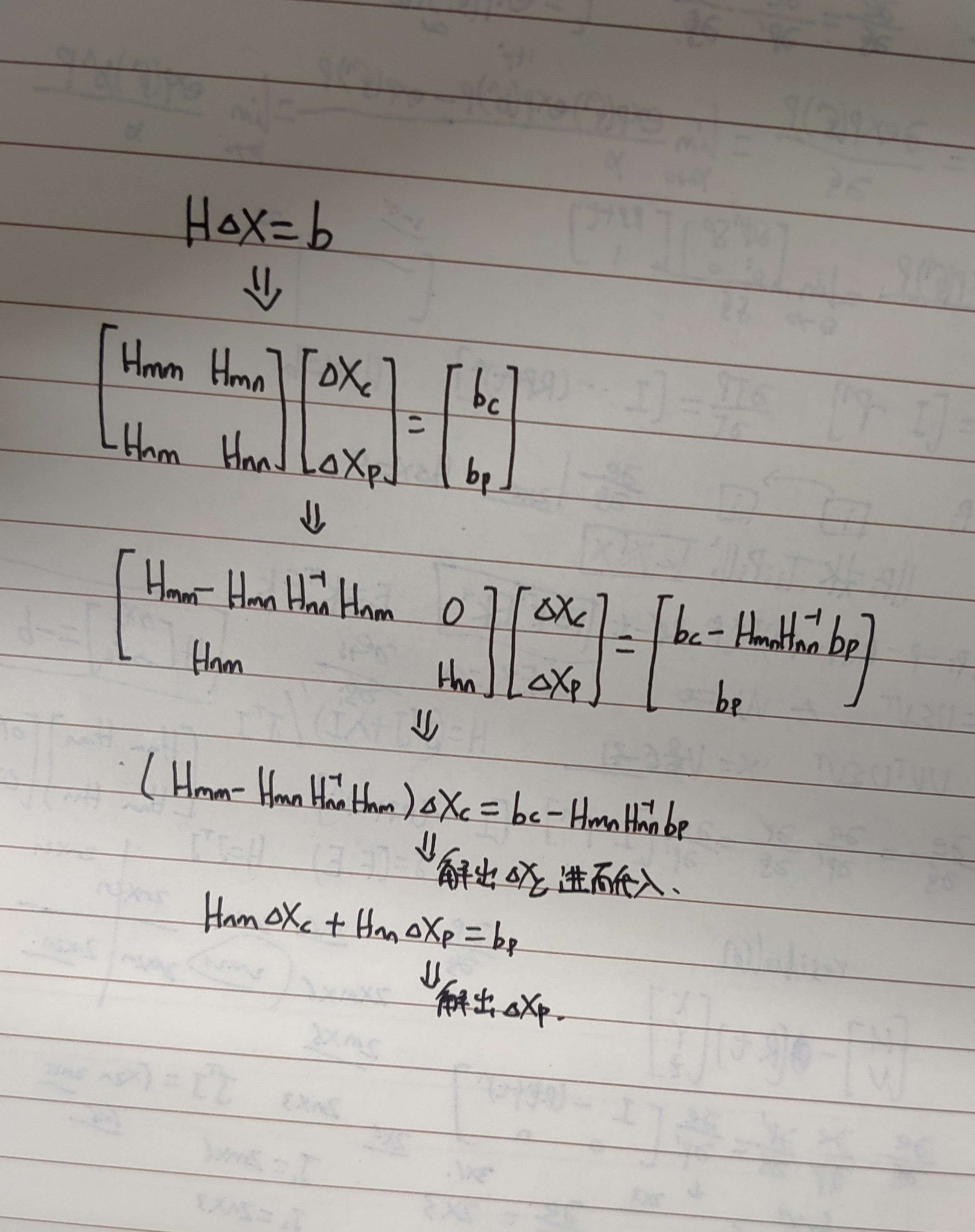
5.2.5 滑窗优化slideWindow

按理说是不应该把滑窗当做一小节来讲的，边缘化、舒尔补都属于滑窗的范围，但前面已经总结了。滑窗的三大法宝"Marginalization"，"Schur complement"，"First estimate jacobin"

5.3 闭环检测和优化

Vins-Mono还是利用词袋的形式来做Keyframe Database的构建和查询。在建立闭环检测的数据库时，关键帧的Features包括两部分：VIO部分的200个强角点和500 Fast角点。然后描述子仍然使用BRIEF(因为旋转可观，匹配过程中对旋转有一定的适应性，所以不用使用ORB)。

在闭环检测成功之后，会得到回环候选帧。所以要在已知位姿的回环候选帧和滑窗内的匹配帧做匹配，然后把回环帧加入到滑窗的优化当中，这时整个滑窗的状态量的维度是不发生变化的，因为回环帧的位姿是固定的。

因为之前做的非线性优化本质只是在一个滑窗之内求解出了相机的位姿，而且在回环检测部分，利用固定位姿的回环帧只是纠正了滑窗内的相机位姿，并没有修正其他位姿(或者说没有将回环发现的误差分配到整个相机的轨迹上)，缺少全局的一致性，所以要做一次全局的Pose Graph。全局的Pose Graph较之滑窗有一定的迟滞性，只有相机的Pose滑出滑窗的时候，Pose才会被加到全局的Pose Graph当中。

6. 编程题

给定一组无序数组，该数组中包含重复数字，请查找出该数组中的所有重复数字。

vector<int> Sloution(vector<int> number)
{
    map<int, int> map_x;
    vector<int> res;

    for(int i=0; i<number.size(); i++)
    {
       if( ++map_x[number[i]] == 2) res.push_back(number[i]);
    }

    return res;
}

最后

以上就是隐形白羊为你收集整理的字节跳动三维视觉实习生（AR方向）字节跳动三维视觉（一面）的全部内容，希望文章能够帮你解决字节跳动三维视觉实习生（AR方向）字节跳动三维视觉（一面）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：实习专栏
浏览次数：62 次浏览
发布日期：2024-01-16 10:31:15
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_23_ogf4_13__7_gz.html

字节跳动三维视觉实习生（AR方向）字节跳动三维视觉（一面）

概述

字节跳动三维视觉（一面）

首先自我介绍，然后从简历上的项目开始阐述，之后便是从整个SLAM系统开始细挖（如下所述）

1. 为什么 $AX=0$ 使用 $SVD$ 分解后 $V$ 的最后一列是 $X$ 的解？

2. 牛顿法、高斯牛顿法、LM法、DogLeg方法的区别？