1、什么是熵权法

一种客观赋值法，确定样本每个指标的权重。涉及到信息量信息熵的个概念可以去这里查看

1.1 优点

• 熵权法能深刻反应指标的区分能力，确定较好的权重
• 赋权更加客观，有理论依据，可信度也更加高
• 算法简单，实践，不需要其他软件分析

1.2 缺点

• 无法考虑到指标与指标之间的横向影响
• 对样本依赖性大，随建模样本变化，权重也会发生变化
• 可能导致权重失真，最终结果无效。

1.3 适用范围

单单使用熵值法权重失真是经常发生的，要结合一定专家打分法才能发挥熵值法的优势。上层可能需要结合专家经验来构建，而底层的指标分的比较细，权重比较难确定，这种情况下采用熵值法比较合适。

另外，确定权重前需要确定指标对目标得分的影响方向，对非线性的指标要进行预处理或者剔除。还要注意处理好极值。

2、使用熵权法过程

2.1 数据预处理

2.1.1清洗指标极值

原则：剔除占样本总数不到1-2%但指标值贡献率超过20-30%以上的极值样本。大大增加样本的变异程度，但实际上却没有起到很大的作用。

2.1.2 归一化指标处理

假设对 n个样本， m个指标，则 $x_{ij}$ 为第 i 个样本的第 j 个指标的数值（ $i=1,...,n,j=1,...,k$）

2.1.2.1 临界值法

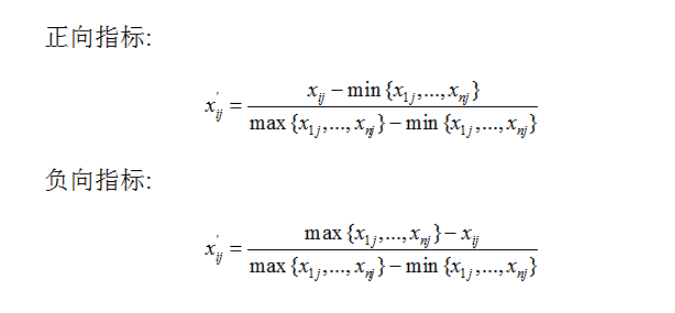
2.1.2.2 Z-score法

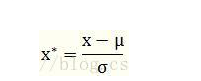
2.2 计算第项指标下第i个样本值占该指标的比重

$$p_{ij}=Y_{ij}/\sum _{i=1}^n{Y}_{ij}$$

2.3 计算第j项指标的熵值

$$E_j=-\sum _{i=1}^n{p}_{ij}\times lo{g}_2(p_{ij})$$

2.4 计算各项指标的权重

各项指标的信息熵为
$E_1,E_2,...,E_k$

通过信息熵计算各指标的权重
$$W_i=\frac{1-E_i}{k-\sum E_i}(i=1,2,...,k)$$

3、实例

import pandas as pd
import numpy as np
import math
from numpy import array
from sklearn.preprocessing import MinMaxScaler
from sklearn.datasets import load_iris

# 1读取数据,使用sklearn自带的鸢尾数据集
iris = load_iris()
x = iris.data
df = pd.DataFrame(x)

# 2数据预处理 ,去除空值的记录
df.dropna(inplace=True)

# 定义熵权法函数
def cal_weight(x):
    Scaler = MinMaxScaler().fit(x)
    '''熵值法计算变量的权重'''
    # 标准化
    x = Scaler.transform(x)

    # 求k
    rows = x.shape[0]  # 行
    cols = x.shape[1]  # 列
    k = 1.0 / math.log(rows)

    # 矩阵计算--
    # 信息熵
    # p=array(p)
    x = array(x)
    lnf = [[None] * cols for i in range(rows)]
    lnf = array(lnf)
    for i in range(0, rows):
        for j in range(0, cols):
            if x[i][j] == 0:
                lnfij = 0.0
            else:
                p = x[i][j] / x.sum(axis=0)[j]
                lnfij = math.log(p) * p * (-k)
            lnf[i][j] = lnfij
    lnf = pd.DataFrame(lnf)
    E = lnf

    # 计算冗余度
    d = 1 - E.sum(axis=0)

    # 计算各指标的权重
    w = np.zeros((x.shape[1],))

    for j in range(cols):
        wj = d[j] / sum(d)
        w[j] = wj
        # 计算各样本的综合得分,用最原始的数据

    w = pd.DataFrame(w)
    return w


if __name__ == '__main__':
    # 计算df各字段的权重
    w = cal_weight(df)  # 调用cal_weight
    w.index = iris.feature_names
    w.columns = ['weight']
    print(w)

4、参考资料

https://hujichn.github.io/2016/08/10/熵值法确定权重的步骤及适用范围/

https://blog.csdn.net/starter_____/article/details/82086090

最后

以上就是平常豌豆为你收集整理的（1）评价算法—熵权法1、什么是熵权法2、使用熵权法过程3、实例4、参考资料的全部内容，希望文章能够帮你解决（1）评价算法—熵权法1、什么是熵权法2、使用熵权法过程3、实例4、参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。