一、熵的概念与定义

• 熵概念
    熵，在信息论中是用来刻画信息混乱程度的一种度量。熵最早源于热力学，后应广泛用于物理、化学、信息论等领域。1850年，德国物理学家鲁道夫·克劳修斯首次提出熵的概念，用来表示任何一种能量在空间中分布的均匀程度。1948年，Shannon在Bell System Technical Journal上发表文章“A Mathematical Theory of Communication”，将信息熵的概念引入信息论中。本文所说的熵就是Shannon熵，即信息熵，解决了对信息的量化度量问题。
  

• 熵定义
  针对一随机变量X，其熵表达式为
  $$H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i$$
  其中，
    n 代表X的n种不同的离散取值；
    $p_i$ 代表了X取值为i的概率；
    log 为以2或者e为底的对数
   从定义中可以看出变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。

二、python 实现

• 数据集引用：信息熵及其Python的实现，结果与该文章一致。

• 数据集
  [1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 1, 2, 3, 4, 5 ]

• 引文结果：
  

• 本文结果
  

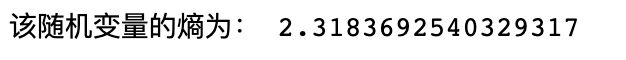
• 本文代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import math
from collections import Counter

def Entropy(DataList):
    '''
        计算随机变量 DataList 的熵
    '''
    counts = len(DataList)      # 总数量
    counter = Counter(DataList) # 每个变量出现的次数
    prob = {i[0]:i[1]/counts for i in counter.items()}      # 计算每个变量的 p*log(p)
    H = - sum([i[1]*math.log2(i[1]) for i in prob.items()]) # 计算熵
    
    return H

if __name__ == "__main__":
    data_list = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 1, 2, 3, 4, 5 ]
    HX = Entropy(data_list)
    print("该随机变量的熵为：",HX)

• 参考1：信息熵及其Python的实现
• 参考2：python 重复统计与常用去重（列表list、dataframe）（该文章中的列表重复统计）
• 参考3：能否尽量通俗地解释什么叫做熵

最后

以上就是勤恳老虎最近收集整理的关于python 信息熵一、熵的概念与定义二、python 实现的全部内容，更多相关python内容请搜索靠谱客的其他文章。