解耦原子范数最小化

解耦原子范数最小化(DANM)的产生

首先，定义一个矩阵形式（与其对应的是向量形式）的原子集：
A = { a x ( θ ) a y H ( θ ) : θ ∈ [ − π 2 , π 2 ] , a x ( θ ) ∈ C N × 1 , a y ( θ ) ∈ C M × 1 } mathcal{A}={boldsymbol{a}_x(theta)boldsymbol{a}_y^H(theta):thetain[-frac{pi}{2},frac{pi}{2}],boldsymbol{a}_x(theta)inmathbb{C}^{Ntimes1},boldsymbol{a}_y(theta)inmathbb{C}^{Mtimes1}} A={ax​(θ)ayH​(θ):θ∈[−2π​,2π​],ax​(θ)∈CN×1,ay​(θ)∈CM×1}
在DOA估计问题中，${\mathbf{a}}_x(\theta ),{\mathbf{a}}_y(\theta )$分别表示两条阵列的方向向量，$\mathbf{Z}\in {\mathbb{C}}^{N\times M}$往往表示两个阵列的互协方差矩阵。那么，具体的解耦原子范数为：
∥ Z ∥ A = inf ⁡ { ∑ k ∣ s k ∣ : Z = ∑ k s k a x ( θ k ) a y H ( θ k ) , a x ( θ k ) a y H ( θ k ) ∈ A } |boldsymbol{Z}|_mathcal{A}=inf{sum_{k}|s_k|:boldsymbol{Z}=sum_{k}s_kboldsymbol{a}_x(theta_k)boldsymbol{a}_y^H(theta_k),boldsymbol{a}_x(theta_k)boldsymbol{a}_y^H(theta_k)inmathcal{A}} ∥Z∥A​=inf{k∑​∣sk​∣:Z=k∑​sk​ax​(θk​)ayH​(θk​),ax​(θk​)ayH​(θk​)∈A}
与$l_1$原子范数最小化(ANM)类似，解耦原子范数最小化问题表述为：
$$\begin{gathered} \underset{\mathbf{Z}}{\min }\Vert \mathbf{Z}{\Vert }_{\mathcal{A}} \\ s.t\Vert \mathbf{Z}-\hat{\mathbf{Z}}\Vert \le \eta \end{gathered}$$
该问题可以转换为半正定规划(SDP)问题。

转化为SDP问题

证明内容在下一节，转化后的SDP问题表述为：

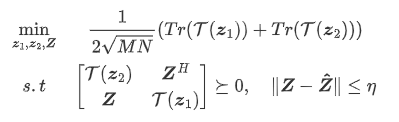
转化为该SDP问题的过程中，有以下前提（达到其中一个就可），是不可忽略的。
$$\begin{gathered} {\Delta }_x=\underset{i\ne j}{\min }|f_{x,i}-f_{x,j}|\ge \frac{1}{\lfloor (N-1)/4\rfloor } \\ {\Delta }_y=\underset{i\ne j}{\min }|f_{y,i}-f_{y,j}|\ge \frac{1}{\lfloor (M-1)/4\rfloor } \end{gathered}$$
在上式中，第k个信号在x阵列和y阵列上相邻的阵元间产生的相位差分别为：$2\pi f_{x,k}$和$2\pi f_{x,k}$，其方向向量亦可表述为：${\mathbf{a}}_x(f_k)$和${\mathbf{a}}_y(f_k)$。$\mathcal{T}(\mathbf{z})$表示以向量$\mathbf{z}$产生一个同尺寸的Hermitian-Toeplitz矩阵。

SDP问题转化的证明

在忽略变量$\mathbf{Z}$的情况下，定义目标函数为：
$$g({\mathbf{z}}_1,{\mathbf{z}}_2)=\frac{1}{2\sqrt{MN}}\left(Tr(\mathcal{T}({\mathbf{z}}_1))+Tr(\mathcal{T}({\mathbf{z}}_2))\right)$$
其中，
$$({\mathbf{z}}_1,{\mathbf{z}}_2)\in {\mathcal{S}}_{\mathbf{Z}}^{+}=\left\{({\mathbf{z}}_1,{\mathbf{z}}_2):\left[\begin{array}{cc}\mathcal{T}({\mathbf{z}}_2)& {\mathbf{Z}}^H\\ \mathbf{Z}& \mathcal{T}({\mathbf{z}}_1)\end{array}\right]⪰0\right\}$$
所以，要证明以上优化问题的等效，只需证明以下等式即可。
$$g^{\ast }=\underset{({\mathbf{z}}_1,{\mathbf{z}}_2)\in {\mathcal{S}}_{\mathbf{Z}}^{+}}{\min }g({\mathbf{z}}_1,{\mathbf{z}}_2)=\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$$
先证明$g^{\ast }\le \Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$成立。

引理1：如果数据矩阵$\mathbf{Z}\in {\mathbb{C}}^{N\times M}$在$f$上足够可分，即在原子集$\mathcal{A}$中，有足够多的原子${\mathbf{a}}_x(f){\mathbf{a}}_y^H(f)$。那么，当数据矩阵$\mathbf{Z}$确定时，它就有唯一的稀疏原子分解。在此情况下，得到了：
$$\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}=\sum _k|s_k|$$

在引理1的条件下，直接写出数据矩阵$\mathbf{Z}$的唯一原子分解为：
$$\mathbf{Z}=\sum _k{s}_k{\mathbf{a}}_x(f_k){\mathbf{a}}_y^H(f_k)$$
直接构造矩阵$\mathcal{T}({\tilde{\mathbf{z}}}_1)$和$\mathcal{T}({\tilde{\mathbf{z}}}_2)$：
$$\begin{gathered} \mathcal{T}({\tilde{\mathbf{z}}}_1)=\sum _k\sqrt{\frac{M}{N}}|s_k|{\mathbf{a}}_x(f_k){\mathbf{a}}_x^H(f_k) \\ \mathcal{T}({\tilde{\mathbf{z}}}_2)=\sum _k\sqrt{\frac{N}{M}}|s_k|{\mathbf{a}}_y(f_k){\mathbf{a}}_y^H(f_k) \end{gathered}$$
显然，它们都是Hermitian-Toeplitz矩阵，分别将$\mathbf{Z},\mathcal{T}({\tilde{\mathbf{z}}}_1),\mathcal{T}({\tilde{\mathbf{z}}}_2)$代入约束条件中，得到：
$$\left[\begin{array}{cc}\mathcal{T}({\tilde{\mathbf{z}}}_2)& {\mathbf{Z}}^H\\ \mathbf{Z}& \mathcal{T}({\tilde{\mathbf{z}}}_1)\end{array}\right]=\sum _k\frac{|s_k|}{\sqrt{MN}}\left[\begin{array}{c}\sqrt{N}{\mathbf{a}}_y(f_k)\\ sign(s_k)\sqrt{M}{\mathbf{a}}_x(f_k)\end{array}\right]{\left[\begin{array}{c}\sqrt{N}{\mathbf{a}}_y(f_k)\\ sign(s_k)\sqrt{M}{\mathbf{a}}_x(f_k)\end{array}\right]}^H⪰0$$
上式成立，说明向量${\tilde{\mathbf{z}}}_1$和${\tilde{\mathbf{z}}}_2$是$g({\mathbf{z}}_1,{\mathbf{z}}_2)$的一组可行解，代入目标函数中，得到：
$$g({\tilde{\mathbf{z}}}_1,{\tilde{\mathbf{z}}}_2)=\frac{1}{2\sqrt{MN}}\left(Tr(\mathcal{T}({\tilde{\mathbf{z}}}_1))+Tr(\mathcal{T}({\tilde{\mathbf{z}}}_2))\right)=\sum _k|s_k|$$
巧了，${\sum }_k|s_k|=\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$刚好成立，$g$的可行解对应着$\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$，那么，$g$的最优解$g^{\ast }$必然小于可行解，即：
$$g^{\ast }\le g({\tilde{\mathbf{z}}}_1,{\tilde{\mathbf{z}}}_2)=\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$$
得证。

接下来，再证明$g^{\ast }\ge \Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$成立。
此时，引入一个新的原子集，叫做“多测量向量(MMV)原子集”，它有如下的定义：
A x = { a x ( f ) e M H : ∀ f ∈ [ 0 , 1 ] , ∀ e M ∈ C M × 1 , ∥ e M ∥ = 1 } mathcal{A_x}={boldsymbol{a}_x(f)boldsymbol{e}^H_M:forall fin [0,1],forall boldsymbol{e}_Minmathbb{C}^{Mtimes 1},|boldsymbol{e}_M|=1 } Ax​={ax​(f)eMH​:∀f∈[0,1],∀eM​∈CM×1,∥eM​∥=1}
对于MMV问题，它有以下有用的结论：

引理2：对于任意的一个能够在MMV原子集上线性可分的数据矩阵$\mathbf{Z}\in {\mathbb{C}}^{N\times M}$，它在${\mathcal{A}}_x$上的原子范数可由以下SDP问题算出：
$$\Vert \mathbf{Z}{\Vert }_{{\mathcal{A}}_x}=\underset{\mathbf{V},\mathbf{z}}{\min }\left\{\frac{1}{2\sqrt{N}}(Tr(\mathbf{V})+Tr(\mathcal{T}(\mathbf{z})))\right\}s.t\left[\begin{array}{cc}\mathbf{V}& {\mathbf{Z}}^H\\ \mathbf{Z}& \mathcal{T}(\mathbf{z})\end{array}\right]⪰0$$
其中，$\mathbf{V}\in {\mathbb{C}}^{M\times M}$是一个Hermitian矩阵，$\mathcal{T}(\mathbf{z})\in {\mathbb{C}}^{N\times N}$是一个Toeplitz矩阵。

引理3：如果$\mathbf{Z}={\sum }_k{s}_k{\mathbf{a}}_x(f_k){\mathbf{e}}_M^H$，${\mathbf{a}}_x(f_k){\mathbf{e}}_M^H$是MMV集合中的原子，满足以下的频率可分条件：
$${\Delta }_x=\underset{i\ne j}{\min }|f_{x,i}-f_{x,j}|\ge \frac{1}{\lfloor (N-1)/4\rfloor }$$
那么，就可以保证：
$$\Vert \mathbf{Z}{\Vert }_{{\mathcal{A}}_x}=\sum _k|s_k|$$
这一点也正好对应了转换成SDP问题的前提条件。

有了这两个引理做铺垫，我们就可以完成证明。
不失一般性的，我们考虑x轴满足前提条件：
$${\Delta }_x=\underset{i\ne j}{\min }|f_{x,i}-f_{x,j}|\ge \frac{1}{\lfloor (N-1)/4\rfloor }$$
根据引理1，在解耦原子范数集$\mathcal{A}$下，它有唯一的分解为：
$$\begin{array}{rl}\mathbf{Z}=\sum _k{s}_k{\mathbf{a}}_x(f_k){\mathbf{a}}_y^H(f_k)& =\sum _k{s}_k\Vert {\mathbf{a}}_y^H(f_k){\Vert }_2{\mathbf{a}}_x(f_k)\frac{{\mathbf{a}}_y^H(f_k)}{\Vert {\mathbf{a}}_y^H(f_k){\Vert }_2}\\ & =\sum _k(\sqrt{M}{s}_k){\mathbf{a}}_x(f_k)\frac{{\mathbf{a}}_y^H(f_k)}{\Vert {\mathbf{a}}_y^H(f_k){\Vert }_2}\end{array}$$
显然，$\frac{{\mathbf{a}}_x(f_k){\mathbf{a}}_y^H(f_k)}{\Vert {\mathbf{a}}_y^H(f_k){\Vert }_2}\in {\mathcal{A}}_x$。另外，由于引理3，所以可以将其MMV原子范数表示为：
$$\Vert \mathbf{Z}{\Vert }_{{\mathcal{A}}_x}=\sqrt{M}\sum _k|s_k|$$
同时，
$$\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}=\sum _k|s_k|$$
因此，数据矩阵$\mathbf{Z}$的两种原子范数的联系就建立起来了：
$$\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}=\frac{1}{\sqrt{M}}\Vert \mathbf{Z}{\Vert }_{{\mathcal{A}}_x}$$
由于引理2，那么，取$\mathbf{V}=\mathcal{T}({\mathbf{z}}_2)$，$\mathbf{z}={\mathbf{z}}_1$，
∥ Z ∥ A = min ⁡ z 1 , z 2 { 1 2 M N ( T r ( T ( z 1 ) ) + T r ( T ( z 2 ) ) ) } = min ⁡ z 1 , z 2 g ( z 1 , z 2 ) ≤ { g ( z ~ 1 , z ~ 2 ) : ( z ~ 1 , z ~ 2 ) ∈ S Z + } begin{aligned} |boldsymbol{Z}|_{mathcal{A}}=&min_{boldsymbol{z_1},boldsymbol{z_2}}left{frac{1}{2sqrt{MN}}(Tr(mathcal{T}(boldsymbol{z_1}))+Tr(mathcal{T}(boldsymbol{z_2}))) right}=min_{boldsymbol{z_1},boldsymbol{z_2}}{g(boldsymbol{z_1},boldsymbol{z_2})} \ leq & {g(boldsymbol{tilde{z}}_1,boldsymbol{tilde{z}}_2):(boldsymbol{tilde{z}}_1,boldsymbol{tilde{z}}_2) in mathcal{S}_{boldsymbol{Z}}^{+}} end{aligned} ∥Z∥A​=≤​z1​,z2​min​{2MN ​1​(Tr(T(z1​))+Tr(T(z2​)))}=z1​,z2​min​g(z1​,z2​){g(z~1​,z~2​):(z~1​,z~2​)∈SZ+​}​
上式最后一项是可行解对应的目标集，由于$g^{\ast }$也是可行解对应的目标之一，所以，
$$\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}\le g^{\ast }$$
证毕。

$$\underset{({\mathbf{z}}_1,{\mathbf{z}}_2)\in {\mathcal{S}}_{\mathbf{Z}}^{+}}{\min }g({\mathbf{z}}_1,{\mathbf{z}}_2)=\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}$$
结论得证。因而，当数据矩阵$\mathbf{Z}$不确定时，关于它的优化问题等价为：
$$\underset{\mathbf{Z}}{\min }\underset{({\mathbf{z}}_1,{\mathbf{z}}_2)\in {\mathcal{S}}_{\mathbf{Z}}^{+}}{\min }g({\mathbf{z}}_1,{\mathbf{z}}_2)=\underset{\mathbf{Z}}{\min }\Vert \mathbf{Z}{\Vert }_{\mathcal{A}}=\underset{{\mathbf{z}}_1,{\mathbf{z}}_2,\mathbf{Z}}{\min }g({\mathbf{z}}_1,{\mathbf{z}}_2)s.t\left[\begin{array}{cc}\mathcal{T}({\mathbf{z}}_2)& {\mathbf{Z}}^H\\ \mathbf{Z}& \mathcal{T}({\mathbf{z}}_1)\end{array}\right]⪰0$$
等价问题得证。

参考文献和博客

下载参考文献
提取码：6666
博客：原子范数最小化参考博客

最后

以上就是发嗲小土豆最近收集整理的关于解耦原子范数最小化(Decoupled Atomic Norm Minimization)解耦原子范数最小化SDP问题转化的证明参考文献和博客的全部内容，更多相关解耦原子范数最小化(Decoupled内容请搜索靠谱客的其他文章。