简 介：
关键词： 矩阵，分解，QR
§01 矩阵的迹
1.1 定义
- 参考文献： Trace of a matrix
对于方形矩阵 A A A 是一个 K × K K times K K×K 的矩阵，它的迹，记为 t r a c e ( A ) traceleft( A right) trace(A) ，或者 t r ( A ) trleft( A right) tr(A) 定义为矩阵对角线元素累加和： t r ( A ) = ∑ k = 1 K A k k trleft( A right) = sumlimits_{k = 1}^K {A_{kk} } tr(A)=k=1∑KAkk 。
例如下面的矩阵：
A
=
[
2
1
5
2
3
4
0
1
0
]
A = begin{bmatrix} begin{matrix} 2 & 1 & 5\2 & 3 & 4\0 & 1 & 0\end{matrix} end{bmatrix}
A=⎣⎡220131540⎦⎤
对应的迹：
t
r
(
A
)
=
A
11
+
A
22
+
A
33
=
2
+
3
+
0
=
5
trleft( A right) = A_{11} + A_{22} + A_{33} = 2 + 3 + 0 = 5
tr(A)=A11+A22+A33=2+3+0=5
1.2 性质
t
r
(
A
+
B
)
=
t
r
(
A
)
+
t
r
(
B
)
trleft( {A + B} right) = trleft( A right) + trleft( B right)
tr(A+B)=tr(A)+tr(B)
t
r
(
a
A
)
=
a
⋅
t
r
(
A
)
trleft( {aA} right) = a cdot trleft( A right)
tr(aA)=a⋅tr(A)
t
r
(
α
A
+
β
B
)
=
α
⋅
t
r
(
A
)
+
β
⋅
t
r
(
B
)
trleft( {alpha A + beta B} right) = alpha cdot trleft( A right) + beta cdot trleft( B right)
tr(αA+βB)=α⋅tr(A)+β⋅tr(B)
t
r
(
A
T
)
=
t
r
(
A
)
trleft( {A^T } right) = trleft( A right)
tr(AT)=tr(A)
t
r
(
A
B
)
=
t
r
(
B
A
)
trleft( {AB} right) = trleft( {BA} right)
tr(AB)=tr(BA)
A
B
=
t
r
(
A
B
)
=
t
r
(
B
A
)
AB = trleft( {AB} right) = trleft( {BA} right)
AB=tr(AB)=tr(BA)
1.3 相关函数
1.3.1 调用函数形式
1
2
3
4
5
6
7import sys,os,math,time import matplotlib.pyplot as plt from numpy import * A = array([[1,2,3],[4,5,6],[7,8,9]]) print("trace(A): {}n".format(trace(A)))
1
2trace(A): 15
1.3.2 利用迹计算两个矩阵的内积
1
2
3
4
5
6
7
8
9
10
11import sys,os,math,time import matplotlib.pyplot as plt from numpy import * A = random.randn(15,8) B = random.randn(15,8) C = A.T.dot(B) print("trace(C): {}n".format(trace(C))) print("sum(A*B): {}n".format(sum(A*B)))
1
2
3trace(C): -9.301644996885578 sum(A*B): -9.301644996885576
§02 QR分解
2.1 定义
对于矩阵 A，可以将其表示成： A = Q ⋅ R A = Q cdot R A=Q⋅R 。其中 Q Q Q 是正交矩阵， R R R 是上三角矩阵。
2.2 分解举例
分解一个5×3随机矩阵。
1
2
3
4
5
6
7
8
9import sys,os,math,time import matplotlib.pyplot as plt from numpy import * A = random.randn(5,3) print("A: {}n".format(A)) q,r = linalg.qr(A) print("q: {}n".format(q),"r: {}n".format(r))
1
2
3
4
5
6
7
8
9
10
11
12
13
14A: [[-1.86374906 -1.14492839 0.25085956] [ 0.84097176 0.47786409 0.63319386] [-1.2215861 -0.84129822 -0.68549399] [ 0.14952506 -1.41793941 -0.28392431] [-0.7815916 -1.56835016 -0.23617405]] q: [[-0.74216383 0.11278664 0.58823716] [ 0.33488351 -0.07192668 0.58284231] [-0.48644801 0.02461369 -0.55319958] [ 0.0595424 -0.8284496 -0.04030384] [-0.31123773 -0.54329656 0.08134932]] r: [[2.51123671 1.82270331 0.41592522] [0. 1.84255932 0.32940707] [0. 0. 0.88806271]]
可以验证 q 矩阵是正交矩阵：
1
2print("q.T.dot(q): {}n".format(q.T.dot(q)))
1
2
3
4q.T.dot(q): [[1.00000000e+00 3.84861072e-17 2.96333633e-16] [3.84861072e-17 1.00000000e+00 8.91050746e-17] [2.96333633e-16 8.91050746e-17 1.00000000e+00]]
§03 特殊矩阵
3.1 空矩阵
1
2
3n = empty((5,5)) print("n: {}n".format(n))
1
2
3
4
5
6
7
8
9
10
11n: [[3.42247464e-316 3.42249708e-316 3.42250182e-316 3.06800300e-316 3.42251605e-316] [3.42252079e-316 3.42252553e-316 3.42253028e-316 3.42253502e-316 3.06797454e-316] [3.42253976e-316 3.42254925e-316 3.42250656e-316 3.42251130e-316 3.42248759e-316] [3.06797928e-316 3.06800774e-316 3.06799351e-316 3.06798403e-316 3.06798877e-316] [3.06794608e-316 3.06796505e-316 3.06796980e-316 3.42254451e-316 1.04878799e+248]]
3.2 零矩阵
1
2
3n = zeros((5,5)) print("n: {}n".format(n))
1
2
3
4
5
6n: [[0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.] [0. 0. 0. 0. 0.]]
3.3 1矩阵
1
2
3n = ones((5,5)) print("n: {}n".format(n))
1
2
3
4
5
6n: [[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
3.4 对角线矩阵
1
2
3n = eye(3,4,0) print("n:n{}".format(n))
1
2
3
4
5n: [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.]]
1
2
3n = eye(3,4,1) print("n:n{}".format(n))
1
2
3
4
5n: [[0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
1
2
3n = eye(3,4,-1) print("n:n{}".format(n))
1
2
3n = diag([1,2,3,4]) print("n:n{}".format(n))
1
2
3
4
5
6n: [[1 0 0 0] [0 2 0 0] [0 0 3 0] [0 0 0 4]]
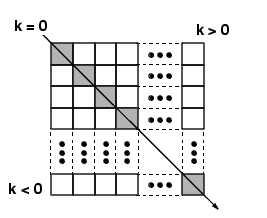
▲ 图3.4.1 Matrix Diagnoal
3.5 随机矩阵
1
2
3n = random.random((5,4)) print("n:n{}".format(n))
1
2
3
4
5
6
7n: [[0.01356284 0.90473283 0.97940574 0.28104009] [0.47466198 0.27617192 0.74221122 0.20462867] [0.34521728 0.46786105 0.24819072 0.71578562] [0.51775933 0.51530835 0.06254809 0.92659839] [0.30551515 0.60956763 0.43818475 0.31937707]]
■ 相关文献链接:
- Trace of a matrix
● 相关图表链接:
- 图3.4.1 Matrix Diagnoal
最后
以上就是可耐雪糕最近收集整理的关于numpy中计算矩阵数值的核心函数 §01 矩阵的迹 §02 QR分解 §03 特殊矩阵 的全部内容，更多相关numpy中计算矩阵数值的核心函数 内容请搜索靠谱客的其他文章。
发表评论 取消回复