其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》,清华大学出版社,雷明著,由SIGAI公众号作者倾力打造。
- 书的购买链接
- 书的勘误,优化,源代码资源
原创声明:本文为 SIGAI 原创文章,仅供个人学习使用,未经允许,不能用于商业目的。
欢迎搜索关注微信公众号SIGAICN,获取更多原创干货

导言
支持向量机(SVM)在很多分类问题上曾经取得了当时最好的性能,使用非线性核的支持向量机可以处理线性不可分的问题。仅仅通过一个简单的核函数映射,就能达到如此好的效果,这让我们觉得有些不可思议。核函数过于抽象,在本文中,SIGAI将通过一组实验来演示核函数的有效性,并解释支持向量机各个参数所起到的作用,让大家对此有一个直观的认识。如果要了解SVM的理论,请阅读我们之前的公众号文章“用一张图理解SVM的脉络”。
核映射与核函数
通过核函数,支持向量机可以将特征向量映射到更高维的空间中,使得原本线性不可分的数据在映射之后的空间中变得线性可分。假设原始向量为x,映射之后的向量为z,这个映射为:
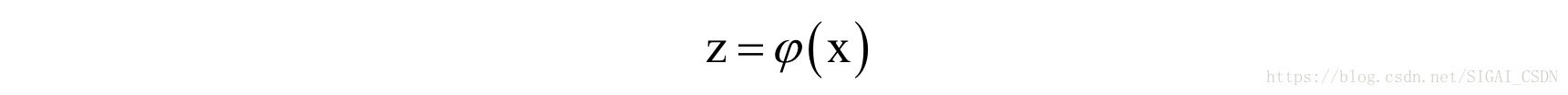
在实现时不需要直接对特征向量做这个映射,而是用核函数对两个特征向量的内积进行变换,这样做等价于先对向量进行映射然后再做内积:
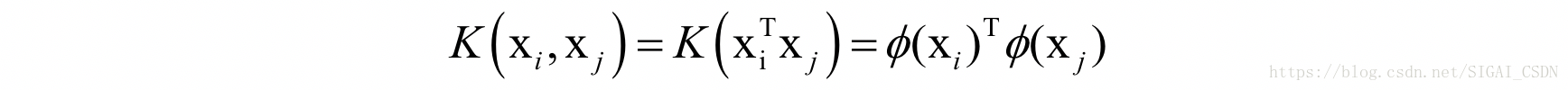
在这里K为核函数。常用的非线性核函数有多项式核,高斯核(也叫径向基函数核,RBF)。下表列出了各种核函数的计算公式:
各种核函数与它们的计算公式
| 核函数 | 计算公式 |
| 线性核 |
|
| 多项式核 |
|
| 径向基函数核/高斯核 |
|
| sigmoid核 |
|
其中![]() ,b,d为人工设置的参数,d是一个正整数,
,b,d为人工设置的参数,d是一个正整数,![]() 为正实数,b为非负实数。
为正实数,b为非负实数。
使用核函数后,支持向量机在训练时求解的对偶问题为:
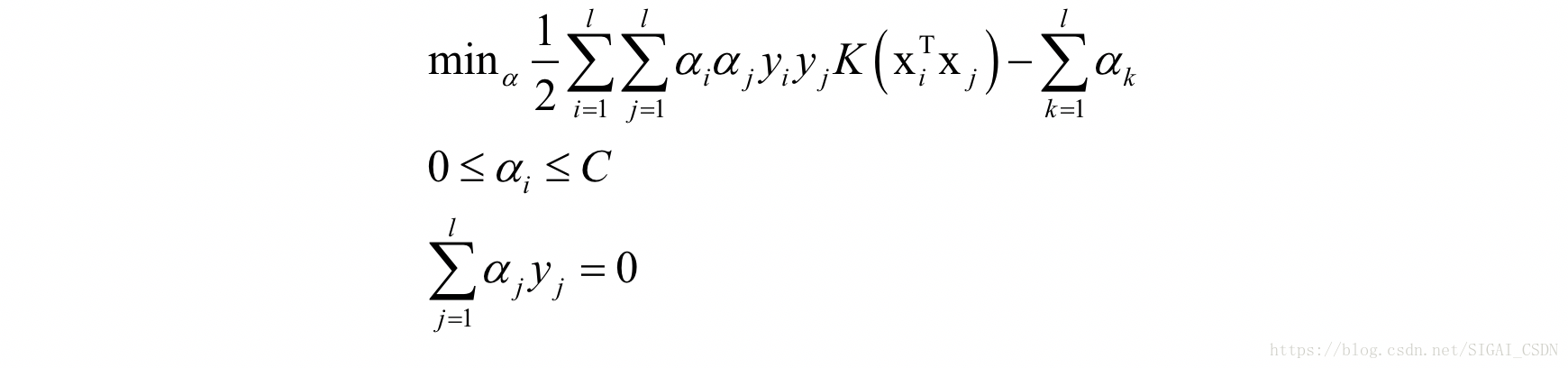

其中sgn为符号函数,定义为:
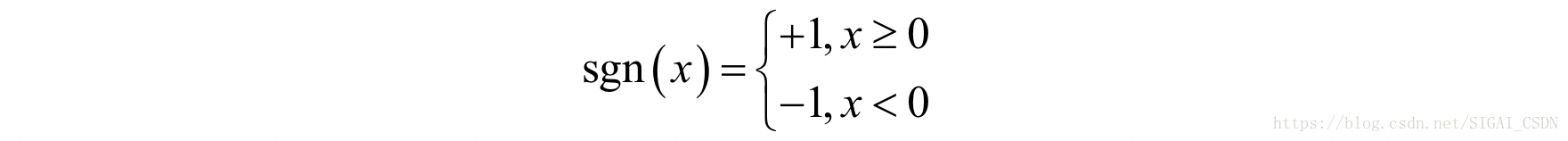
实验
支持向量机真的能对非线性的数据进行分类吗?不同的训练参数会对分类结果产生什么样的影响?下面我们用一个小实验来验证。在这里,我们对二维平面上512x512像素的图像中的所有点进行分类,有蓝色和红色两类。先用一批样本训练一个模型,然后对平面内所有的点进行分类,分类结果的颜色和训练样本的颜色相同。
首先来看支持向量机能否处理异或问题,这是人工智能里一个很经典的分类问题,两类训练样本分别落在两个对角线上:
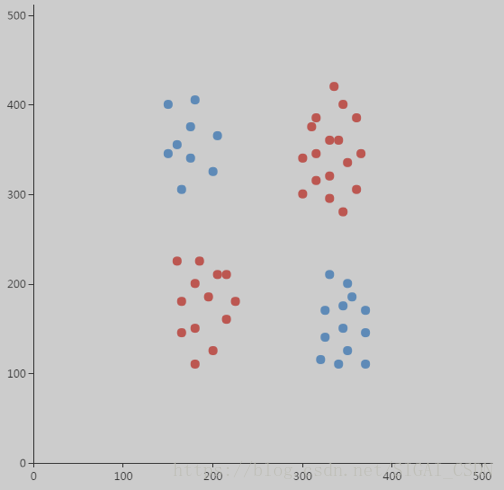
显然,用一条直线无论怎样划分都无法将这两类样本正确的分开。下面来看SVM的表现,我们使用线性核,多项式核,高斯核三种核函数进行训练。
首先选用线性核,结果是这样的:
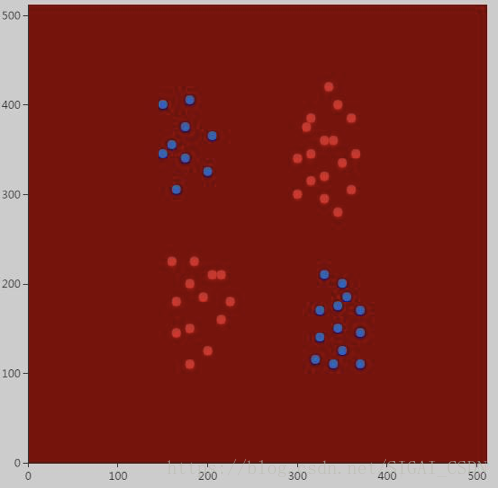
所有样本都被判定成红色。不出所料,使用线性核的SVM是无法解决异或问题的。
接下来选用多项式核。首先将参数设置为:

分类效果非常差:
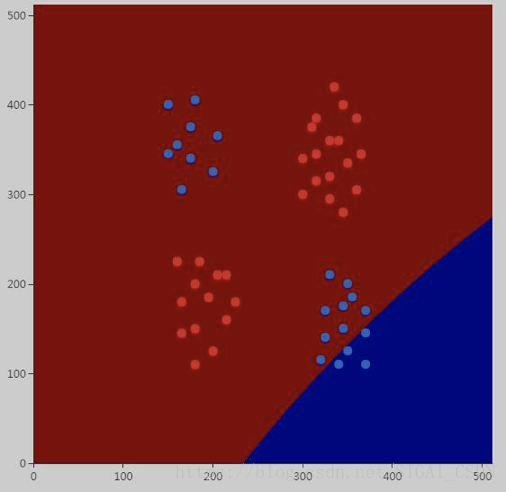
蓝色的样本只有少数被分对了。下面调整训练参数:

这里只加大了惩罚因子C的子,分类效果如下:
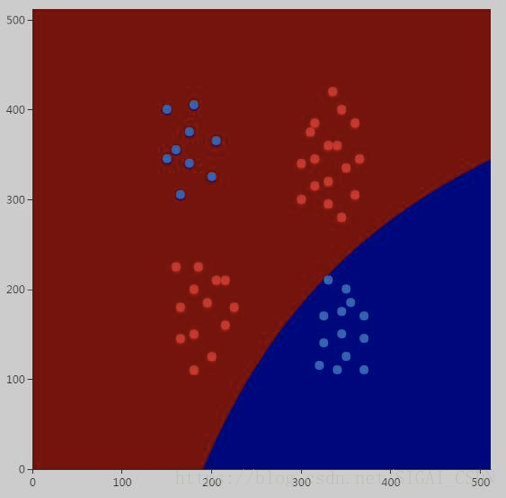
这比之前好了,蓝色的样本有一半被分对。接着调整参数:

分类效果如下:
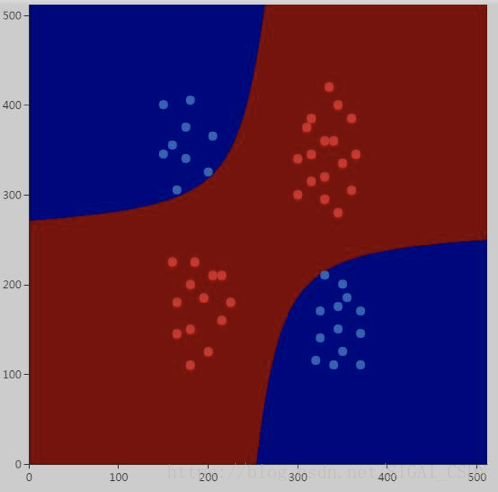
现在是见证奇迹的时刻!所有训练样本都被正确分类,看来加大C的值非常有效。
下面来看高斯核的表现,如果参数设置为:

分类效果也是非常差:
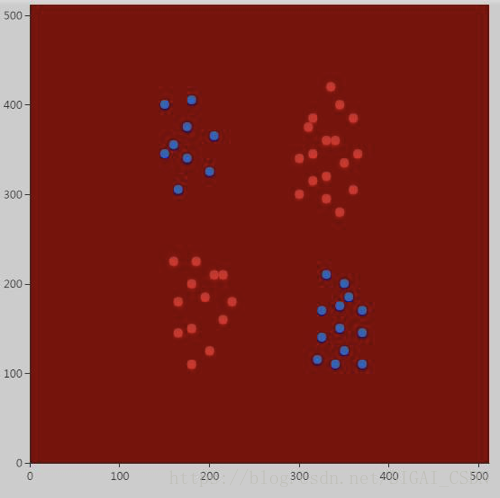
所有的点都被分成了红色。下面加大惩罚因子的值:

大部分训练样本都可以正确分类:
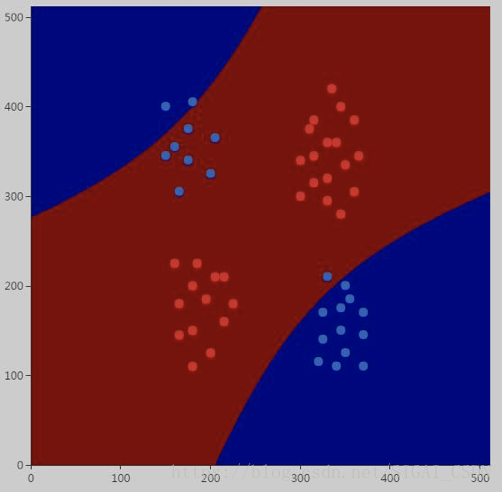
进一步加大C的值:

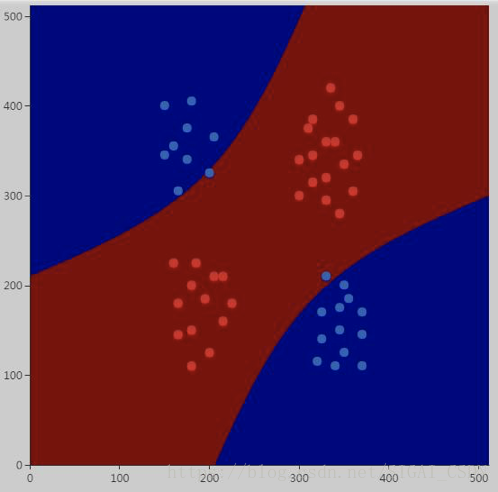
效果比刚才更好,所有样本基本上都被正确分类了。
继续调整,加大C的值:

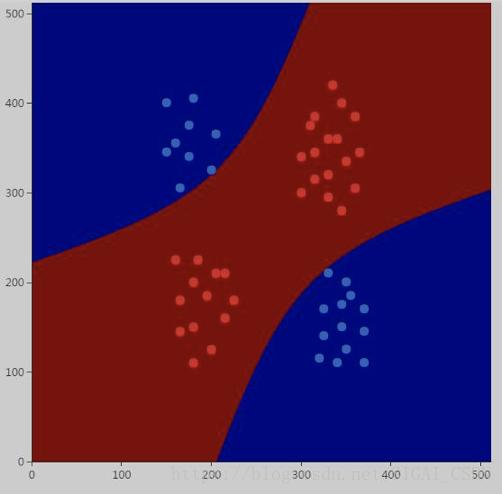
所有样本都被正确分类。
如果我们只加大![]() 的值,也能达到很好的效果:
的值,也能达到很好的效果:

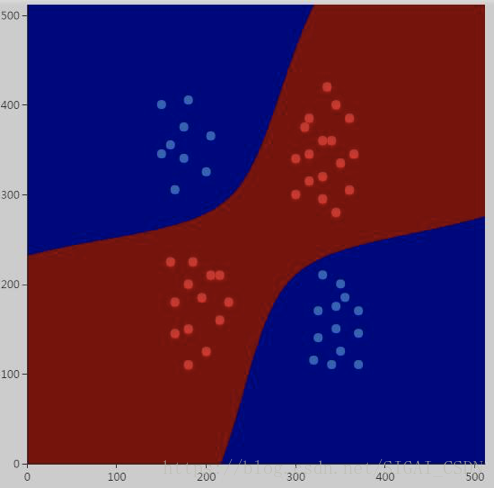
所有样本同样被正确分类。
结论
通过上面的实验我们发现使用多项式核、高斯核的SVM确实是可以解决线性不可分问题的。不同的参数对精度的影响非常大,一般来说,C越大,训练得到的模型越准确。如果采用高斯核,参数![]() 的值对精度影响也非常大。因此,在实际应用时调一组好的参数对使用效果非常重要!
的值对精度影响也非常大。因此,在实际应用时调一组好的参数对使用效果非常重要!
推荐文章
[1] 机器学习-波澜壮阔40年 SIGAI 2018.4.13.
[2] 学好机器学习需要哪些数学知识?SIGAI 2018.4.17.
[3] 人脸识别算法演化史 SIGAI 2018.4.20.
[4] 基于深度学习的目标检测算法综述 SIGAI 2018.4.24.
[5] 卷积神经网络为什么能够称霸计算机视觉领域? SIGAI 2018.4.26.
[6] 用一张图理解SVM的脉络 SIGAI 2018.4.28.
[7] 人脸检测算法综述 SIGAI 2018.5.3.
[8] 理解神经网络的激活函数 SIGAI 2018.5.5.
[9] 深度卷积神经网络演化历史及结构改进脉络-40页长文全面解读 SIGAI 2018.5.8.
[10] 理解梯度下降法 SIGAI 2018.5.11.
[11] 循环神经网络综述—语音识别与自然语言处理的利器 SIGAI 2018.5.15
[12] 理解凸优化 SIGAI 2018.5.18.
原创声明
本文为 SIGAI 原创文章,仅供个人学习使用,未经允许,不能用于商业目的。

最后
以上就是感动电源最近收集整理的关于用实验理解SVM的核函数和参数的全部内容,更多相关用实验理解SVM内容请搜索靠谱客的其他文章。








发表评论 取消回复