Picture
Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2435 Accepted Submission(s): 1294
Problem Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.
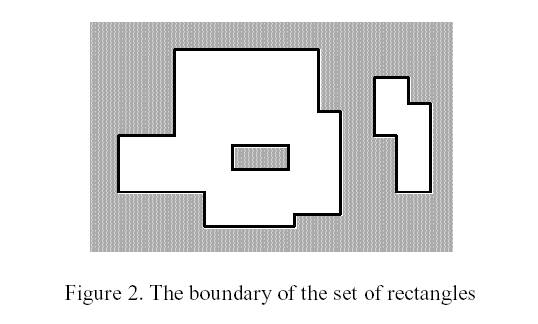
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
周长并和面积并一样是扫描线法,从下到上扫过去,用len表示当前区间线段长度,那么每次扫描的时候要加上当前的len[1]减去上次的len[1]的绝对值(因为上次的len已经加过了),这是水平方向的。还有竖直方向,用segnum数组维护当前区间的线段共能在竖直方向构成多少条线段(其实就是有当前区间的线段有多少个端点),维护segnum数组还需要两个bool数组lb,rb分别表示当前区间的左端点和右端点是否被线段覆盖,那么segnum[o]=segnum[o<<1]+segnum[o<<1|1],若rb[o<<1]&&lb[o<<1|1],说明两条线段重合了,segnum[o]要减2。
别忘了最后一条边,因为扫描完倒数第二条边后len[1]的长度就是最后一条边的长度,所以最后还要加上len[1]。
因为这道题坐标范围不大,所以可以用线段树表示坐标,也可以像面积并那样先把所有x记下来从小到大排序,每次更新的时候先二分找到坐标的编号,线段树表示的不是真实坐标,而是x的相对坐标,相当于离散化一下。
两种方法的代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdlib>
#define INF 0x3f3f3f3f
#define MAXN 10010
#define MAXM 20010
#define MAXNODE 4*MAXN
using namespace std;
int N,M,covered[MAXM<<2],segnum[MAXM<<2],len[MAXM<<2];
bool lb[MAXM<<2],rb[MAXM<<2];
struct Line{
int x1,x2,y,cover;
bool operator < (const Line& x) const{
return y<x.y;
}
}line[MAXN];
void add_line(int x1,int y1,int x2,int y2){
line[M].x1=x1;
line[M].x2=x2;
line[M].y=y1;
line[M++].cover=1;
line[M].x1=x1;
line[M].x2=x2;
line[M].y=y2;
line[M++].cover=-1;
}
void maintain(int o,int L,int R){
if(covered[o]){
lb[o]=rb[o]=1;
len[o]=R-L;
segnum[o]=2;
}
else if(L+1>=R) lb[o]=rb[o]=len[o]=segnum[o]=0;
else{
lb[o]=lb[o<<1];
rb[o]=rb[o<<1|1];
len[o]=len[o<<1]+len[o<<1|1];
segnum[o]=segnum[o<<1]+segnum[o<<1|1];
if(rb[o<<1]&&lb[o<<1|1]) segnum[o]-=2;
}
}
void update(int o,int L,int R,int ql,int qr,int cover){
if(ql<=L&&qr>=R){
covered[o]+=cover;
maintain(o,L,R);
return;
}
int mid=(L+R)>>1;
if(ql<mid) update(o<<1,L,mid,ql,qr,cover);
if(qr>mid) update(o<<1|1,mid,R,ql,qr,cover);
maintain(o,L,R);
}
int main(){
freopen("in.txt","r",stdin);
while(scanf("%d",&N)!=EOF){
M=0;
int LB=INF,RB=-INF;
while(N--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
LB=min(LB,x1);
RB=max(RB,x2);
add_line(x1,y1,x2,y2);
}
sort(line,line+M);
for(int i=0;i<(MAXM<<2);i++) lb[i]=rb[i]=covered[i]=segnum[i]=len[i]=0;
int last=0,ans=0;
for(int i=0;i<M-1;i++){
update(1,LB,RB,line[i].x1,line[i].x2,line[i].cover);
ans+=segnum[1]*(line[i+1].y-line[i].y);
ans+=abs(len[1]-last);
last=len[1];
}
ans+=len[1];
printf("%dn",ans);
}
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdlib>
#define INF 0x3f3f3f3f
#define MAXN 10010
#define MAXM 10010
#define MAXNODE 4*MAXN
using namespace std;
int N,M,covered[MAXM<<2],segnum[MAXM<<2],len[MAXM<<2],x[MAXN<<1];
bool lb[MAXM<<2],rb[MAXM<<2];
struct Line{
int x1,x2,y,cover;
bool operator < (const Line& x) const{
return y<x.y;
}
}line[MAXN];
void add_line(int x1,int y1,int x2,int y2){
line[M].x1=x1;
line[M].x2=x2;
line[M].y=y1;
line[M++].cover=1;
line[M].x1=x1;
line[M].x2=x2;
line[M].y=y2;
line[M++].cover=-1;
}
void maintain(int o,int L,int R){
if(covered[o]){
lb[o]=rb[o]=1;
len[o]=x[R]-x[L];
segnum[o]=2;
}
else if(L+1>=R) lb[o]=rb[o]=len[o]=segnum[o]=0;
else{
lb[o]=lb[o<<1];
rb[o]=rb[o<<1|1];
len[o]=len[o<<1]+len[o<<1|1];
segnum[o]=segnum[o<<1]+segnum[o<<1|1];
if(rb[o<<1]&&lb[o<<1|1]) segnum[o]-=2;
}
}
void update(int o,int L,int R,int ql,int qr,int cover){
if(ql<=L&&qr>=R){
covered[o]+=cover;
maintain(o,L,R);
return;
}
int mid=(L+R)>>1;
if(ql<mid) update(o<<1,L,mid,ql,qr,cover);
if(qr>mid) update(o<<1|1,mid,R,ql,qr,cover);
maintain(o,L,R);
}
int main(){
freopen("in.txt","r",stdin);
while(scanf("%d",&N)!=EOF){
M=0;
int NX=1;
while(N--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
x[NX++]=x1;
x[NX++]=x2;
add_line(x1,y1,x2,y2);
}
sort(x+1,x+NX);
sort(line,line+M);
NX=unique(x+1,x+NX)-x-1;
for(int i=0;i<(MAXM<<2);i++) lb[i]=rb[i]=covered[i]=segnum[i]=len[i]=0;
int last=0,ans=0;
for(int i=0;i<M-1;i++){
int l=lower_bound(x+1,x+NX,line[i].x1)-x,r=lower_bound(x+1,x+NX,line[i].x2)-x;
update(1,1,NX,l,r,line[i].cover);
ans+=segnum[1]*(line[i+1].y-line[i].y);
ans+=abs(len[1]-last);
last=len[1];
}
ans+=len[1];
printf("%dn",ans);
}
return 0;
}
最后
以上就是成就铃铛最近收集整理的关于hdu1828 矩形周长并Picture 的全部内容,更多相关hdu1828内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。









发表评论 取消回复