比赛经验总结--187

cqround1

1.这次比赛160分

(1)反质数：60

(2)二分答案+2sat：验证:  0分

(3)树上LCA+推公式: 100分

2.总结：这次比赛第三题做起来非常顺，做过类似的题:奶牛大集会nkoj3689，树上的lca加乱搞基本上就是这样，注意画一些复杂的图(儿子祖先画全)不要凭空想，因为这种式子很容易推错，这里差一点那里差一点就爆0了。第一题，虽然反质数并没有学过，但是其实仔细想一想是推得出来的，关于反质数，可以看这篇解题报告点击打开链接。第二题超纲，但是看懂了还是感觉很厉害，那么通常什么情况可以使用2sat?对于每一个东西，有两种情况并且必须二选一！

cqround2

1.这次比赛300分

(1)乱搞模拟:100

(2)打铁:100

(3)倒序+并查集：100

2.总结:这次虽说ak了，可以说是运气好吧。当然也是一中的题确实水分比较重，感觉到处找了几道题，有先天优势，第二题做过两次的原题，当年也是自己推出来的。第一题难点在于读题难！这个题也可以提示关于输入:example:255.255.255.247   。怎么读这四个数呢？(1).输入优化直接无视'.'(2)scanf("%d.%d.%d.%d",...)。第三题有人剧透了是并查集，那就是并查集撒。这个题，注意到并查集仅支持合并操作，但此题题意的意思是要断开，正起断开，那么就倒起来合并！这种思想的题是做过的：假期关楼。先把他不断的边连接的节点用并查集合并，与1联通的节点就是掉不下去的。倒序讨论断开的边，合并，在什么时候与1联通，这一块所含节点的ans就是段边的时间。加油！！！

cqround3

1.这次比赛145分！亏的一匹

(1)找规律+组合数取模:25

(2)trie+dp:100

(3)构造序列：20

2.总结：惨！第一题死因：1e9+7打成了1000000009！！！第二题比较好想的dp，对于每一个位置，很显然要找出为当前1--i这个字符串后缀的单词，字典树！第三题确实厉害，难想，看懂了觉得神题一道。

cqround4

1.这次比赛200分

(1)暴力打出来找规律!

(2)观察代码,很简单的gcd

(3)堆+贪心

2.总结：仔细审题!!!第一题最开始没看到(n-1)是(m-1)的倍数,打表找不出规律。第三题确实比较厉害，但是有一个经典的贪心原则，详情见nkoj3827

西南联训6

1.这次比赛200分

(1)dfs，类似重庆排位赛1反质数！

(2)区间dp

(3)图论

2.总结：仔细审题!!!第一题最开始没看到(n-1)是(m-1)的倍数,打表找不出规律。第三题确实比较厉害，但是有一个经典的贪心原则，详情见nkoj3827

cqround5

1.这次比赛190分

(1)分析找通式

(2)树形dp（打铁）

(3)国家队训练题，90分算法（暴力spfa10分+树上lca30分+mst树上lca多一条边单独算50分）

2.总结：第一题不说了，仔细分析还是比较容易，但是尽量少用点时间，这几场第一题都用了一个小时多一点。第二题一道树形dp（打铁），当时确实没做出来，状态定的不对，树形dp要复习一下！第三题能拿到得分都拿到了，拿到题先看看数据范围，10分暴力送分，30分lca（m==n-1），50分mst+lca+单独一条边单独算。正解思路大概懂了，但是目前还是写不出代码。。。

cqround6

1.这次比赛190（200）分（一中第二题数据有一组不合法）

(1)分析找规律

(2)图论dijkstra+top打铁

(3)dfs

2.总结：第一题还是比较容易，对于当前选了一些硬币的和为sum，那么下一枚硬币的面值p必须在1---sum+1之间，这样才能满足选了这枚硬币后，1----sum+p之间的值全部能凑出来，这个是在草稿本上用了10分钟推出来的。那么怎么保证所选硬币个数最少呢？因为p必须在1---sum+1之间，当然取区间中面值最大的，一定是最优的。其实仅仅就是这样很容易卡，比如1e9 2 1 2这样的数据不管是循环还是递归都会死掉，后面又想出来了这个东西。当sum>=p[n]即和不小于最大面值的硬币的时候，根据前面提到的原则肯定就选p[n]!这个时候就不需要再去模拟了，直接除就行了，这个是肯定卡不掉的。一中数据太辣鸡，导致写暴力的人都a了。第二题大水题，反向最短路+top打铁。第三题dfs，dfs再一次的死了，搜索能力还需加强！关于这个题，最开始是写的搜完了再check，但是发现边搜边check效率高到爆炸，详情参见nkoj3849游戏！

10.31的一个智障错！

新oj真的良心，爆0的代码拿了95分。三分法的下界没赋初值！能拿多少分全凭运气！记住非全局变量记得赋初值

11.3模拟赛

1.这次比赛170分

(1)暴力送分题100

(2)正解：双hash，送的50分拿好。

(3)正解dp，dfs30分剪枝剪成了20分

2.总结：先说第二题，本来考试的时候想到了hash，并且在考虑一个子串---->下一个子串时，如何在O(1)的复杂度内处理出下一个子串的hash。但是，hash学的撇！不知道hash可以直接这么搞！

以今天第二题为例：好文章

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<stack>
#define ull unsigned long long
#define puu pair<ull,ull>
#define mp make_pair
using namespace std;
const ull seed1=31;
const ull seed2=131;
const ull mod1=1875647;
const ull mod2=3838437;
inline void _read(int &x){
    char t=getchar();bool sign=true;
    while(t<'0'||t>'9')
    {if(t=='-')sign=false;t=getchar();}
    for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
    if(!sign)x=-x;
}
ull temp1=1,temp2=1;
ull hash1,hash2;
int n,m;
char s[200005];
puu ans[200005];
ull tot=0;
int main(){
	int i,j,k;
	cin>>n>>m;
	scanf("%s",s+1);
	for(i=1;i<=m;i++){
		hash1=(hash1*seed1+s[i])%mod1;
		hash2=(hash2*seed2+s[i])%mod2;
		temp1=temp1*seed1%mod1;
		temp2=temp2*seed2%mod2;
	}
	ans[++tot]=mp(hash1,hash2);
	for(i=m+1;i<=n;i++){
		hash1=(hash1*seed1%mod1+s[i]+mod1-temp1*s[i-m]%mod1)%mod1;
		hash2=(hash2*seed2%mod2+s[i]+mod2-temp2*s[i-m]%mod2)%mod2;
		ans[++tot]=mp(hash1,hash2);
	}
	sort(ans+1,ans+1+tot);
	tot=unique(ans+1,ans+1+tot)-ans-1;
	cout<<tot;
}

原型BKDRhash。O(1)转移出下一个长度为m的子串的hash，hash每处理一个新的元素乘一次seed，因为子串长度为m，一个元素从进入这个hash到离开，乘了m次seed，减去即可！注意不要乱取模，hash是一门玄学，可以记住这个写法！

下面说说第三题：好线路

考试的时候推出了这一个很关键的式子：要求的:方差*(n+m-1)^2，令n-m+1=k,可化简为：k*(x1^2+x2^2+..+xk^2)-(x1+x2+..xk)^2。然而想出了这个式子却还是想着dfs！！！想dp的时候却想的是方差的定义式，有后效性。dp该从我推出的这个式子入手！想一想把xk这个项分离出来跟前面的x1....xk-1产生关系。于是得到：k*(x1^2+x2^2+...xt^2)-(x1+x2+...xt)^2 = k*(x1^2+x2^2+...+xt-1^2)-(x1+x2+...+xt-1)^2+k*xt^2  -xt^2 - 2*(x1+x2+...+xt-1)*xt =  k*(x1^2+x2^2+...+xt-1^2)-(x1+x2+...+xt-1)^2 +(k-1)*xt^2 -2*(x1+x2+...+xt-1)*xt

递推关系出来了，dp！

f[i][j][s]:当前的到第i行第j列，并且当前路径上的权值和为s，这个式子k*(x1^2+x2^2+...xt^2)-(x1+x2+...xt)^2的最小值。

由之前推出的式子:

f[i][j][s]=min ( f[i][j-1][s-map[i][j]] , f[i-1][j][s-map[i][j]] ) + (k-1) * ( map[i][j] ) ^ 2  -  2 * ( s - map[i][j] ) * map[i][j]

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
const int inf=0x3f3f3f3f;
inline void _read(int &x){
    char t=getchar();bool sign=true;
    while(t<'0'||t>'9')
    {if(t=='-')sign=false;t=getchar();}
    for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
    if(!sign)x=-x;
}
int n,m,k;
int ans=inf;
int map[55][55];
int f[55][55][5000];
int minn[55][55];
int maxn[55][55];
int lim;
int main(){
	int i,j,h,s;
	cin>>n>>m;
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			cin>>map[i][j];
		}
	}
	k=n+m-1;
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			minn[i][j]=min(minn[i-1][j],minn[i][j-1])+map[i][j];
			maxn[i][j]=max(maxn[i-1][j],maxn[i][j-1])+map[i][j];
		}
	}
	lim=maxn[n][m];
	//f[1][1][map[1][1]]=(k-1)*map[1][1]*map[1][1];
	for(i=0;i<=n;i++){
		for(j=0;j<=m;j++){
        	for(s=0;s<=lim;s++){
            	f[i][j][s]=inf;
        	}
    	}
    }
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			if(i==1&&j==1){
				f[i][j][map[1][1]]=(k-1)*map[1][1]*map[1][1];
				continue;
			}
			for(s=minn[i][j];s<=maxn[i][j];s++){
				f[i][j][s]=min(f[i-1][j][s-map[i][j]],f[i][j-1][s-map[i][j]])+(k-1)*map[i][j]*map[i][j]-2*(s-map[i][j])*map[i][j];
			}
		}
	}
	for(i=minn[n][m];i<=maxn[n][m];i++){
		ans=min(ans,f[n][m][i]);
	}
	cout<<ans;
}

cqround8

1.这次比赛170，最垃圾的一次

(1)dp100分

(2)单调队列(栈)，类似于广告牌模型

(3)类似gcd递归解决

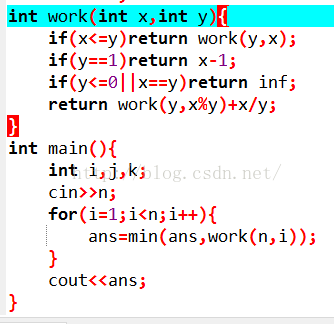
2.总结：这次比赛值得好还反省！有史以来最丑的一次！第一题稍微提一下，注意到贪心是有问题的！第二题，思维方向有问题，我想的是先枚举点，再看包含这个点的子矩阵。而实际上对于这种题，应该先枚举矩阵，再来看其中的最小值是什么！比如今天这个题，应该枚举第i排到第j排再看区间中的最小值，min[k]表示第k列中，第i排到第j排的最小值，对于第i排到第j排之间，要让min[k]是子矩阵中的最小值，考虑k往两边延展，例如往左找到第一个小于min[k]的min[h]，那么记left[k]=h+1，即k往左最多可以延展到h，往右同理，记right[k]，那么right，left怎么处理，往左第一个比自己小的：单调队列！那么对于第i排到第j排中，以min[k]为最小值的子矩阵个数很显然就是(right[k]-k+1)*(k-left[k]+1)。说说第三题，正难则反！倒过来思考，状态(a,b)令(a>=b)可以转移至(a+k*b,b),那么倒过来也就很简单了，用类似于gcd的方式倒过来计算，work(x,y)表示到状态(x,y)所需的步数(令x>=y)。而题目要求至少一个为n，那么就取work(n,i)的最小值即可。

对拍模板

@echo off
:loop
makedata.exe
baoli.exe
zhengjie.exe
fc baoli.out ans.out
if not errorlevel 1 goto loop
pause
:end

最后

以上就是怡然老虎为你收集整理的比赛经验总结--187的全部内容，希望文章能够帮你解决比赛经验总结--187所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。