HDU-1166 敌兵布阵（树状数组详解）

树状数组和线段树的区别：

树状数组可以解决的问题都可以用线段树解决，这两者的区别在于树状数组的系数要少很多，就比如字符串模拟大数可以解决大数问题，也可以解决1+1的问题，但没人会在1+1的问题上用大数模拟。

树状数组的优点和缺点：
树状数组的优点是修改和查询的复杂度都是O(logN)，而且相比线段树系数要少很多，比传统数组要快，而且容易写。
缺点是遇到复杂的区间问题还是不能解决，功能还是有限。

树状数组的介绍：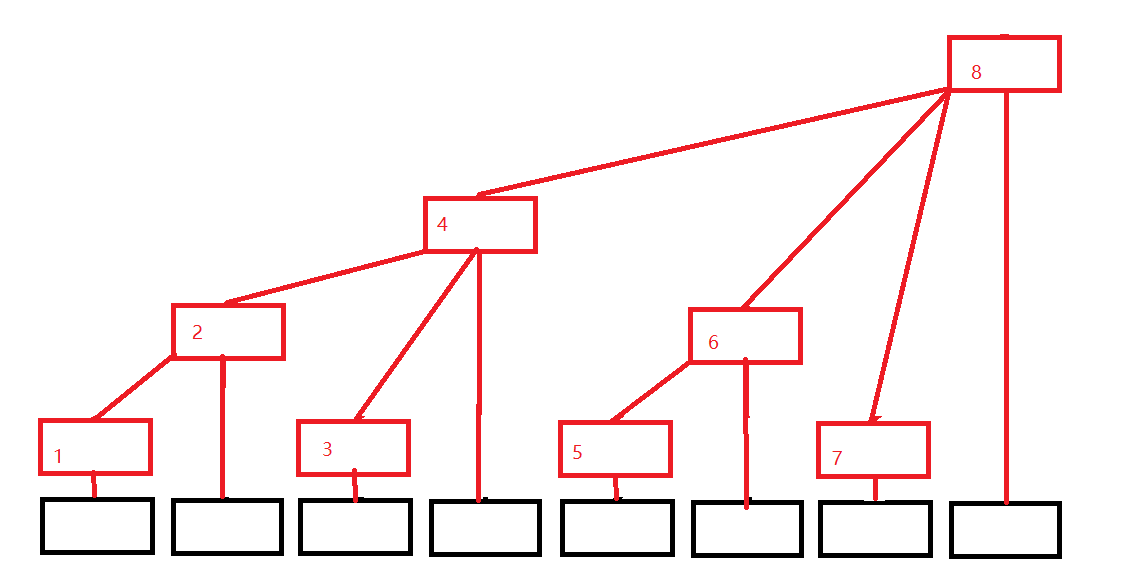

Tree[1] = A[1];
Tree[2] = A[1] + A[2];
Tree[3] = A[3];
Tree[4] = A[1] + A[2] + A[3] + A[4];
Tree[5] = A[5];
Tree[6] = A[5] + A[6];
Tree[7] = A[7];
Tree[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

可以发现,这颗树是有规律的

Tree[i] = A[i - 2^k +1] + A[i - 2 ^ k+2] + … + A[i]; //k为i的二进制中从最低位到高位连续零的长度
例如8的二进制为1000，因此k为3，Tree[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]

如果要实现求和，例如求前7项的和，SUM(7)=Tree[7]+Tree[6]+Tree[4]
可以得到SUMi = Tree[i] + Tree[i-2k1] + Tree[(i - 2k1) - 2k2] + …；
而2^k=(i)&(-i),通常叫做lowbit函数

int lowbit(int x)
{
    return x&(-x);
}

lowbit(x)是x的二进制表达式中最低位的1所对应的值。

比如，6的二进制是110，所以lowbit(6)=2。

此时，就可以来构造树状数组

区间更新：

void update(int i,int k)//在i位置加上k
{
	while(i<=n)
	{
		tree[i]+=k;
		i+=lowbit(i);
	}
}

求和：

int getsum(int i)//求A[1 - i]的和
{
	int sum=0;
	while(i>0)
	{
		sum+=tree[i];
		i-=lowbit(i);
	}
	return sum;
}

下面是一道树状数组模板题
敌兵布阵

代码：

#include <iostream>
using namespace std;
#include <cstring> 

int n,m;
int a[50005],tree[50005];//原数组和树状数组 

int lowbit(int x)
{
	return x&(-x);
} 

void update(int i,int k)//在i位置加上k
{
	while(i<=n)
	{
		tree[i]+=k;
		i+=lowbit(i);
	}
}

int getsum(int i)//求A[1 - i]的和
{
	int sum=0;
	while(i>0)
	{
		sum+=tree[i];
		i-=lowbit(i);
	}
	return sum;
}

int main()
{
	int t;
	cin>>t;
	int s=1;
	while(t--)
	{
		cout<<"Case "<<s<<":"<<endl;
		s++;
		memset(a,0,sizeof(a));
		memset(tree,0,sizeof(tree));
		cin>>n;
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
			update(i,a[i]);//输入初值的时候，也相当于更新了值
		}
		
		string s;
		int a,b;
        while(cin>>s&&s!="End")
		{
             cin>>a>>b;
             if(s=="Query")//求和操作
			 {    
                 int sum = getsum(b) - getsum(a-1);    //a-b区间和也就等于1-b区间和减去1-(a-1)区间和
                 cout << sum << endl;
             }
             else if(s=="Add")//加法 
			 {
                update(a,b);
             }
             else if(s=="Sub")
			 {
                 update(a,-b);   //减法，即为加上相反数
             }
         }
 
 	}


	return 0;
}

最后

以上就是知性仙人掌为你收集整理的HDU-1166 敌兵布阵（树状数组详解）的全部内容，希望文章能够帮你解决HDU-1166 敌兵布阵（树状数组详解）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。