基本环境

documentclass[border=10pt]{standalone}
usepackage{pgfplots}
usepgfplotslibrary{polar,colormaps}	% polar: 极坐标， colormaps: 颜色
begin{document}
begin{tikzpicture}
  begin{polaraxis}[	% 极坐标申明
      domain  = -14400:14400,	% 区间
      samples = 5000,	% 数量
      colormap/cool,
      hide axis				% 坐标轴隐藏
    ]
    content
  end{polaraxis}
end{tikzpicture}
end{document}

原例

begin{polaraxis}[
	domain=-14400:14400,
	samples=3000,
	colormap/cool,
	hide axis
]
addplot[no markers, mesh, opacity=0.5]{1 - sin(x * 40 / 39)};
end{polaraxis}

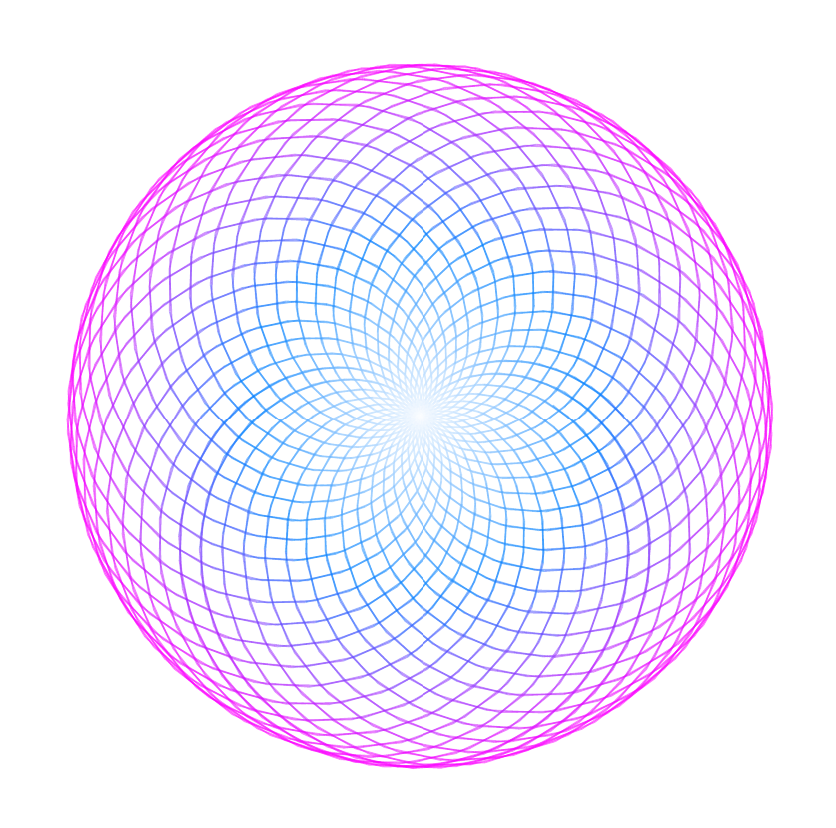
变体

$$f(x)=1-sin(x)$$

都是基于基础图像进行偏移

$$f(x)=1-sin(0.999x)$$

比例容易周期，就缝就特别大

$$f(x)=1-sin(0.99x)$$

单周期，多变化就很好看
$$f(x)=1-sin(0.99x)$$

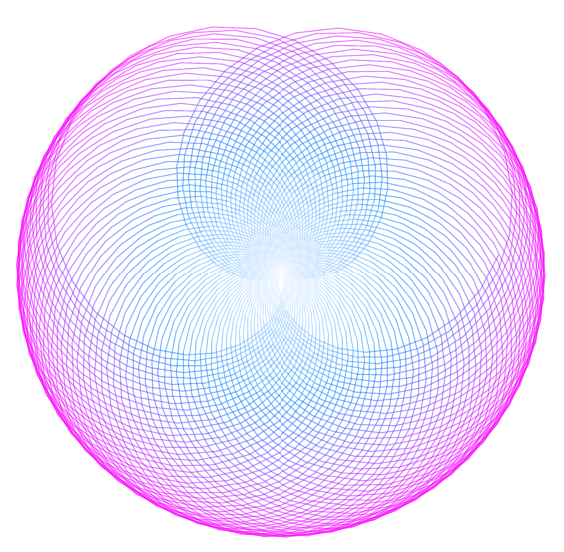
无周期

$$f(x)=1-sin(\pi x)$$

整数控制间隔，小数抖动描边

$$f(x)=1-sin(3.004x)$$

$$f(x)=1-sin(7.002x)$$

$$f(x)=1-sin(7.00009x)$$

描边越细，边缘越柔和

创建

documentclass[border=10pt]{standalone}
usepackage{pgfplots}
usepgfplotslibrary{polar,colormaps}
begin{document}
begin{tikzpicture}
  begin{polaraxis}[
      domain  = -14400:14400,
      samples = 3000,
      colormap/cool,
      hide axis
    ]
 addplot[no markers, mesh, opacity=0.5]{sin(x) *cos(x)};
  end{polaraxis}
end{tikzpicture}
end{document}

描边增粗

$$f(x)=sin(0.999x)cos(x)$$

$$f(x)=sin(x)cos(0.999x)$$

$$f(x)=sin(0.999x)cos(0.999x)$$

间隔分瓣

$$f(x)=sin(3x)cos(3x)$$

分瓣描边

$$f(x)=sin(1.999x)cos(1.999x)$$

$$f(x)=sin(7.3x)cos(3.3x)$$

形态变换

$$f(x)=sin(\pi x)cos(\pi x)$$

小数描边

中间太密集，转换一下

$$f(x)=1-sin(\pi x)cos(\pi x)$$

$$f(x)=1-sin(7.3x)cos(3.3x)$$

$$f(x)=1-sin(7.3x)cos(7.3x)$$

最后

以上就是含蓄蛋挞为你收集整理的latex-pgfplots简单绘图基本环境原例创建形态变换的全部内容，希望文章能够帮你解决latex-pgfplots简单绘图基本环境原例创建形态变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。