PGFPlots 是 LATEX 中的一个功能强大的绘图包，其安装的方法详见http://blog.csdn.net/u010450214/article/details/50577929 。在这篇文章中，我们介绍一些 PGFPlots 的基本绘图功能。

1 绘制统计图

统计图常被用于数据分析。下面给出一些用 PGFPlots 绘制统计图的示例。

1.1 线图

线图有折线图和光滑折线图两种，我们用一个例子来演示两种线图的画法。

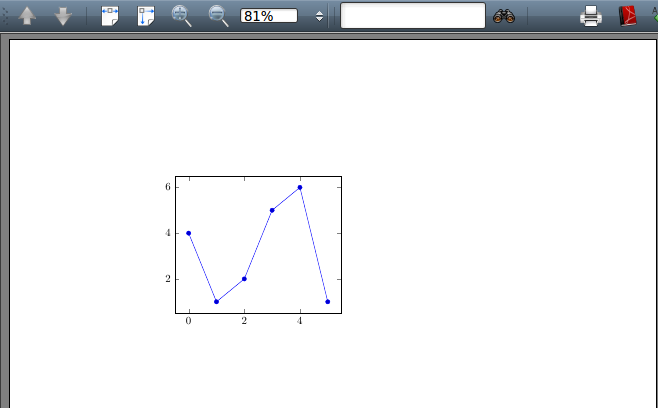
例1 给出一组数据 {(0,4),(1,1),(2,2),(3,5),(4,6),(5,1)} ，绘制经过这些点的两种线图。绘制折线图的代码和结果如下：

documentclass[a4paper]{article}
% 文件类型是A4纸的文章
usepackage{pgfplots}
% 使用pgfplots绘图工具包
pgfplotsset{width=7cm,compat=1.13} % 图片绘制的宽度是7cm,使用的pgfplots版本为1.13
begin{document}
% 文档开始
begin{tikzpicture}
% 绘图开始
begin{axis}
% 添加坐标
addplot+[sharp plot]
% 调用绘图函数，并设置绘图的类型是折线图
coordinates
% 声明是在迪卡尔坐标系中的数据
{
% 输入数据
(0,4) (1,1) (2,2)
(3,5) (4,6) (5,1)
};
end{axis}
% 结束坐标
end{tikzpicture}
% 绘图结束
end{document}
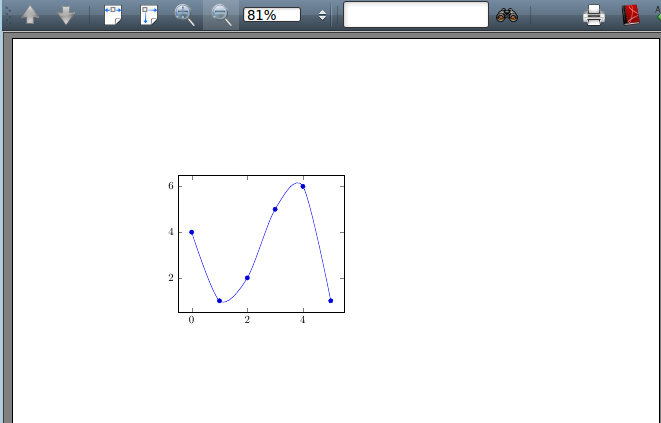
% 文档结束

下面是绘制光滑折线图的代码和结果：

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}
addplot+[smooth]
% 设置绘图的类型是光滑线图
coordinates
{
(0,4) (1,1) (2,2)
(3,5) (4,6) (5,1)
};
end{axis}
end{tikzpicture}
end{document} 

1.2 条形图

条形图常用于展示各项目间的比较结果。

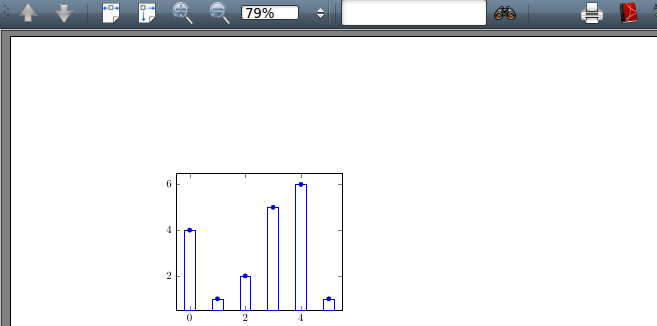
例2 给出一组数据 {(0,4),(1,1),(2,2),(3,5),(4,6),(5,1)} ，绘制一般条形图。代码和结果如下：

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}
addplot+[ybar]
% 绘制关于y坐标的条形图
coordinates
{
(0,4) (1,1) (2,2)
(3,5) (4,6) (5,1)
};
end{axis}
end{tikzpicture}
end{document} 

下面的例子演示如何对条形图进行填充来加强数据间的对比。

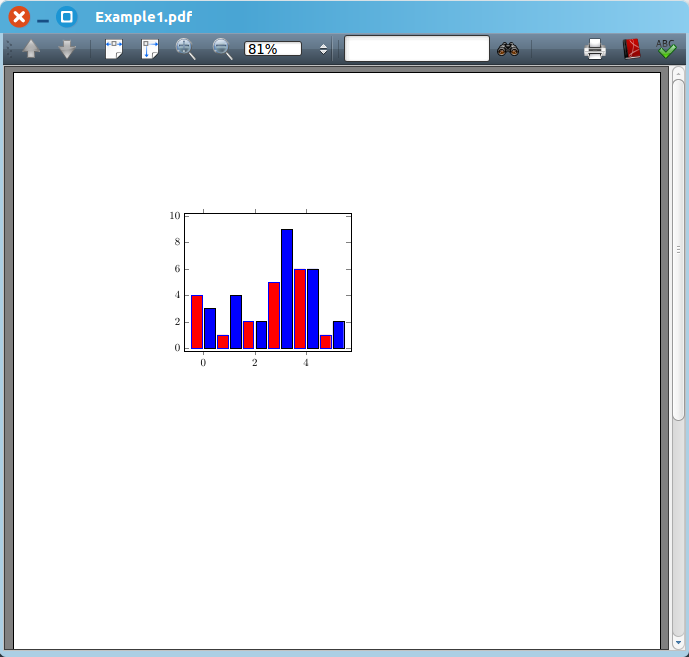
例3 根据数据 {(0,4),(1,1),(2,2),(3,5),(4,6),(5,1)} 绘制蓝色边界、红色填充的条形图；同时，根据数据 {(0,3),(1,4),(2,2),(3,9),(4,6),(5,2)} 绘制黑色边界、蓝色填充的条形图。代码和结果如下：

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}[ybar,enlargelimits=0.15]
% 绘制关于y坐标的条形图，条形之间的最大间隔是0.15cm
addplot[draw=blue,fill=red]
% 蓝色边界、红色填充
coordinates
{
(0,4) (1,1) (2,2)
(3,5) (4,6) (5,1)
};
addplot[draw=black,fill=blue]
% 黑色边界、蓝色填充
coordinates
{
(0,3) (1,4) (2,2)
(3,9) (4,6) (5,2)
};
end{axis}
end{tikzpicture}
end{document} 

1.3 直方图

直方图又称为质量分布图，是最常用统计图之一。直方图的绘制方式与前面两种统计图略有不同，它依赖于 PGFPlots (?) 自身的计算功能。

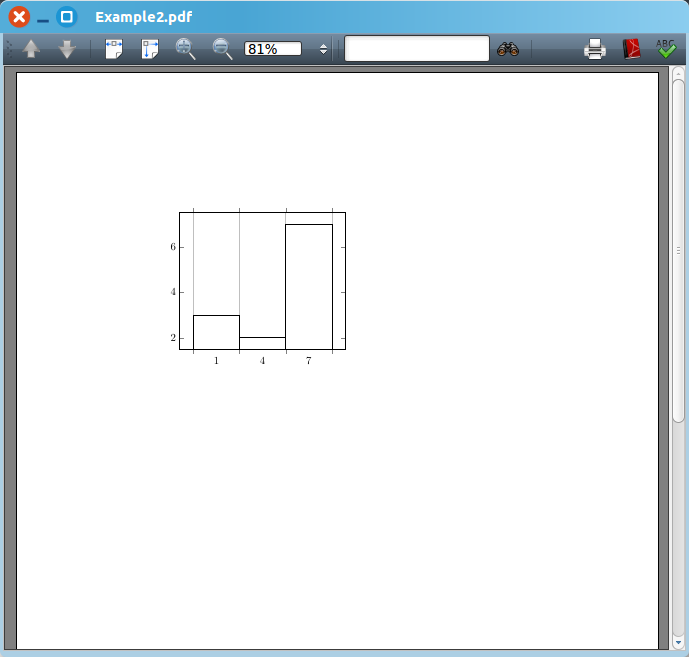
例4 绘制数据 {1,2,1,5,4,10,7,10,9,8,9,9} 的直方图的代码和结果如下：

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}[ybar interval]
% 绘制y条形图，并且分隔出区间
addplot[hist={bins=3}]
% 绘制图像设置为直方图，组距为3
table[row sep=\,y index=0]
% 设置表的行以"\"分隔，y的从0开始
{
data\
% 输入数据
1\ 2\ 1\ 5\ 4\ 10\
7\ 10\ 9\ 8\ 9\ 9\
};
end{axis}
end{tikzpicture}
end{document} 

2 线性回归

在 PGFPlots 中只能拟合一次函数，不能拟合更高次数的函数。下面给出一个示例。

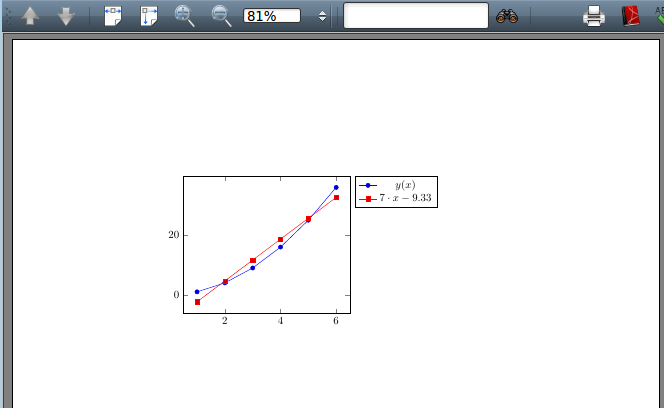
例5 绘制数据 {(1,1),(2,4),(3,9),(4,16),(5,25),(6,36)} 的线性回归绘图，代码和结果如下：

documentclass[a4paper]{article}
usepackage{pgfplots}
usepackage{pgfplotstable}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}[legend pos=outer north east] % 将图例放在图外，位于图的东北角
addplot
table
% 绘制原始数据的折线图
{
% X，Y的原始数据
X Y
1 1
2 4
3 9
4 16
5 25
6 36
};
addplot
table[y={create col/linear regression={y=Y}}] % 对输入的数据作线性回归
{
X Y
1 1
2 4
3 9
4 16
5 25
6 36
};
addlegendentry{$y(x)$}
% 给第一个图像添加图例，即原始函数y(x)
addlegendentry{
% 给第二个图像添加图例，即线性回归结果a*x+b
$pgfmathprintnumber{pgfplotstableregressiona} cdot x
pgfmathprintnumber[print sign]{pgfplotstableregressionb}$}
end{axis}
end{tikzpicture}
end{document} 

3 绘制函数图像

PGFPlots 最重要的功能是绘制函数图像，用它绘制二维和三维函数图像非常的简单。接下来，我们将分别展示一些基本函数图像的绘制。

3.1 二维显式函数图像

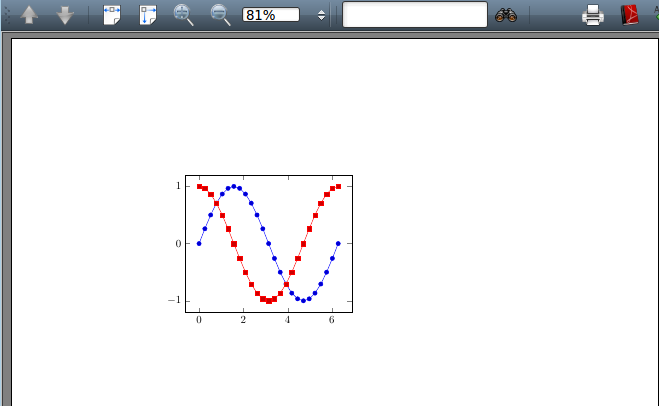
例6 绘制三角函数 f(x)=sinx 和 g(x)=cosx 在定义域 [0,2π] 上的图像。

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}
addplot+[domain=0:2*pi]
% 设置函数的定义域
{sin(deg(x))};
% 输入显式函数
addplot+[domain=0:2*pi]
% 设置函数的定义域
{cos(deg(x))};
% 输入显式函数
end{axis}
end{tikzpicture}
end{document} 

3.2 三维显式函数图像

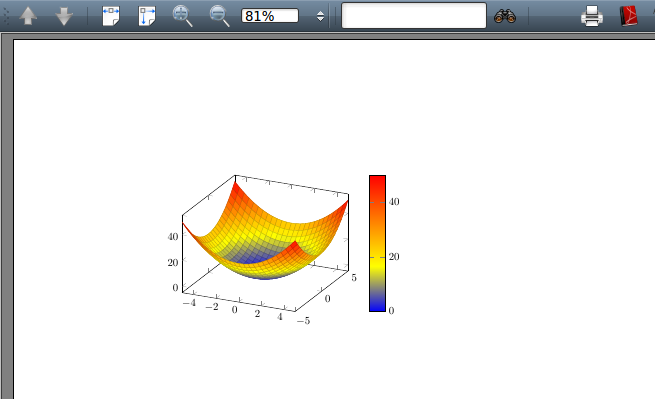
例7 绘制函数 f(x,y)=x2+y2 的三维函数图像。

documentclass[a4paper]{article}
usepackage{pgfplots}
usepgfplotslibrary{colorbrewer}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}[colorbar]
% 绘制坐标，并设置一个彩色指示条
addplot3[surf]
% 绘制三维图
{x^2+y^2};
% 输入二元显式函数
end{axis}
end{tikzpicture}
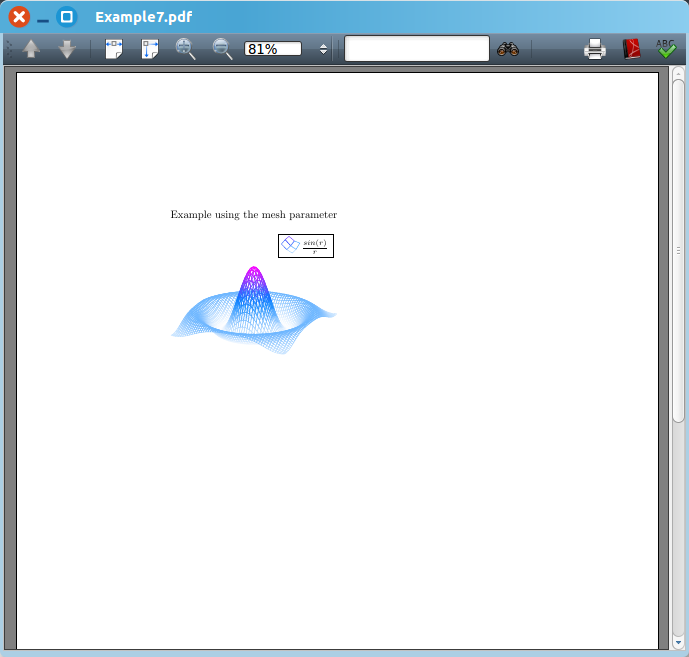
end{document} 

我们也可以绘制一些漂亮而“复杂”的三维图像，如下图的“帽子图”。

documentclass[a4paper]{article}
usepackage{pgfplots}
usepgfplotslibrary{colorbrewer}
pgfplotsset{width=7cm,compat=1.13}
begin{document}
begin{tikzpicture}
begin{axis}[
title=Example using the mesh parameter, %图像的标题
hide axis,
%隐藏坐标
colormap/cool,
%颜色风格
]
addplot3[
mesh,
%绘制的三维图像是网格
samples=50,
%定义域分割数量
domain=-8:8,
%定义域
]
{sin(deg(sqrt(x^2+y^2)))/sqrt(x^2+y^2)};
%二元显式函数
addlegendentry{$frac{sin(r)}{r}$}
%添加图例
end{axis}
end{tikzpicture}
end{document} 

3.3 隐式函数图像

隐式函数图像的绘制非常复杂。（在 Matlab 中，我们可以利用 isosurface 函数直接绘制隐式函数图像。）一般情况下，我们需要先把隐式函数转化成显式函数或者参数方程的形式。接下来，我们给出一个具体的在 PGFPlots 中绘制隐式函数的示例。

例8 绘制隐函数 x2+y2=4 的函数图像。我们将该隐函数转化为参数方程： x=2cosx,y=2sinx ，定义域为 [0,2π] 。

documentclass[a4paper]{article}
usepackage{pgfplots}
pgfplotsset{width=7cm,compat=1.13}
newcommand*{A}{2}
%定义新命令A为2
newcommand*{num}{3}
%定义新命令num为3

pgfmathdeclarefunction{SolutionX}{1}{ % X的参数方程
pgfmathparse{A*(cos(deg(t)))}
}
pgfmathdeclarefunction{SolutionY}{1}{ % Y的参数方程
pgfmathparse{A*(sin(deg(t)))}
}
tikzset{elegant/.style={smooth, red, thick, samples=101}} % 定义风格
begin{document}
begin{tikzpicture}
begin{axis}[axis lines=middle,
% 设置坐标风格
xmin=-num, xmax=num,
% 坐标的范围
ymin=-num, ymax=num,
xlabel=$x$, ylabel=$f(x)$] % 横纵坐标的标签
addplot[elegant,variable=t, domain=-2*pi:0] % 设置图像风格、变量、定义域
({SolutionX(t)},{SolutionY(t)});
% 绘制隐函数的参数方程
end{axis}
end{tikzpicture}
end{document} 

4 补充说明

4.1 条形图与直方图的区别

直方图相邻柱体之间没有间隔，而条形图则有。在条形图中，横轴上的数据是孤立的，是一个具体的数据；而在直方图中，横轴上的数据是连续的，是一个范围。条形图是用条形的高度表示频数的大小；而直方图是用长方形的面积表示频数。

4.2 为什么 PGFPlots 中只能绘制一次线性回归的图像

我猜测这是由计算的复杂度所致。我们可以使用公式我完成一次线性拟合；而二次（及以上）的回归模型是采用最小二乘法来进行拟合的，计算其系数需要求解一个系数矩阵为范德蒙德(Vandermonde)矩阵的线性方程组，计算非常复杂。

4.3 为什么 PGFPlots 中不能直接绘制隐式函数的图像

因为直接绘制隐式函数的图像涉及到求解方程（组），而且往往是求解非线性方程（组），需要的计算量将非常的庞大。比如说，含有两个未知变量的隐函数 f(x,y)=0 ，为了确定 x0 所对应的点 (x0,y0) ，我们需要求解方程 f(x0,y0)=0 ，这通常非常复杂。因此，我们一般都是通过隐式函数的参数方程来进行绘图。而有些隐函数求解参数方程非常难，甚至没有参数方程。总之，隐函数图像的绘制一般比较复杂，这也限制了绘制隐函数图像的工具包的开发。

4.4 一些未解决的疑问

1. 线性回归的函数的实现细节。
2. 哪种绘制隐式函数图像的方法比较好用，是转成参数的形式，还是转化成显式函数的形式？

最后

以上就是外向红酒为你收集整理的PGFPlots绘图简介1 绘制统计图2 线性回归3 绘制函数图像4 补充说明的全部内容，希望文章能够帮你解决PGFPlots绘图简介1 绘制统计图2 线性回归3 绘制函数图像4 补充说明所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。