概述
#1. 模型原理
用神经网络来训练语言模型的思想最早由百度 IDL （深度学习研究院）的徐伟提出[1]，其中这方面的一个经典模型是NNLM（Nerual Network Language Model），具体内容可参考 Bengio 2003年发表在JMLR上的论文[2]
模型的训练数据是一组词序列$ w_{1 } . . . ... ...w_{T} , , ,w_{t} in V$。其中 V V V 是所有单词的集合（即词典）， V i V_{i} Vi 表示字典中的第 i 个单词。NNLM的目标是训练如下模型：
- f ( w t , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = p ( w t ∣ w 1 t − 1 ) f(w_{t},w_{t-1},...,w_{t-n+2}, w_{t-n+1})=p(w_{t} | {w_{1}}^{t-1}) f(wt,wt−1,...,wt−n+2,wt−n+1)=p(wt∣w1t−1)
其中 w t w_{t} wt表示词序列中第 t t t 个单词， w 1 t − 1 {w_{1}}^{t-1} w1t−1表示从第1个词到第 t t t 个词组成的子序列。模型需要满足的约束条件是：
-
f ( w t , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) > 0 f(w_{t},w_{t-1},...,w_{t-n+2}, w_{t-n+1}) > 0 f(wt,wt−1,...,wt−n+2,wt−n+1)>0
-
∑ i = 1 ∣ V ∣ f ( i , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = 1 sum_{i=1}^{|V|}f(i,w_{t-1},...,w_{t-n+2}, w_{t-n+1}) =1 ∑i=1∣V∣f(i,wt−1,...,wt−n+2,wt−n+1)=1
下图展示了模型的总体架构：
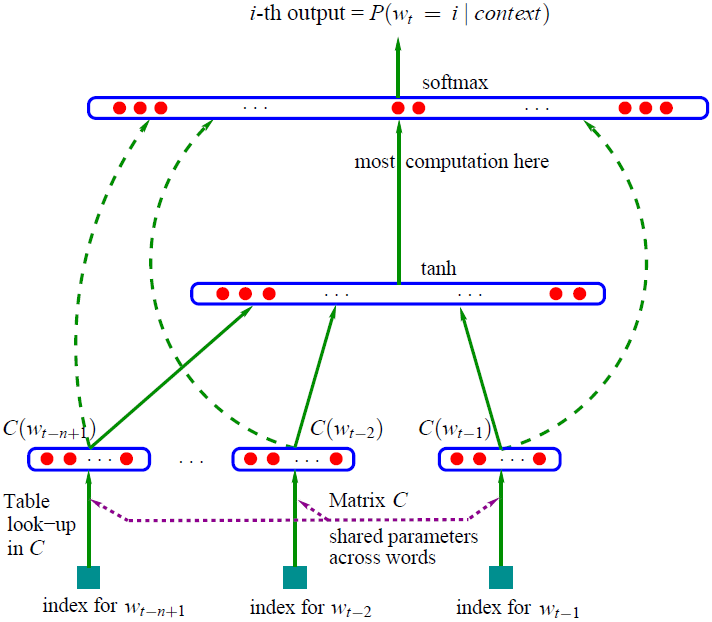
该模型可分为特征映射和计算条件概率分布两部分：
-
特征映射：通过映射矩阵 C ∈ R ∣ V ∣ × m C in R^{|V|×m} C∈R∣V∣×m 将输入的每个词映射为一个特征向量， C ( i ) ∈ R m C(i) in R^{m} C(i)∈Rm表示词典中第 i 个词对应的特征向量，其中 m m m 表示特征向量的维度。该过程将通过特征映射得到的 C ( w t − n + 1 ) , . . . , C ( w t − 1 ) C(w_{t-n+1}),...,C(w_{t-1}) C(wt−n+1),...,C(wt−1) 合并成一个 ( n − 1 ) m (n-1)m (n−1)m 维的向量： ( C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) (C(w_{t-n+1}),...,C(w_{t-1})) (C(wt−n+1),...,C(wt−1))
-
计算条件概率分布：通过一个函数 g g g （ g g g 是前馈或递归神经网络）将输入的词向量序列 ( C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) (C(w_{t-n+1}),...,C(w_{t-1})) (C(wt−n+1),...,C(wt−1)) 转化为一个概率分布 y ∈ R ∣ V ∣ y in R^{|V|} y∈R∣V∣ ，$y $ 中第 i 位表示词序列中第 t 个词是 V i V_{i} Vi 的概率，即：
- f ( i , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = g ( i , C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) f(i,w_{t-1},...,w_{t-n+2}, w_{t-n+1})= g(i,C(w_{t-n+1}),...,C(w_{t-1})) f(i,wt−1,...,wt−n+2,wt−n+1)=g(i,C(wt−n+1),...,C(wt−1))
下面重点介绍神经网络的结构，网络输出层采用的是softmax函数，如下式所示：
- p ( w t ∣ w t − 1 , . . . , w t − n + 2 , w t − n + 1 ) = e y w t ∑ i e y i p(w_{t}|w_{t-1},...,w_{t-n+2}, w_{t-n+1}) = frac{ e^{y_{w_{t}}} }{ sum_{i}^{ }e^{y_{i}} } p(wt∣wt−1,...,wt−n+2,wt−n+1)=∑ieyieywt
其中 y = b + W x + U t a n h ( d + H x ) y = b +Wx + Utanh(d + Hx) y=b+Wx+Utanh(d+Hx)，模型的参数 θ = ( b ， d ， W ， U ， H ， C ) theta = (b，d，W，U，H，C) θ=(b，d，W，U，H，C)。 x = ( C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) x=(C(w_{t-n+1}),...,C(w_{t-1})) x=(C(wt−n+1),...,C(wt−1)) 是神经网络的输入。 W ∈ R ∣ V ∣ × ( n − 1 ) m W in R^{|V|×(n-1)m} W∈R∣V∣×(n−1)m是可选参数，如果输入层与输出层没有直接相连（如图中绿色虚线所示），则可令 W = 0 W = 0 W=0。 H ∈ R h × ( n − 1 ) m H in R^{h×(n-1)m} H∈Rh×(n−1)m是输入层到隐含层的权重矩阵，其中 h h h表示隐含层神经元的数目。 U ∈ R ∣ V ∣ × h U in R^{|V|×h} U∈R∣V∣×h是隐含层到输出层的权重矩阵。 d ∈ R h din R^{h} d∈Rh 和 b ∈ R ∣ V ∣ b in R^{|V|} b∈R∣V∣分别是隐含层和输出层的偏置参数。
**需要注意的是：**一般的神经网络模型不需要对输入进行训练，而该模型中的输入 x = ( C ( w t − n + 1 ) , . . . , C ( w t − 1 ) ) x=(C(w_{t-n+1}),...,C(w_{t-1})) x=(C(wt−n+1),...,C(wt−1)) 是词向量，也是需要训练的参数。由此可见模型的权重参数与词向量是同时进行训练，模型训练完成后同时得到网络的权重参数和词向量。
#2. 训练过程
模型的训练目标是最大化以下似然函数：
- L = 1 T ∑ t l o g f ( w t , w t − 1 , . . . , w t − n + 2 , w t − n + 1 ; θ ) + R ( θ ) L=frac{1}{T} sum_{t}^{ } logf(w_{t},w_{t-1},...,w_{t-n+2}, w_{t-n+1}; theta) + R(theta) L=T1∑tlogf(wt,wt−1,...,wt−n+2,wt−n+1;θ)+R(θ) ，其中 θ theta θ为模型的所有参数， R ( θ ) R(theta) R(θ)为正则化项
使用梯度下降算法更新参数的过程如下：
-
θ
←
θ
+
ϵ
∂
l
o
g
p
(
w
t
∣
w
t
−
1
,
.
.
.
,
w
t
−
n
+
2
,
w
t
−
n
+
1
)
∂
θ
theta leftarrow theta +epsilon frac{partial logp(w_{t}|w_{t-1},...,w_{t-n+2}, w_{t-n+1}) }{partial theta}
θ←θ+ϵ∂θ∂logp(wt∣wt−1,...,wt−n+2,wt−n+1) ,其中 $epsilon $为步长。
#3. 参考资料
[1] Can Artificial Neural Networks Learn Language Models?
[2] A Neural Probabilistic Language Model
http://blog.sina.com.cn/s/blog_66a6172c0102v1zb.html
最后
以上就是狂野冰棍为你收集整理的神经网络语言模型（NNLM）的全部内容，希望文章能够帮你解决神经网络语言模型（NNLM）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复