神经概率语言模型

74 阅读 0 评论 49 点赞

我是靠谱客的博主雪白小蘑菇，最近开发中收集的这篇文章主要介绍神经概率语言模型，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

摘要

统计语言建模的目标是学习语言中单词序列的联合概率函数。由于 the curse of dimensionality，这本质上是困难的：模型测试的单词序列可能与训练集中的单词序列不同。一种基于n-gram的传统的但非常成功的方法是，通过连接训练集中看到的非常短的重叠序列来获得泛化。我们建议通过学习词的分布式表示来对抗维数灾难，模型通过训练语句对指数级语义相关的句子进行建模，该模型同时学习每个单词的分布式表示以及单词序列的概率函数。如果单词序列是由已经见过的单词（在具有附近表示的意义上）的相似单词构成的，那么获得泛化是因为这些之前从未见过的单词序列具有较高的概率。在合理的时间内训练这样的大型模型（具有数百万个参数）本身就是一个重大挑战。本文介绍了使用神经网络进行概率函数的实验，改进了n-gram模型，可以利用更长的上下文，并在两个文本预料上都显示了很好的效果。。
分布式表示：将庞大的词汇表，从一个高维空间映射到一个低维空间中，而又尽量保存不同词之间差异性的技术。所谓分布式表示，是存在一个分布式假设，即如果两个词的上下文相同，那么这两个词的表示也是相似的。可以将分布式表示理解为一种用来得到词表示的方法。

Introduction

使语言建模和其他学习问题实现困难的根本问题是维度灾难。当人们想要模拟许多离散随机变量（例如句子中的单词或数据挖掘任务中的离散属性）之间的联合分布时，更为明显。例如，如果想用大小为100,000的词汇表V的自然语言来模拟10个连续单词的联合分布，则可能有 $100000^{10} - 1 = 10^{50} - 1$ 个自由参数。在对连续变量建模时，我们更容易获得泛化（例如，使用平滑的函数类，如多层神经网络或高斯混合模型），因为要学习的函数的预期具有一些局部平滑性。对于离散空间，泛化结构并不那么明显：这些离散变量的任何变化都可能对要估计的函数的值产生巨大影响，并且当每个离散变量可以采用的数值很大时，在 Hamming 距离中的大多数观测对象几乎彼此远离。
从非参数密度估计的观点出发，想象不同学习算法是如何泛化的，一种有用方法是考虑最初集中在训练点（例如，训练句子）的概率质量（mass）是如何以更大的体积分布，通常在训练点周围的相邻的某种形式。在高维度中，将概率质量分布在重要的地方而不是在每个训练点周围的所有方向上均匀分布是至关重要的。在本文中，我们将展示这里提出的方法的通用方式与以前的最先进的统计语言建模方法一般化的方式是根本不同的。
语言的统计模型可以由给定所有先前的单词的下一个单词的条件概率表示:
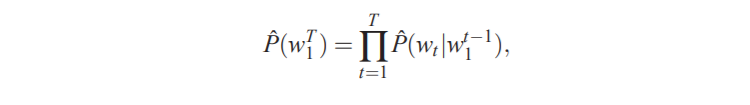
其中 $w_{t}$ 是第 t 个词， $w^{j}_{i} =（w_{i}，w_{i + 1}，...，w_{j-1}，wj)$ 表示子序列。这种统计语言模型在涉及自然语言的许多技术应用中是有用的，例如语音识别，语言翻译和信息检索等。因此，统计语言模型的改进可能对此类应用产生重大影响。
在构建自然语言的统计模型时，通过利用单词顺序大大降低了这种建模问题的难度，并且在单词序列中时间上更接近的单词在统计上更加依赖。因此，对于大量上下文中n-1个单词的组合，n-gram模型构造出了下一个单词的条件概率表：
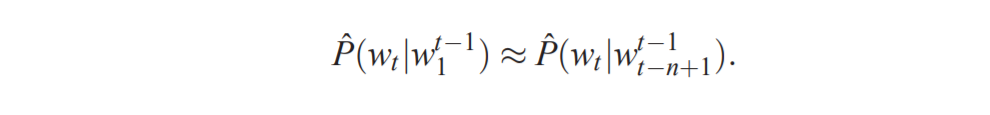
我们只考虑实际出现在训练语料库中的那些连续单词组合，或者那些足够频繁发生的组合。但当出现n个词的新组合但在训练语料库中没有发现时会发生什么？我们不希望为这种情况分配零概率，因为这样的新组合可能会发生，并且对于更大的上下文，它们将更频繁地发生。一个简单的办法是使用更小的语料进行概率预测，例如后退三元模型或平滑三元模型。那么，在这样的模型中，从训练语料库看到的单词序列到新的单词序列中，泛化是如何获得的？理解这种情况的方法是考虑相应的插值 (interpolated) 或n元回退（back-off n-gram）模型的生成模型，通过“粘合(gluing)”训练数据中短且重复的长度为1,2甚至n个频繁出现的单词来生成新的单词序列。
通常研究人员使用n = 3，即三元，可以获得最先进的结果，但Goodman（2001）结合了许多技巧可以产生实质性的改进。显然，序列中有更多信息紧跟在预测词之前，而不仅仅是前两个词的标识。这种方法至少有两个地方需要改进，首先，它没有考虑超过1或2个单词的上下文，第二没有考虑单词之间的“相似性”。例如，在训练语料库中看到“The cat is walking in the bedroom”的句子应该可以帮助我们概括地使句子“A dog was running in a room”出现的概率变高，因为“dog”和“cat”(“the”和“a”，“room”和“bedroom”等等）具有相似的语义和语法角色。
已经提出了许多方法来解决这两个问题，我们将在1.2节中简要解释这里提出的方法与其中一些早期方法之间的关系。我们将首先讨论提出的方法的基本思想是什么。第2节将更正式的介绍，使用依赖于共享参数的多层神经网络来实现。本文的另一个贡献是考虑如何为非常大的数据集（具有数百万或数千万个示例）训练这种非常大的神经网络（具有数百万个参数）。最后，本文的一个重要贡献是表明：训练这种 large-scale 模型虽然昂贵但是可行的，可扩展到 large contexts，并能产生良好的比较结果。
本文中的许多操作都是矩阵表示法，小写字母 v 表示列向量， $v^{'}$ 表示其转置， $A_{j}$ 表示矩阵A的第j行，并且 $x . y$ = $x^{'}y$ 。

1.1 Fighting the Curse of Dimensionality with Distributed Representations

简而言之，提出的方法的思想可以概括如下：
1 为每一个在词典中的单词赋一个实值向量，向量的维度一般取30，60，100。
2 根据序列中单词的特征向量来构建单词序列的联合概率函数
3 同时学习单词特征向量和该概率函数的参数
特征向量表示单词的不同方面：每个词与向量空间中的一点相关联。特征的数量（例如，在实验中m = 30,60或100）远小于词汇的大小（例如17,000）。概率函数表示用给定的先前词预测下一个单词的条件概率（例如，在实验中使用多层神经网络来预测给定先前词的下一个单词）。该函数具有可以迭代调整的参数，以便最大化训练数据的对数似然或正则化标准，例如:增加一个权值衰减惩罚（weight decay penalty）。学习与每个单词相关联的特征向量，并使用语义特征的先验知识来初始化它们。(The feature vectors associated with each word are learned, but they could be initialized using prior knowledge of semantic features.)
它为什么有效？在前面的例子中，如果我们知道狗和猫扮演类似的角色（语义和语法）,并且类似地(the,a)、(bedroom,room)、(is,was)、(running,walking)，我们可以自然地推广（即转移概率质量）从

The cat is walking in the bedroom
到 A dog was running in a room
并且类似的 The cat is running in a room
A dog is walking in a bedroom
The dog was walking in the room
…

和许多其他的组合。在所提出的模型中，具有相近语意的单词具有相近的特征向量，如果特征向量有一个小的变化，则在概率模型中也会体现出来。因此，训练数据中任意一个存在的上述句子不仅会增加该句子的概率，还会增加句子空间（由特征向量序列表示）上的其组合数量的“邻居”的概率。

1.2 与先前工作的关系（Relation to Previous Work）

已经发现使用神经网络的思想去对高维离散分布进行建模是对学习 $Z_{1}···Z_{n}$ 的联合概率有用的。其中， $Z_{1}···Z_{n}$ 是一组随机变量，其中每个变量可能具有不同的性质。在该模型中，联合概率被分解为条件概率的乘积：

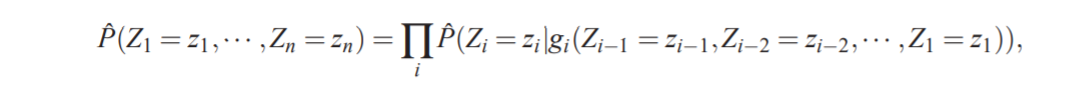
其中g（x）是由从左至右架构的神经网络表示的函数，第i个输出块 $g_{i}()$ 的计算参数用于表示给定之前Z值， $Z_{i}$ 的条件分布。这个方法在四个UCI数据集上可以工作的很好。为了能够处理可变长度的数据，例如句子，因此必须对上述方法做出调整。另一个重要的区别是，所有的 $Z_{i}$ （第i个位置的单词），指的是同一类型的对象（一个单词）。因此，这里提出的模型引入了跨时间的参数共享，即跨时间使用相同的 $g_{i}()$ ，即在不同位置的输入词之间使用。我们在这里大力推广这个想法，并专注于学习单词序列分布的统计模型，而不是学习单词在句子中的作用。这里提出的方法还涉及先前基于字符的文本压缩的提议，其使用神经网络来预测下一个字符的概率。模型由于没有隐藏单元和单个输入词而被限制为捕获单数据和二元数据统计。
发现词之间的某些相似性以获得从训练序列到新序列的泛化的想法并不新鲜。例如，它在基于学习单词聚类的方法中被利用：每个单词都确定性地或概率地与离散类相关联，并且同一类中的单词在某些方面相似。在这里提出的模型中，我们不是用离散的随机或确定性变量（对应于单词集的软分区或硬分区）来表征相似性，而是为每个单词使用连续的实数向量，即一个学习的分布式特征向量(learned distributed feature vector)，表示单词之间的相似性。
在信息检索领域中，对单词使用向量空间表示的想法已经被很好地利用，其中单词的特征向量是根据它们在同一文档中共同处现的概率来学习的。一个重要的区别是，在这里，我们寻找一个有代表性的词，该词有助于紧凑地表示自然语言文本中的单词序列的概率分布。

2.一个神经模型

训练模型： $f(w_{t},...,w_{t-n+1}) = hat{P}(w_{t}|w^{t-1}_{1})$ (用前n-1个词预测下一个单词wt)
其中，训练集由 $w_{1}...w_{t}$ 序列组成， $w_{t}$ ∈V，词表V是巨大的但有限的集合。
困惑度： $frac{1}{hat{P}(w_{t}|w^{t-1}_{1})}$ ，这也是平均负对数似然的指数
对模型的唯一约束是对于 $w^{t-1}_{1}$ 的选择， $sum_{i=1}^{|V|}f(i,w_{t-1},...,w_{t-n+1}) = 1$ ，其中 f > 0 。通过这些条件概率的乘积，可以获得单词序列的联合概率的模型。
将模型分解为两个部分：

一个映射C，从词表中的任意元素i到实向量C(i)∈ $R^{m}$ 中，这个实值向量就是所要学习的 distributed representation ，该向量表示词汇表中每个词的分布式特征向量。C是一个大小为|V|×m的自由参数矩阵。(随机初始化)
函数g将上下文单词的特征向量 $C(w_{t−n+1}),...,C(w_{t−1}))$ 作为输入序列，将它们映射为V中下一个单词 $w_{t}$ 的条件概率分布: $f(i,w_{t-1},...,w_{t-n+1}) = g(i,C(w_{t−1}),...,C(w_{t−n+1}))$ 。g的输出是第i个单词的估计概率向量 $hat{P}(w_{t}|w^{t-1}_{1})$ 。如下图所示：

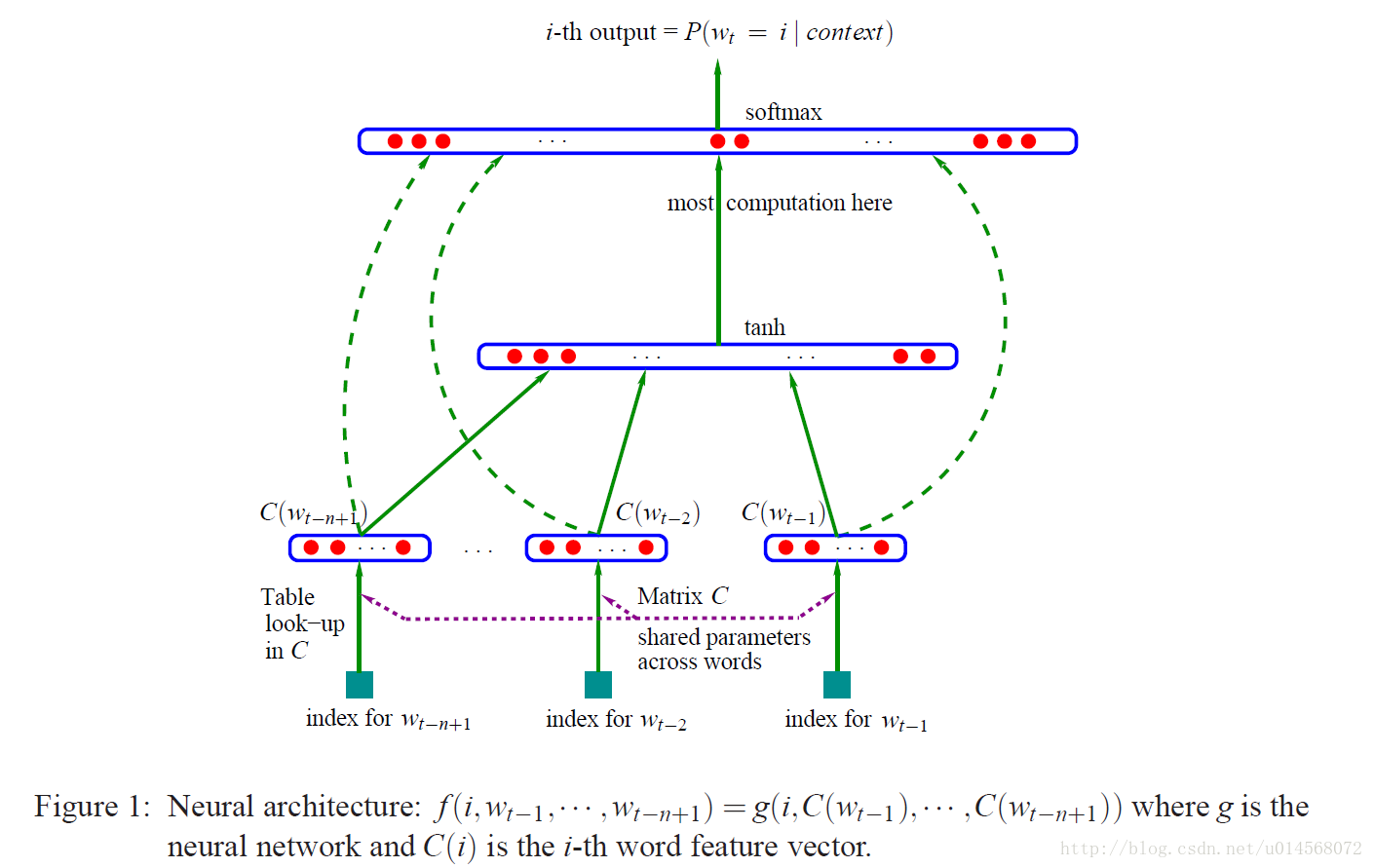
函数f是映射C和g的组合，C在上下文所有单词间共享。矩阵C的第i行对应第i个单词的特征向量C(i)。函数g通过带有参数ω的前馈或递归神经网络或其他参数化函数来实现。整体参数集θ=(C,ω)。
训练通过最大化训练语料库的惩罚似然估计θ来实现：

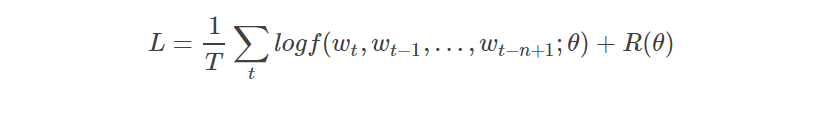
其中R(θ)是正则项。例如，在我们的实验中，R是仅用于衡量神经网络和矩阵C的权重衰减惩罚，而不是偏差。
在模型中，自由参数的数量仅与词汇表中的单词数量V线性相关，自由参数的数量也是序列长度n的线性函数。

在下面大部分实验中，神经网络具有一个隐藏层，隐藏层在词特征映射的前面。并且可选的，词特征层可以直接连接到输出层。因此实际存在两层隐藏层：共享词特征层C，和普通的双曲正切隐藏层。神经网络的输出层使用softmax计算以下函数以保证正概率总和为1：

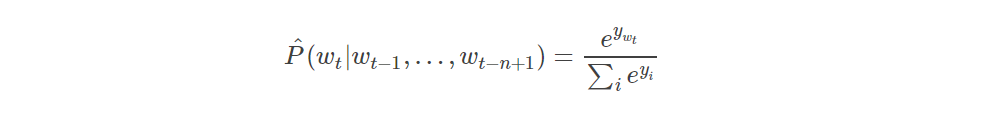
$y_{i}$ 是对于每个输出单词i计算的未归一化log概率，由下列式子来计算：
$y = b + W x + U t a n h (d + H x)$
其中双曲正切tanh逐元素地应用，x是单词特征层激活向量(word features layer activation vector)，是来自矩阵C的输入字特征的串联：
$x = (C(w_{t-1}),C(w_{t-2}),...,C(w_{t-n+1}))$
令h为隐藏层单元的数量，m是每个单词的特征的数量。当单词特征向量与输出之间不直接连接时，W被设置为0。模型的自由参数有：输出偏差 $b_{|v|×1}$ ，隐藏层偏差 $d_{h×1}$ ，隐藏层到输出层的权重 $U_{|V|×h}$ ，单词特征到输出层的权重 $W_{|V|×(n-1)m}$ ，隐藏层权重 $H_{h×(n-1)m}$ ，和单词特征 $C_{|V|×m}$ ：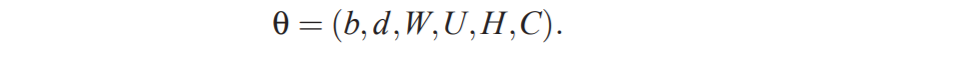
自由参数的个数是 $∣ V ∣ (1 + n m + h) + h (1 + (n - 1) m)$ 。注意理论上来说，如果W和H存在权重衰减而C没有，那么W和H可以向零收敛，而C将会爆炸（blow up）。在实践中，当使用随机梯度上升来训练时，我们没有观察到这种现象。神经网络中的随机梯度上升执行以下迭代更新：

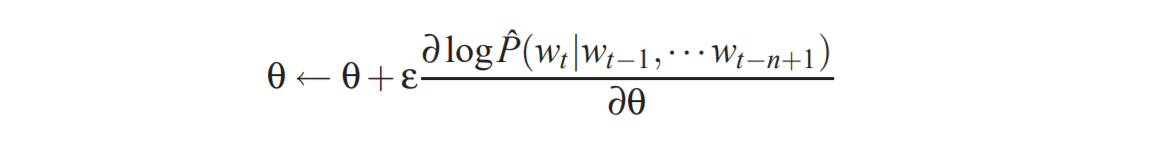
其中，ε是学习率。请注意，在每个示例之后，不需要更新或访问大部分参数：输入窗口中没有出现的所有单词j的单词特征C(j)。
混合模型：在我们的实验中（参见第4节），我们通过将神经网络的概率预测与插值的三元模型的概率预测相结合，可以改进性能。简单的学习权重（验证集上的最大似然）或一组以上下文的频率为条件的权重为0.5。
简单概括：
1. 图中最下方的 $w_{t-n+1}, …, w_{t-2}, w_{t-1}$ 就是前n-1个词，现在要根据这n-1个词预测下一个词 $w_{t}$ 。C(w)是词w对应的特征向量，从w到C(w)的转化就是从矩阵C中取一行。m表示词向量的维度，|V|表示词表的大小（语料中的总词数），h表示隐藏层单元的数量。
2. 在网络的第一层，将 $C(w_{t-n+1}), …, C(w_{t-2}), C(w_{t-1})$ 这n-1个输入向量连接起来，形成一个(n-1)×m维的向量，记为 $x$ 。
3. 网络的第二层（隐藏层）就如同普通的神经网络，直接使用d+Hx得到，其中d是一个偏执项。然后使用tanh作为激活函数。
4. 网络的第三层(输出层)一共有|V|个节点，每个节点 $y_{i}$ 表示下一个词为 i 的未归一化 log 概率。最后使用 softmax 激活函数将输出值 y 归一化成概率。最终，y 的计算公式为： $y = b + W x + U t a n h (d + H x)$
5. 现在万事俱备，用随机梯度下降法把这个模型优化出来就可以了。需要注意的是，一般神经网络的输入层只是一个输入值，而在这里，输入层 x 也是参数（存在于C 中），也是需要优化的。优化结束之后，词向量有了，语言模型也有了。

3.并行实施（Parallel Implementation）

即使参数的数量是输入窗口大小n和词表大小|V|的线性函数，即已经被限制的很好，但是计算的总量还是远远大于n-gram。主要原因是在n-gram模型中，获得特定的p(wt|wt-1,…,wt-n+1)不需要计算词表中所有的概率，因为简单的归一化。神经网络计算的瓶颈主要是在输出层。运行模型（在训练和测试时）在一个并行化的计算机中是减少计算时间的方法，我们在两种平台上探索了并行化：贡献内存处理器和Linux集群。

3.1参数并行处理

如果并行计算机是一个CPU的网络，我们通常支付不起过于频繁的参数交换的开销，因为参数的规模是百兆级别的，这将消耗大量的时间。取而代之我们选择参数并行处理，特别的，参数是输出单元的参数，因为这是在我们的架构中绝大多数计算发生的地方。每个CPU负责计算一个未正则化概率的输出子集。这种策略允许我们实现一个通信开销微不足道的并行的随机梯度下降算法。CPU本质上需要交换两种数据：（1）输出层的正则化因子，（2）隐藏层的梯度和词特征层。所有的CPU都复制在输出层之前的计算，然而这些计算比起总的计算量是微不足道的。
对于单个示例 $w_{t-n + 1}，...，w_{t}）$ ，下面概述了并行化算法，由CPU $i$ 在M个处理器的集群中并行执行。其中，CPU $i$ (i∈(0,M-1))负责计算输出单元起始号为start_i = i × $⌈ ∣ V ∣ / M ⌉$ ，长度为min( $rceil，|V|-start_{i})$ 的输出层块。
公式推导
主要是对上面反向更新利用的梯度上升进行公式推导，计算图如下所示：

由于L = $log_{e}P_{w_{t}} = log_{e}frac{e^{y_{j==w_{t}}}}{sumlimits_{j}e^{y_{j}}} = y_{j==w_{t}} - log_{e}sumlimits_{j}e^{y_{j}}$
(此处的 $e^{y_{j==w_{t}}}中的"=="$ 表示关系运算符，若两者相等则为1；否则为0)
从而， $frac{∂L}{∂y_{i}} = 1_{j==w_{t}} - frac{e^{y_{j}}}{sumlimits_{j}e^{y_{j}}}$ = $1-y_i qquad & 当i等于w_t \ -y_i qquad & a le 0 end{cases}$

由于， $y_i = b_j +aU_j$ ，

$frac{∂L}{∂b_{j}} = frac{∂L}{∂y_{i}} frac{∂y_i}{∂b_{j}} = frac{∂L}{∂y_{i}}$
因此，对b_j进行梯度更新：b_j ← b_j + ε $frac{∂L}{∂y_{i}}$
$frac{∂L}{∂y_i}U_j$ ，对其进行梯度更新： $frac{∂L}{∂y_i}U_j$
$frac{∂L}{∂U_j} = frac{∂L}{∂y_i} frac{∂y_i}{∂U_j} = frac{∂L}{∂y_i} a$ ，对矩阵U进行梯度更新: $U_j ← U_j + εfrac{∂L}{∂y_i} a$

由于， $a_k = tanh(o_k)$ 而tanh(x)的导数为：1-(tanh(x))²，因此

$frac{∂L}{∂o_k} = frac{∂L}{∂a_k} frac{∂a_k}{∂o_k} = (1-a^2_k)frac{∂L}{∂a_k}$

由于，o = d + Hx，

$∂ L ∂ d = ∂ L ∂ o ∂ o ∂ d = ∂ L ∂ o frac{∂L}{∂d} = frac{∂L}{∂o} frac{∂o}{∂d} = frac{∂L}{∂o}$ ，因此： $d ← d + ε ∂ L ∂ o d ← d + εfrac{∂L}{∂o}$
$x^T$ ，因此： $εfrac{∂L}{∂o}x^T$
$H^T$ ，因此： $H^T$

最后，由于x = $C(w_{t−n+1}),...,C(w_{t−1}))$ ，从而 $frac{∂L}{∂C(w_{t-k})} = frac{∂L}{∂x(k)} frac{∂x(k)}{∂C(w_{t-k})} = frac{∂L}{∂x(k)}$ ，因此： $C(w_{t-k}) ← C(w_{t-k}) + εfrac{∂L}{∂x(k)}$

其中 $frac{∂L}{∂C(w_{t-k})}$ 是向量 $∂ L ∂ x frac{∂L}{∂x}$ 的第k个分量

权重惩罚正则化（R(θ)）没有在上面显示，但是可以简单的被实现。需要注意的是参数的更新是立即的而不是通过一个参数梯度向量，这样做可以提高速度。

在前向计算阶段，会出现一些问题，其中一个问题是 $p_{j}$ 可以全部为0，或者他们的其中一个非常大而不能进行指数运算。为了避免这个问题，通常的解决方案是在取得softmax中的指数之前，减去y_i中的最大值。因此我们可以在计算p_j之前加上一个Allreduce运算去在M个处理器间共享y_j的最大值。令q_i为块i中y_j的最大值，然后，在M个处理器之间共同计算并共享总体最大值$Q= max_i q_i 。然后如下计算指数：p_j ← $e^{yj−Q}$ (来代替p_j ← $e^{yj}$ )。

在低速度的集群上，仍然可以获得有效的并行化。与其在每个训练样例计算时通信，不如在每K个训练样例计算时通信。这需要保存神经网络的K个激活和梯度。在K个训练样例的前向阶段后，概率的和必须共享给处理器。然后K后向阶段被初始化。在交换了这些梯度向量之后，每个处理器可以完成后向阶段并更行参数。如果K过大，将会导致不收敛的问题。

4.实验结果

在Brwon语料库上的1181041个词序列上进行了对比实验。前800000个词用来训练，接下来的200000个词用来调整模型的参数，剩下的181041用来测试。不同的词的数量是47587。词的频率3的被合并成为一项。把词表的大小缩小到了|V|=16383。

一个实验也在1995和1996的AP news的文本数据上运行。训练集是大约1400万的序列，发展集的大小大约是100万的序列，测试集也是100的序列。数据有148721个不同的词，我们把词表缩小到|V|=17964，使用的方法是保留高频率的词，把大写字母转化为小写字母，把数字和特殊字符合并等。

对于神经网络，初始的学习速率被设置为 $ε_{0}=0.001$ ，并且逐渐的采用公式 $ε_{t}=ε_{0}/(1+rt)$ 缩小,其中t代表已经被更新的参数数量，r是衰减因子，取值为 $10^{-8}$ 。

4.1 N-Gram模型

第一个对照的对象是使用插值法和平滑法的trigram模型。模型的条件概率表示为:
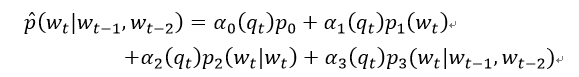
在这里插入图片描述
条件权重 $α_{i}(q_{t})≥0，sum_{i}αi(q_{t})= 1$ 。基本预测值如下：p₀= 1/| V |，p₁(i)是unigram（训练集中单词i的相对频率）， $p_{2}(i|j)$ 也是一个unigram(（当上一个单词是j 时，单词 i 的相对频率)。 $p_{3}(i|j,k)$ 是 unigram(当前两个词是j、k时，单词 i 的相对频率)。这么做的原因是：当 $w_{t-1}，w_{t-2}）$ 的频率大时，p₃最可靠；而当它更低时，p₂，p₁或甚至p₀更可靠。对于q_t（它们是上下文频率区间）的每个离散值，在一组数据（验证集）中，大约5次的EM算法的迭代可以轻松估计他们，而不是去估计单字组，双字母和三字母相对频率。内插的n-gram用于与MLP形成混合，因为它们似乎以非常不同的方式产生“错误”。

4.2 Results

下图为基于困惑度的对不同模型的测试结果：
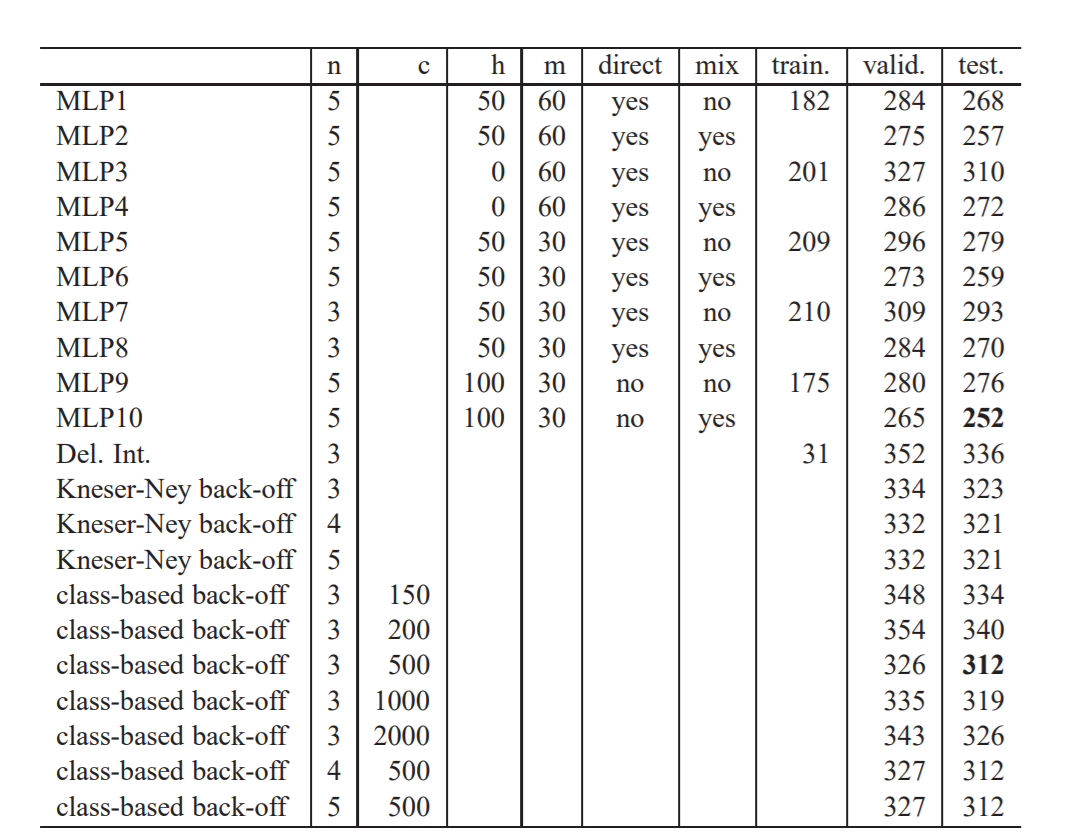
在这里插入图片描述
上图是布朗语料库的比较结果。The deleted interpolation trigram 比具有最低验证困惑度的神经网络的测试困惑度高33％。在最佳n-gram（具有500个单词类的基于类的模型）的情况下，差异为24％。其中，
n：模型的顺序。
c：基于类的n-gram中的单词类数。
h：隐藏单元的数量。
m：MLP的单词特征数，基于类的n-gram的类数。
direct：是否存在从字功能到输出的直接连接。
mix：神经网络的输出概率是否与trigram的输出混合（每个的权重为0.5）。
最后三列给出了训练，验证和测试集的困惑。

5.结论

实验在两个语料库上进行，一个具有超过一百万的训练样例，另一个更大有一千五百万词。实验显示了本论文提出的方法获得了比先进的trigram好很多的困惑度值。

我们相信主要的原因是该方法允许学习分布表示来解决维数灾难的问题。这个模型可能有更多的可以改进的地方，在模型的架构方面，计算效率方面和先验知识的运用方面等。将来的优先研究点应该是提高训练速度。一个简单的想法来利用时间结构并扩展输入窗口的大小的方法是利用卷积神经网络。更一般的在这里介绍的工作打开了提高统计语言模型方法的大门，用基于分布表示的更加平滑的表示方法代替条件概率表。鉴于统计语言模型研究的很多努力工作都花费在了限制和总结条件变量上，来防止过拟合问题，在本论文中介绍的方法转移了这个困难：更多的计算被需要，但是计算和内存需求规模都是线性的，而不是条件变量的指数级别。

最后

以上就是雪白小蘑菇为你收集整理的神经概率语言模型的全部内容，希望文章能够帮你解决神经概率语言模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：NLP
浏览次数：74 次浏览
发布日期：2023-12-31 09:10:23
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_23_ocf0_13_z_26_5.html

神经概率语言模型

概述

摘要

Introduction