自然网络语言模型(NNLM)

在一语料库中, 假设有长度为 T 的文本序列 $S:=w_1，w_2,\cdots ,w_T$. 如果选子序列 $S:=w_{t-1}，w_{t-2},\cdots ,w_{t-n+1}$, 想预估 词汇 $w_t$ 出现的概率, 即计算条件概率
$$P(w_t|w_{t-1}，w_{t-2},\cdots ,w_{t-n+1}).$$
可以使用 NNLM 的方法, 其工作流程见下图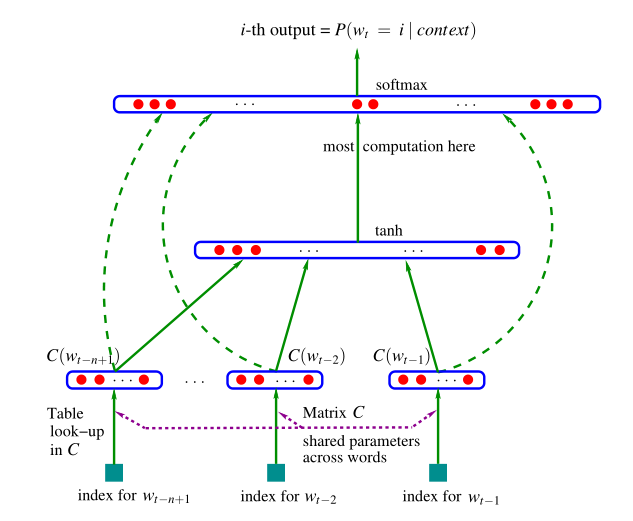
我们先假定语料库生成的 词汇共有 v 个, 则 每个词汇的 1-hot 为 v-维行向量.
第一步, 将 词向量 $w_i$, $i=t-1,\cdots ,t-n+1$, 投放到 d-维向量空间, d由个人选定. 此处使用的是 $v\times d$ 矩阵C. 输出为 $w_{i}C$, 将 n-1 个输出按顺序拼接成 $(n-1)d$-维 行向量 x.

第二步, 将 x 输入到 tanh层中, 这是一个隐含层, 神经元个数可以自己选定设为 h. 于是有一 $h\times (n-1)d$ 的转移 矩阵, 设为 H. 这个层的输出为 h-维 向量 y’=tanh(xH+ b’).

第三步, 将 $x,y^{\prime }$ 输入sigmoid 层, 输出为 一个行向量 y_t, 输出的维度是 v. 这里 两个转移矩阵 $W_{(n-1)d\times v}$, $U_{h\times v}$.
$$y_t=sigmoid(b+xW+y^{\prime }U).$$

使用最大似然估计计算 参数的值.
假定 $w_t$ 的索引是 $i_t$, 令 $y_t(i_t)$ 表示 $y_t$ 的第 $i_t$个分量, 也即预测为 $w_t$ 的概率. 希望 ${\prod }_{t=1}^T{y}_t(i_t)$ 取最大值,
使用 log 后, 取均值, 变成希望
$$L(H,b^{\prime },W,b,C):=\frac{1}{T}\sum log{y}_t(i_t)$$

取最值.

最后

以上就是爱笑彩虹为你收集整理的自然网络语言模型(NNLM)的全部内容，希望文章能够帮你解决自然网络语言模型(NNLM)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。