NOIP2018模拟赛

T1 字符串（string）

【题目描述】

定义两个字符串A,B相似当且仅当满足以下两个条件中的至少一个： (1)A和B相同； (2)将A分为长度相同的两个子串A0,A1，将B分为长度相同的两个子串B0,B1，满足A0相似于B0，A1相似于B1或A0相似于B1，A1相似于B0。 给定两个字符串S,T，问它们是否相似。 有多组数据。

【输入数据】

第一行一个整数t表示数据组数。 每组数据第一行一个字符串S，第二行一个字符串T，保证它们长度相同。

【输出数据】

每组数据一行，若相似输出YES，不相似输出NO。

【样例输入】

2
abab
baab
aabb
abab

【样例输出】

YES
NO

【数据范围】

对于30%的数据，|S|<=30。
对于60%的数据，|S|<=100。
对于100%的数据，t<=30，∑|S|<=500000。

分析

这道题二分，可以乱搞，但是题目绝对绝对绝对绝对有问题，哼

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
using namespace std;

typedef long long ll;
string a,b;
int t;

bool run(string c,string d)
{
	 if(c.length() == 2 && d.length() == 2)
	 {
	 	 if((c[0] == d[0] && c[1]==d[1]) || (c[0]==d[1] && c[1]==d[0]))return 1;
         else return false;
     }
     if(c.length() % 2 && d.length() % 2)
     {
         if(c == d)return 1;
         else return false;
     }
     string lc,rc;
     string ld,rd;
     lc = c.substr(0, c.size()/2);
     rc = c.substr(c.length()-lc.length(), c.size()/2);
     ld = d.substr(0, d.size()/2);
     rd = d.substr(d.length()-ld.length(), d.size()/2);
     if((lc==ld&&rc==rd) || (lc==rd&&rc==ld)) return 1;
     if((run(lc,ld) && run(rc,rd)) || (run(lc,rd) && run(ld, rc))) return 1;
     else return 0;
     
}

int main()
{
//	freopen("string.in","r",stdin);
//	freopen("string.out","w",stdout);
	scanf("%d", &t);
	while(t--)
	{
	   a=""; b="";
	   cin >> a;
	   cin >> b;
	   if(a == b)
	   {
	   		printf("YESn");
	   		continue;
	   }
       if(a.length() % 2)
       {
       		printf("NOn");
           continue;
       }
       if(run(a,b)) printf("YESn");
	   else cout<<"NO"<<'n';
	}
	return 0;
}

T2 数(Number)

【题目描述】

给定正整数n,m，问有多少个正整数满足：
(1)不含前导0；
(2)是m的倍数；
(3)可以通过重排列各个数位得到n。

【输入数据】

一行两个整数n，m。

【输出数据】

一行一个整数表示答案对998244353取模的结果。

【样例输入】

1 1

【样例输出】

1

【数据范围】

对于20%的数据，n<10^10。
对于50%的数据，n<10^16，m<=20。
对于100%的数据，n<10^20，m<=100。

分析

这道题是个数位dp，稍微有点难想，但经过中国著名艺术家歌唱家最懂得运用说话艺术周tx的点拨，我好歹是弄懂了一点皮毛。那么接下来让我们来慢慢分析。(也许接下来的的分析还是会有点瑕疵，请大佬轻踩555)
首先关于我们选择进制的问题，我们不能选择二进制进行状压，因为数据范围比较大。
我们用一个数组来存储n中每个数字出现的次数，并定义一个k[], p[]。
让我们举个栗子：
n = 5520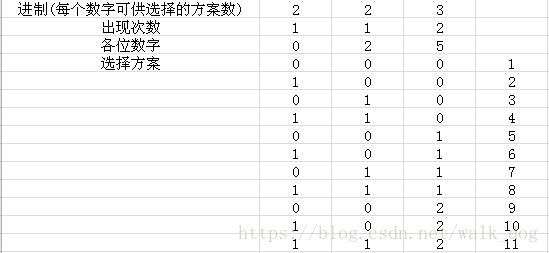

我们可以看出0这个数，逢2进1, 2这个数，逢4进1, 5这个数，逢12进1(未在图中标出，没有第12种情况)，于是我们设k[i]表示第i个数逢几进1，并在这里把它称作这个数的进制，不难发现k[i] = k[i-1] * a[b[i]]。
再来看p[]数组，我们设的是，当前第i个数，需要几次才能加1。不难发现p[i] = k[i-1]。
那么这个时候这个题已经解决了一半了。
接下来我们看看怎么设状态和怎么转移。
我们设f[i][j]表示当前在状态i，我们已经拼成的数%m=j时满足条件的数量。我们设一个now，设当前我们在状态6吧， 我们要判断每个数在这个状态里出现了几次，就找到一个位置，使得 p[i]<=now<=p[i+1],于是我们可以知道i这个数，一定出现了，我们怎么判断前面的数就用now-p[i]即可(看表)，补充一个求i出现了几次的方法，用now/p[i]。
接下来我们来看状态转移方程：
f[i][(x10+b[j])%m] = (f[i][(x10+b[j])%m] + f[i-p[j]][x]) % MOD
x代表已经找到的数，我们在后面加一个数y，自然有10*x+y。
这道题就到这里就结束了，是不是很简单啦啦啦？

//code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

typedef long long  ll;
const int MOD = 998244353;
const int MAXN = 100;
int m, f[60000][105];//jun zhi bu deng shi
char n;
//char n[MAXN];
int a[MAXN], b[MAXN], k[MAXN], p[MAXN];


int main()
{
	while(n = getchar())
	{
		if(n<'0' || n >'9') break;
		a[n-'0']++;
	}
	cin >> m;
//	scanf("%s%d", n+1, &m);
//	for(int i = 1; i <= strlen(n); i++) a[n[i]-'0']++;
	int Len = 0;
	for(int i = 0; i <= 9; i++) 
		if(a[i]) b[++Len] = i;
	if(Len==1 && !b[Len])
	{
		printf("1");
		return 0;
	}
	k[0] = 1;
	for(int i = 1; i <= Len; i++)
	{
		k[i] = k[i-1] * (a[b[i]]+1);
		p[i] = k[i-1];
	}
	f[0][0] = 1;
	for(int i = 1; i < k[Len]; i++)
	{
		int now = i;
		for(int j = Len; j >= 1; j--)
		{
			if(now >= p[j])
			{
				if(!b[j] && i<=k[j])
					continue;
				for(int x = 0; x < m; x++)
				{
					f[i][(x*10+b[j])%m] = (f[i][(x*10+b[j])%m] + f[i-p[j]][x]) % MOD;
				}
				now %= p[j];
			}
		}
		
	}
	printf("%d", f[k[Len]-1][0] % MOD);
	return 0;
}

T3 木门道伏击战intercept

【题目背景】

建兴九年（231 年）， 诸葛亮率蜀军四出祁山。 司马懿料到蜀军粮草不济，坚守
不出，又命人在成都散布诸葛亮欲谋反的谣言。刘禅听信谣言，下旨命诸葛亮退
兵。在退兵时，魏军决定追击，诸葛亮早有防备，在木门道伏击射杀张郃。

【题目描述】

小 W 在《三国演义》中读到四出祁山，对此非常感兴趣，在思考这场战役时 他想出了一个问题。 小 W 认为蜀军共有 N 处伏击地点，可以把这 N 个伏击地点从 1 到 N 进行标 号，且蜀军恰好有 M 个兵种。 由于伏击需要保证军队可以方便地调度，所以不 存在连续 M 个伏击地点埋伏了 M 个不同的兵种。小 W 想知道所有不同的埋伏 方案数对 1e9+7 取模。

【输入格式】

从文件中intercept.in读入数据。
一行一个数 N。

【输出格式】

输出到文件 intercept.out 中。
一行一个数，表示结果对 1e9+7 取模的结果。

【样例输入 1】

3 3

【样例输出 1】

21

【数据范围】 对于 8%的数据， m=2

对于另 16%的数据， n<=10,m<=4
对于 48%的数据， n<=100000,m<=10
对于 80%的数据， n<=100000,2<=m<=100
对于 100%的数据， 2<=m<=100,m<=n<=10^16

分析

这道题是一道蛮简单的dp题，100分做法要用矩阵优化，所以我就只做了80分做法，也挺不错的。
我们设f[i][j]表示走到第i个点，使用了j种不同的军队的方案数。
得到状态转移方程
f[i+1][j+1] += (m-j) * f[i][j]
for(int k = 1; k <= j; k++)f[i+1][j]+=f[i][j]
这里不再解释这两个方程如何得出，请读者自行证明

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;

typedef long long  ll;
const int MAXN = 1e5+5;
const ll MOD = 1e9+7;
ll m, n, Ans;
ll f[MAXN][105];

int main()
{
	scanf("%lld%lld", &n, &m);
	f[1][1] = m;
	for(int i = 1; i <= n; i++)
	{
		for(int j = 1; j <= m; j++)
		{
			if(j+1 < m) f[i+1][j+1] = (f[i+1][j+1] + (m-j)*f[i][j]) % MOD;
			for(int k = 1; k <= j; k++)
				f[i+1][k] = (f[i+1][k]+f[i][j]) % MOD;
		}
	}
	for(int i = 1; i < m; i++)
		Ans = (Ans + f[n][i]) % MOD;
	printf("%lld", Ans);
	return 0;
}