【题解】模拟赛11.22 T4 星际战争

首先想想暴力做法
先以1为起点跑一遍$bfs$
枚举每个除1以外的点作为基地，跑一遍$bfs$统计答案
复杂度为$O(n^2)$，可以拿到20分的好成绩

然后第二部分的$bfs$可以优化， 当前如果跑到一个已经不可能保护的点，就是路径长大于和1的距离，就不必再继续跑下去了，结果就过了80分

然后是一棵树的部分，还是先以1为起点，建树建好
考虑对于一个非1的点$x$，可以保护哪些点

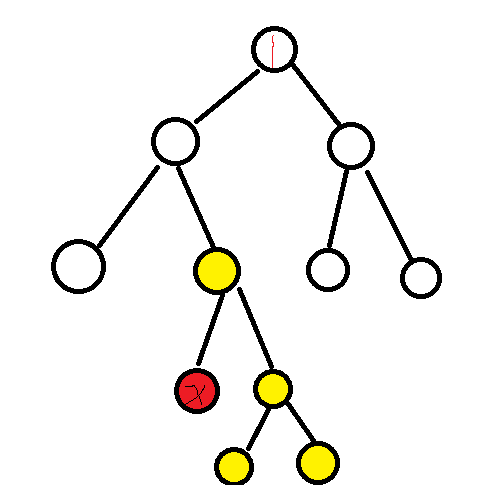
令$dis[x][y]$表示两点最短距离
$F(x,p)$表示从$x$往上走$p$步到达的祖先
对于一个点$x$，$p=\lfloor \frac{dis[1][x]}{2}\rfloor$
它能保护以$F(x,p)$为根的子树所有
那么对于树而言，其实就是计算1的儿子中，谁的子树最大

至于基环树的部分，在一棵树的基础上多了一条边
其实这是一个启发点

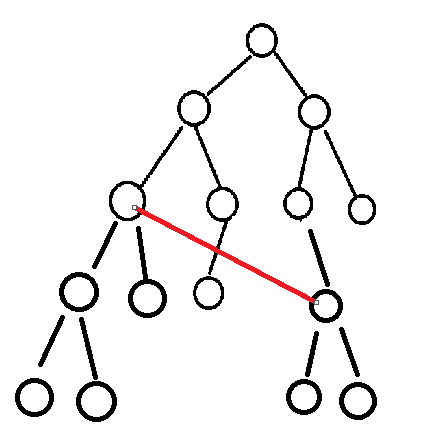
首先我们希望保证，对于原树而言，1到任何点的路径仍然是最短路
那么对于多出来的一条边，相当于多了一点变数

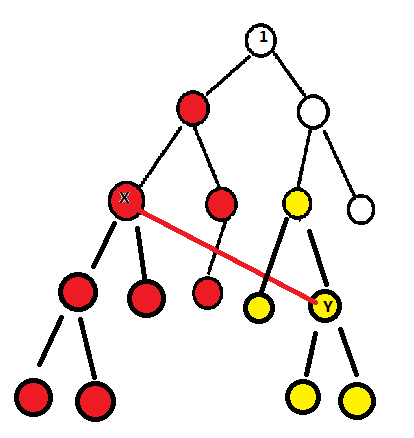
红色是一个点本来就能保护的，黄色是这个点$x$可以通过多出来的这条边保护的点
为什么这条边指向的$y$，是能让$x$多保护一些点的？
发现可以满足$dis[x][y]<=dis[1][y]$
而且$p=\lfloor \frac{dis[1][y]-dis[x][y]}{2}\rfloor$
点$x$可以保护$F(y,p)$的子树

接下来直接思考满分做法
先以1为起点，跑一遍$bfs$，经过的边连成一棵树，这是我们需要的“最短路树”
另外还会多出来$100$条边，相应的最多会多出$200$个点，这些点为特殊点
对于我们枚举的每一个非1的基地$x$，考虑计算这些特殊点对$x$会产生的额外的$贡献$

对于每一个基地$x$
对于每一个特殊点$y$
如果$dis[x][y]<=dis[1][y]$（这部分，是以200个特殊点为起点都跑一遍bfs预处理出来）
$p=\lfloor \frac{dis[1][y]-dis[x][y]}{2}\rfloor$
点$x$可以保护$F(y,p)$的子树（这部分，通过倍增往上跳求得）

发现只要把200个特殊点对于某一个基地额外的贡献计算出，是不会漏掉的，但是会重复
现在想想如何统计到底多少点可以被保护
发现每次都是能保护一棵子树，那么就应用dfs序
每次就是覆盖一个区间，然后把最多200个这样的区间合并，可以直接用布尔数组扫，也可以按照端点排序计算

如果懂了的话就可以自己构思构思代码实现，只用到了bfs，dfs，倍增，快拍等
然后时间复杂度是倍增的复杂度，需要枚举每个点作为基地，枚举200个特殊点，倍增跳点
所以$O(200nlogn)$，差不多要4s是合理的，不过加个火车头就可以2s

Code：

#include <bits/stdc++.h>
#define maxn 100010
using namespace std;
struct Edge{
	int to, next;
}edge[maxn << 1];
struct Block{
	int l, r;
}block[maxn];
int num, head[maxn], vis[maxn], fa[maxn][25], flag[maxn << 1], n, m, special[maxn];
int cnt, node[maxn], dis[220][maxn], d[maxn], dfn[maxn], size[maxn], Index;
int tot, ans, power[25];
queue <int> q;

inline int read(){
	int s = 0, w = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;
	for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);
	return s * w;
}

void addedge(int x, int y){ edge[++num] = (Edge){y, head[x]}, head[x] = num; }

bool cmp(Block x, Block y){
	return x.l == y.l ? x.r < y.r : x.l < y.l;
}

void dfs(int u, int pre){
	d[u] = d[pre] + 1, fa[u][0] = pre, dfn[u] = ++Index, size[u] = 1;
	for (int i = 0; fa[u][i]; ++i) fa[u][i + 1] = fa[fa[u][i]][i];
	for (int i = head[u]; i; i = edge[i].next){
		int v = edge[i].to;
		if (!flag[(i + 1) >> 1]){
			special[u] = special[v] = 1;
			continue;
		}
		if (v == pre) continue;
		dfs(v, u);
		size[u] += size[v];
	}
}

void build(){
	q.push(1);
	vis[1] = 1;
	while (!q.empty()){
		int u = q.front(); q.pop();
		for (int i = head[u]; i; i = edge[i].next){
			int v = edge[i].to;
			if (vis[v]) continue;
			flag[(i + 1) >> 1] = 1, vis[v] = 1;
			q.push(v);
		}
	}
	dfs(1, 0);
}

void bfs(int opt, int st){
	q.push(st), dis[opt][st] = 0;
	for (int i = 1; i <= n; ++i) vis[i] = 0; vis[st] = 1;
	while (!q.empty()){
		int u = q.front(); q.pop();
		for (int i = head[u]; i; i = edge[i].next){
			int v = edge[i].to;
			if (vis[v]) continue;
			dis[opt][v] = dis[opt][u] + 1, vis[v] = 1;
			q.push(v);
		}
	}
}

int find(int u, int goal){
	for (int i = 20; i >= 0; --i)
		if (goal >= power[i]) goal -= power[i], u = fa[u][i];
	return u;
}

void solve(int base){
	int goal = (d[base] - d[1]) >> 1;
	int u = find(base, goal);
	tot = 1, block[tot].l = dfn[u], block[tot].r = dfn[u] + size[u] - 1;
	for (int i = 1; i <= cnt; ++i){
		u = node[i];
		if (dis[i][base] > dis[i][1]) continue;
		int goal = (dis[i][1] - dis[i][base]) >> 1;
		int v = find(u, goal);
		++tot;
		block[tot].l = dfn[v], block[tot].r = dfn[v] + size[v] - 1;
	}
	sort(block + 1, block + tot + 1, cmp);
	int lst = 0, sum = 0;
	for (int i = 1; i <= tot; ++i){
		if (block[i].l > lst) sum += block[i].r - block[i].l + 1, lst = block[i].r;
		else if (block[i].r > lst) sum += block[i].r - lst, lst = block[i].r;
	}
	ans = max(ans, sum);
}

int main(){
	n = read(), m = read();
	power[0] = 1;
	for (int i = 1; i <= 20; ++i) power[i] = power[i - 1] << 1;
	for (int i = 1; i <= m; ++i){
		int x = read(), y = read();
		addedge(x, y), addedge(y, x);
	}
	build();
	for (int i = 2; i <= n; ++i)
		if (special[i]){
			node[++cnt] = i;
			bfs(cnt, i);
		}
	
	for (int i = 2; i <= n; ++i) solve(i);
	printf("%dn", n - ans);
	return 0;
}

最后

以上就是幸福水蜜桃为你收集整理的【题解】模拟赛11.22 T4 星际战争的全部内容，希望文章能够帮你解决【题解】模拟赛11.22 T4 星际战争所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。