一. 简介
离散傅里叶变换(Discrete Fourier Transform,缩写为DFT),是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作其周期延拓的变换。
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
x
p
(
−
j
2
π
N
n
k
)
X(k)=sum_{n=0}^{N-1}x(n)exp(-jfrac{2pi}{N}nk)
X(k)=n=0∑N−1x(n)exp(−jN2πnk)
在c语言中,一个复数是有浮点类型表示的实部和虚部,这可以借助欧拉公式计算
e
i
x
=
c
o
s
x
+
i
(
s
i
n
x
)
e^{ix}=cosx+i (sinx)
eix=cosx+i(sinx)
二. 用C语言实现
取 x(n) =[0,1,2,3],对其进行DFT运算,代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.1415926
int N ; //定于序列长度变量
double Input_Squence[100]; //输入的原始数据序列
double Ampl[100] ; //存储幅值计算结果
typedef struct //定义复数结构,下面通过欧拉公式运算
{
double real,imag;
}complex;
complex Result_Point[100];
void DFT_Calculate_Point(int k)
{
int n = 0;
complex Sum_Point;
complex One_Point[N];
Sum_Point.real = 0;
Sum_Point.imag = 0;
for(n=0; n<N; n++)
{
One_Point[n].real = cos(2*PI/N*k*n)*Input_Squence[n]; //复数的实部
One_Point[n].imag = -sin(2*PI/N*k*n)*Input_Squence[n]; //复数的虚部
Sum_Point.real += One_Point[n].real; //对实部求和
Sum_Point.imag += One_Point[n].imag; //对虚部求和
}
Result_Point[k].real = Sum_Point.real;
Result_Point[k].imag = Sum_Point.imag;
}
void DFT_Calculate()
{
int i = 0;
for(i=0; i<N; i++)
{
DFT_Calculate_Point(i);
Ampl[i] = sqrt(Result_Point[i].real * Result_Point[i].real + Result_Point[i].imag * Result_Point[i].imag); //计算幅值
}
}
int main(int argc, char *argv[])
{
N = atoi(argv[1]); //atoi,将字符串转换为整数值。
//argv[ ],用来存放指向你的字符串参数的指针
int i = 0;
for(i=0; i<N; i++)//产生输入序列
{
Input_Squence[i] = i;
}
DFT_Calculate(); //进行DFT计算
for(i=0; i<N; i++)
{
printf("%dt%lfn",i,Ampl[i]); //输出计算结果
}
return 0;
}
运行结果:
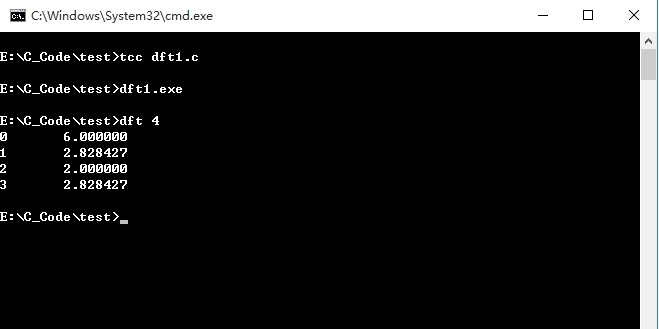
用gnuplot画出图形:
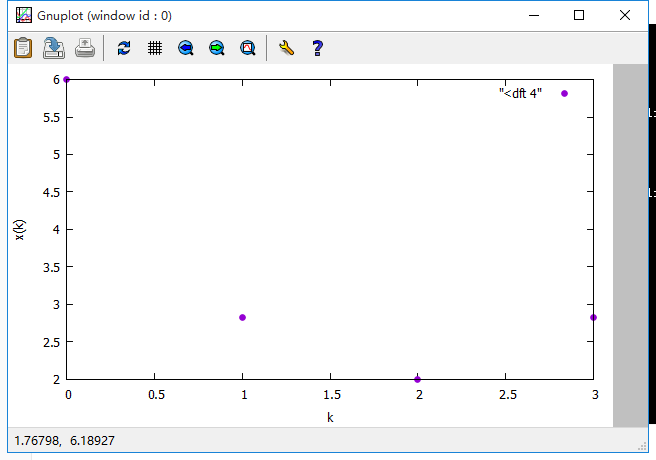
三. 用MATLAB实现
代码:
clear all;
N=4;
x=[0, 1,2,3];%输入信号
a=zeros(1,N);b=zeros(1,N);%构造长度为N的序列
for k=0:N-1
for i=0:N-1
a(k+1)=a(k+1)+x(i+1)*cos(2*pi*k*i/N);%DFT公式
b(k+1)=b(k+1)+x(i+1)*sin(2*pi*k*i/N);
end
c(k+1)=sqrt(a(k+1)^2+b(k+1)^2);%算出幅值
end
f=(0:1:N-1);
plot(f,c,'r*'); %画图
title('DFT');xlabel('k');ylabel('x(k)');
运行结果:
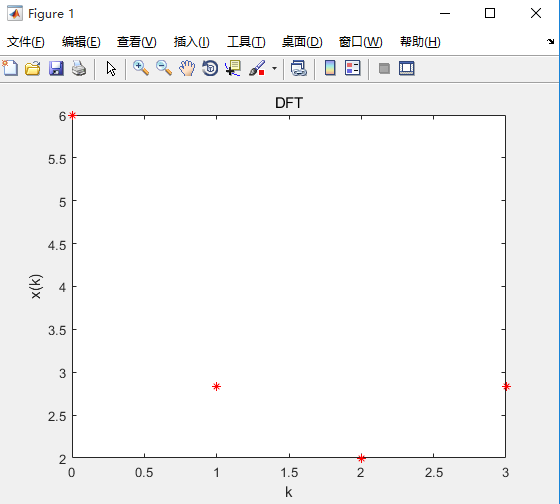
通过比较,发现与用C语言所画图基本一致,对比二者数值:
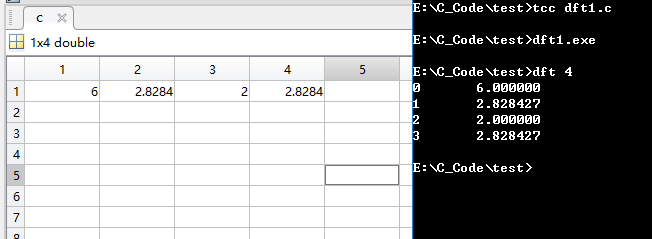
最后
以上就是包容羽毛最近收集整理的关于用C语言实现DFT算法的全部内容,更多相关用C语言实现DFT算法内容请搜索靠谱客的其他文章。








发表评论 取消回复