第一部分基础算法（第四章深度优先搜索）例题

57 阅读 0 评论 38 点赞

我是靠谱客的博主聪慧未来，最近开发中收集的这篇文章主要介绍第一部分基础算法（第四章深度优先搜索）例题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

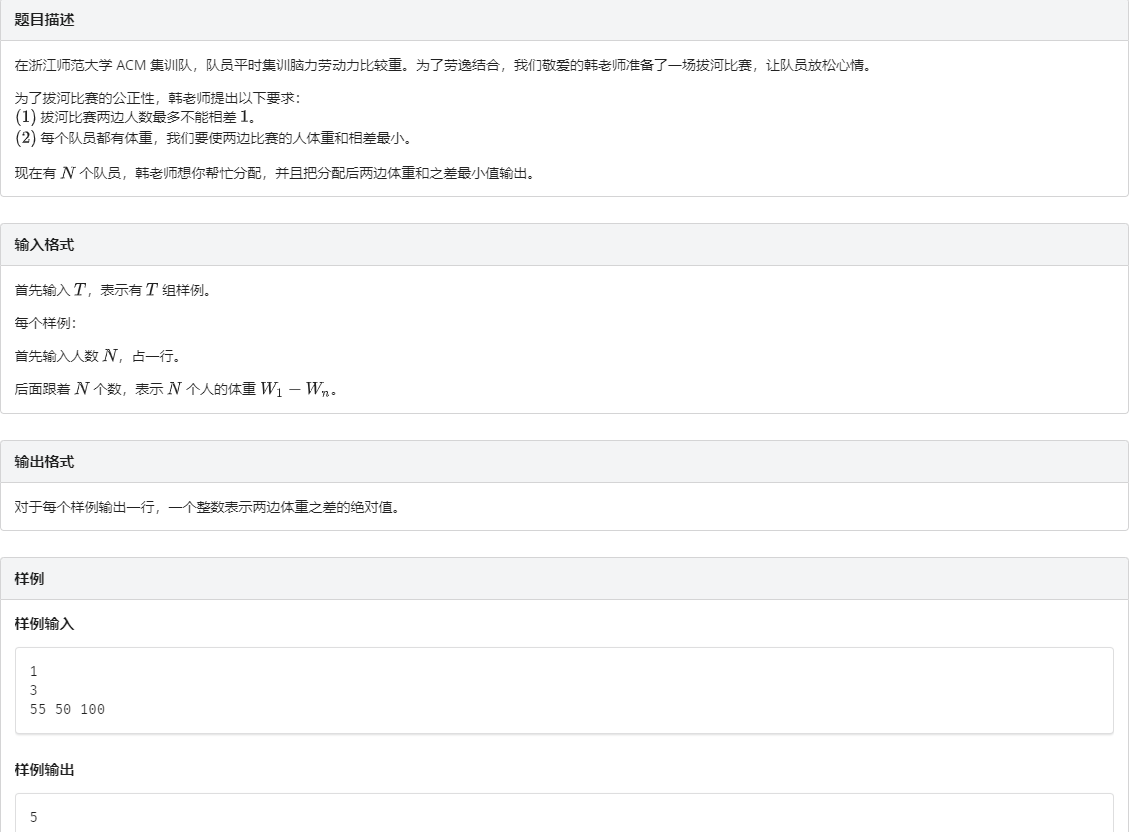
例题一：拔河比赛 link

在这里插入图片描述

思路：
考虑条件（1）,显然只用构造一个大小为n/2的组

考虑条件（2），显然两个组的体重之和是固定的，
记所有人的体重和为S,
则我们只用考虑构造出来的每一个的体重和尽可能接近S/2即可。

通过dfs函数来完成以上操作，
有一个三元组（x,y,z）描述当前状态（第x位成员，已选y个人，体重和为z）

#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
const int N = 30;
const int MAX = 1 << 31 - 1;
int t, n, w[N], ans, sum;
void dfs(int x, int y, int z)
{
	if(y == n / 2) {ans = min(ans, abs(sum - 2 * z)); return ;}
	if(x > n) return ;
	dfs(x + 1, y + 1, z + w[x]);
	dfs(x + 1, y, z);
}
int main()
{
	scanf("%d", &t);
	while(t--)
	{
		scanf("%d", &n), ans = MAX, sum = 0;
		for(int i = 1; i <= n; i++) scanf("%d", &w[i]), sum += w[i];
		dfs(1, 0, 0);
		printf("%dn", ans);
	}
	return 0;
}

例题二：数独游戏 link

在这里插入图片描述
判断重复
数独要求每一行、每一列、每一个3×3方阵内的数字，不重复。

行和列重复判断是相当简单的。我们可以定义两个bool型二维数组，当此行（或列）填充数字时，我们可以直接把这行的这个数字打上true表示有数字了。

//譬如第一行第三列填入数字2
bool p[][],l[][];//p:行,l:列;
p[1][2]=l[3][2]=true;

如果后面再填充数字，就判断此行（或列）是否填过这个数字即可。

重点：判断方阵中数字重复
如果判断方阵中数字重复？怎样用行列来表示是几方阵成了个问题。但是不用怕，我们有van能的数学。

观察下面这个数独：
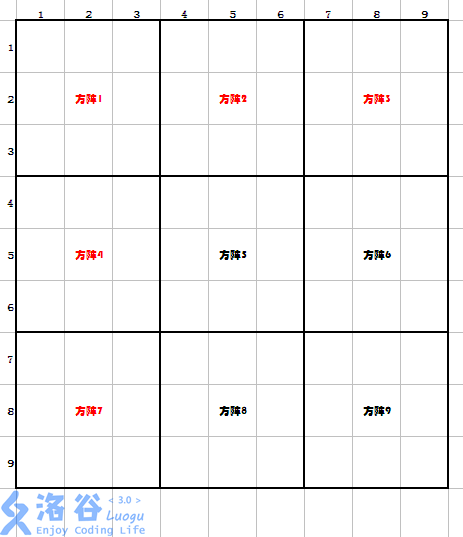
在这里插入图片描述
可以看到，每过3列，方阵的序号+1，每过3行，方阵的序号+3。

于是我们有了这样的表达式：

方阵序号=（行数-1）/3*3+（列数-1）/3+1
//注意！行数列数要-1，因为3的整数倍数/3会比原方阵大1，不能满足上述需求。

有了上述方法，就可以写个深搜函数来解决问题了！

#include <cstdio> 
#include <iostream> 
#include <cstdlib>
using namespace std;
const int N = 15;
int ans[N][N], t;
bool h[N][N], l[N][N], g[N][N];
int solve(int x, int y) {return (x - 1) / 3 * 3 + (y - 1) / 3 + 1;}
void print()
{
	for(int i = 1; i <= 9; i++)
	{
		for(int j = 1; j <= 9; j++)	
			printf("%d ", ans[i][j]);
		printf("n");
	}
	exit(0);
}
void dfs(int x, int y)
{
	if(ans[x][y])
		if(x == 9 && y == 9) print();
		else if(y == 9) dfs(x + 1, 1);
		else dfs(x, y + 1);
	else
	{
		for(int i = 1; i <= 9; i++)
		{
			if(!h[x][i] && !l[y][i] && !g[solve(x, y)][i]) 
			{
				ans[x][y] = i, h[x][i] = l[y][i] = g[solve(x, y)][i] = 1;
				if(x == 9 && y == 9) print();
				else if(y == 9) dfs(x + 1, 1);
				else dfs(x, y + 1);
				ans[x][y] = 0, h[x][i] = l[y][i] = g[solve(x, y)][i] = 0;
			}
		}
	}
}
int main()
{
	for(int i = 1; i <= 9; i++)
	 for(int j = 1; j <= 9; j++)
	 {
		scanf("%d", &t);
		if(t) h[i][t] = l[j][t] = g[solve(i, j)][t] = 1, ans[i][j] = t;
	 }
	dfs(1, 1);
	return 0;
}

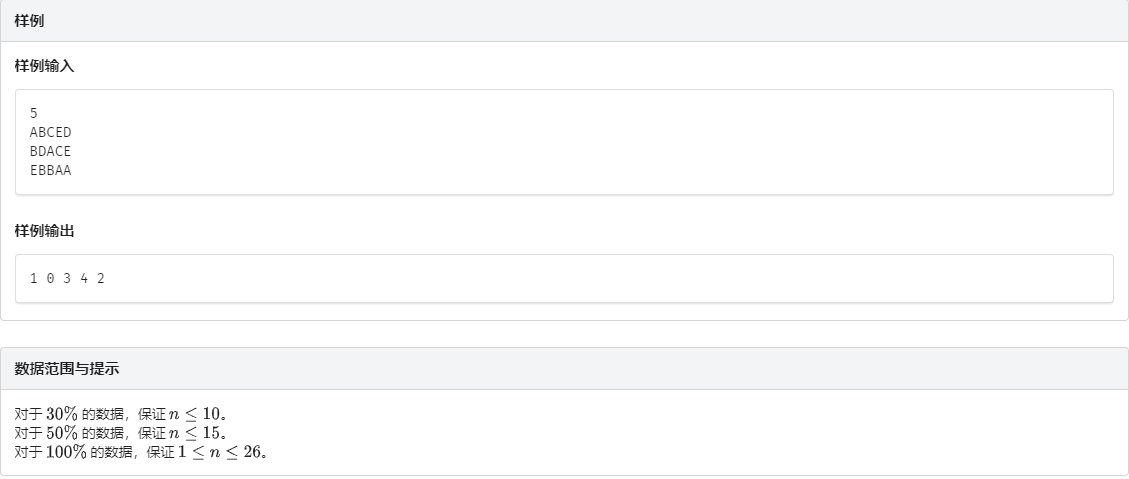
例题三：虫食算 link

在这里插入图片描述

思路：

这道题我们显然是不能去枚举N个字母所代表的数，
不然时间复杂度就会升华到O（N!）。

依次枚举每一个字母代表哪个数
手动做竖式加法是从右往左，这样方便下面的剪枝：

从右往左枚举每一列，记当前加数，被加数，
和分别为a, b, c,如果右边的数已经全部赋值，
则当前的进位我们也是知道的，记为t
如果 $a + b + t \neq = c$ ,那么方案不合法
如果右边存在某一个未知数尚未确定，则进位t可能去0或1，
那么如果 $a + b + 0 \neq = c$ && $a + b + 1 \neq = c$ ,那么方案不合法
另外对于最高位，由题意得是不可能进位的，
即当i==1时，判断是有进位，有进位则方案不合法

#include <cstdio>
#include <iostream>
#include <cstring> 
using namespace std;
const int N = 27; 
int n, cnt[N], tot, a, b, c, num[N];
bool vis[N], used[N];
char s[N][N];
bool check()
{
	int x = 0;
	for(int i = n; i >= 1; i--)
	{		
		a = num[s[1][i] - 'A'];
		b = num[s[2][i] - 'A'];
		c = num[s[3][i] - 'A'];
		if(a != -1 && b != -1 && c != -1)
		{
			if(x != -1)
			{
				if((a + b + x) % n != c) return 0;
				if(i == 1 && a + b + x >= n) return 0;
				x = (a + b + x) / n; 
			}
			else
			{
				if((a + b + 0) % n != c && (a + b + 1) % n != c) return 0;
				if(i == 1 && a + b >= n) return 0;
			}
		}
		else x = -1;
	}
	return 1;
}
bool dfs(int x)
{
	if(x == tot + 1) return 1;
	for(int  i = 0; i < n; i++)
		if(!used[i])
		{
			num[cnt[x] - 'A'] = i; used[i] = 1;
			if(check() && dfs(x + 1)) return 1;
			num[cnt[x] - 'A'] = -1; used[i] = 0;
		}
	return 0;
}
int main()
{
	memset(num, -1, sizeof(num)); 
	scanf("%d", &n);
	for(int i = 1; i <= 3; i++) scanf("%s", s[i] + 1);
	for(int j = n; j >= 1; j--)
	 for(int i = 1; i <= 3; i++)
	  if(!vis[s[i][j] - 'A'])
		vis[s[i][j] - 'A'] = 1, cnt[++tot] = s[i][j];
	dfs(1);
	for(int i = 0; i < n; i++) printf("%d ", num[i]);
	return 0;
}