从小白的角度理解二项分布、几何分布和泊松分布

        先说一下背景，无意间解出来《吴军的数学讲义》这本书，看到概率论的部分有点疑惑，加上当年概率论基本没去上课，于是自己上网研究了半天，终于算是搞明白了其中的区别，下面就从一个近似数学小白的角度说一下各种分布的使用场景。

二项分布：

二项分布的特点：

1、做某事的次数是固定的，用n表示

2、每一次事件都有两个可能的结果（成功或者失败）

3、每一次成功的概率都是相等的，成功的概率用p表示

4、你感兴趣的是成功x次的概率是多少

比如，你每次买彩票只有中与不中两种概率，假设中的概率是10%（当然没这么高），你想知道，如果我买100次彩票，我能中多少次。那么就用二项分布：

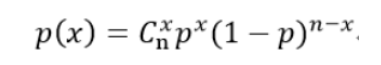
 几何分布：

1、做某事的次数是固定的，用n表示

2、每一次事件都有两个可能的结果（成功或者失败）

3、每一次成功的概率都是相等的，成功的概率用p表示

4、你感兴趣的是进行x次尝试，取得第一次成功的概率是多少

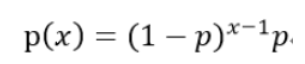
 跟上面的二项分布很像，区别是你想知道的结果不一样了，你想知道我买10次彩票必定有一次成功的概率是多少。有人会说100%，因为中奖率是10%，但是现实并不是每10你一定会中奖，因此用几何分布来算。

泊松分布：

1、事件是独立的

2、在任意相同的时间范围内，事件发生的概率相同

3、你想知道某个时间范围内，发生某时间x的概率是多大

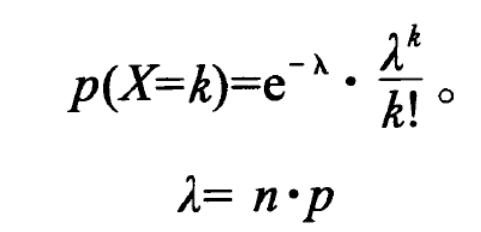
泊松分布是对一段时间或者空间发生事件的概率进行计算的一种方法，即已知群体样本的平均值，求部分样本的值是多少的时候用泊松分布 。听起来貌似不太好理解，举个例子，一个培养皿有100ml的培养液，平均每ml有10个细菌，那么取出1ml的培养液，里面恰好有n个细菌的概率是多少，这时候用泊松分布。

从公式上来看，二项分布和几何分布用到了n（几何分布中是x），不同的是二项分布想知道能成功多少次，几何分布想知道这么多次能成一次的概率有多大（让我想起了DNF的武器强化）。而泊松分布没有用到n，即具体样本为多大（注意这里的λ=n*p是指平均值，可能通过统计学直接得到平均值λ），用来计算某一段时间内发生某事k次的概率。

高斯分布：

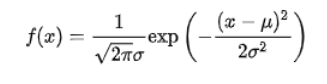
顺便提一嘴高斯分布，大样本数据在知道方差和期望的情况下一般都认为近似服从高斯分布。可以在通过统计数据进行建模时使用高斯分布。

总结：都是数学工具，使用场景不一样，不必要纠结其中的数学联系，作为一种工具，只需要知道什么时候使用哪种工具更方便就可以了。

最后

以上就是迷你魔镜为你收集整理的从小白的角度理解二项分布、几何分布和泊松分布的全部内容，希望文章能够帮你解决从小白的角度理解二项分布、几何分布和泊松分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。