2021 ICPC第二场网络赛 G题题解

65 阅读 0 评论 43 点赞

我是靠谱客的博主高贵台灯，最近开发中收集的这篇文章主要介绍2021 ICPC第二场网络赛 G题题解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Given 2n integers, a1,a2,…,an,b1,b2,…,bn, and an integer t. You need to calculate:

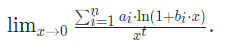
Input

The first line consists of two integers n,t.

In the following n lines, the i-th line consists of two integers ai,bi.

1≤n≤100000,−100≤ai,bi≤100,0≤t≤5.

Output

Please output the result of this limit. If the result is ∞, please output "infinity" (without quotes). And if the result is an integer, please output this integer directly. Otherwise, the answer must be ba, such that a and b are coprime and b≥2, please output "a/b".

题目描述：给出一个极限的式子，让我们计算它的数值

解题思路：首先我们需要知道高阶无穷小和低阶无穷小的情况，对于任意的分母x^t，如果存在x^k(k < x)的情况，那么将会让整个式子无穷大，若存在x ^ k(k > x)的情况，那么式子将会无穷小不受影响，如果不存在无穷大的情况，那么整个式子的结果将会等于分子和分母指数相同时的系数之比

再者我们需要知道ln（x + kx）是能够展开的

然后就用这个方法写就可以了

然后贴一下最终代码

#include <bits/stdc++.h>
using namespace std;
#define FAST std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int n,t;
long long a,b;
long long xs[10];
int main()
{
	FAST
	cin >> n >> t;
	if(t == 0)
	{
		cout <<"0"<<"n";
		return 0;
	}
	for(int i = 1;i <= n;++i)
	{
		cin >> a >> b;
		xs[1] += a * b;
		xs[2] -= a * b * b;
		xs[3] += a * b * b * b;
		xs[4] -= a * b * b * b * b;
		xs[5] += a * b * b * b * b * b;
	}
	for(int i = 1;i < t;++i)
	{
		if(xs[i] != 0)
		{
			cout <<"infinity"<<"n";
			return 0; 
		}
	}
	if(xs[t] % t == 0) cout << xs[t] / t<<"n";
	else cout <<xs[t]<<"\"<<t<<"n";
	return 0;
}