Codeforces Round #360 (Div. 2) -- C. NP-Hard Problem （DFS二分图染色法）

78 阅读 0 评论 52 点赞

我是靠谱客的博主正直电源，最近开发中收集的这篇文章主要介绍Codeforces Round #360 (Div. 2) -- C. NP-Hard Problem （DFS二分图染色法），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Recently, Pari and Arya did some research about NP-Hard problems and they found theminimum vertex cover problem very interesting.

Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edgeuv there is at least one endpoint of it in this set, i.e.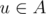 $\text{[math]}$ or $\text{[math]}$ (or both).

Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.

They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A andB, such that bothA andB are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).

Input

The first line of the input contains two integers n andm (2 ≤ n ≤ 100 000,1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.

Each of the next m lines contains a pair of integersu_i andv_i (1 ≤ u_i, v_i ≤ n), denoting an undirected edge betweenu_i andv_i. It's guaranteed the graph won't contain any self-loops or multiple edges.

Output

If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).

If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integerk denoting the number of vertices in that vertex cover, and the second line containsk integers — the indices of vertices. Note that because ofm ≥ 1, vertex cover cannot be empty.

Examples

Input

4 2
1 2
2 3

Output

Input

Output

-1

Note

In the first sample, you can give the vertex number 2 to Arya and vertices numbered1 and3 to Pari and keep vertex number4 for yourself (or give it someone, if you wish).

In the second sample, there is no way to satisfy both Pari and Arya.

大体题意：

给你一个无向图，判断是否能够构成一个二分图，如果能的话，输出二分图左边的集合和右边的集合。

思路：

通过这个题目学习了二分图染色法，静下心来感觉并不难。

先给每一个顶点的color设置为-1，表示没有被染色，用vector数组v[a]，表示元素a所相连的全部元素。

然后枚举每一个顶点，发现没有被染色，就对他进行染色，先把顶点染成0，然后再0颜色的vector加入当前元素，在枚举与这个元素相连的元素，假设颜色是c的话，相连的就染成c^1，这个方法会把0变成1，1变成0，因为二分图氛围左边和右边，就可以这么理解，左边是0，右边是1，在dfs中发现该元素已被染色就return，发现染色的颜色与该染的颜色不符合，就不能构成二分图了，ok=false。

有个小小的剪枝，发现ok已经false了直接return了。这样会快一定的速度。

详细见代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn = 100000 + 10;
vector<int>g[maxn],v[2];
bool ok = true;
int color[maxn];
void dfs(int k,int c){
if(!ok)return;
if (color[k] != -1){
if (color[k] != c)ok=false;
return;
}
color[k] = c;
v[c].push_back(k);
int len = g[k].size();
for (int i = 0; i < len; ++i)dfs(g[k][i],c^1); // 0 -> 1,, 1 -> 0;
}
void print(vector<int> & t){
int len = t.size();
printf("%dn",len);
for (int i = 0; i < len; ++i){
if (i)printf(" ");
printf("%d",t[i]);
}
printf("n");
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for (int i = 0; i < m; ++i){
int u,w;
scanf("%d%d",&u,&w);
g[u].push_back(w);
g[w].push_back(u);
}
memset(color,-1,sizeof color);
for (int i = 1; i <= n; ++i){
if (color[i] == -1)dfs(i,0);
}
if (!ok)printf("-1n");
else {
for (int i = 0; i < 2; ++i)print(v[i]);
}
return 0;
}