1 题目

蜜蜂寻路
时间限制 1000 ms 内存限制 32768 KB 代码长度限制 100 KB 判断程序 Standard (来自 小小)
题目描述
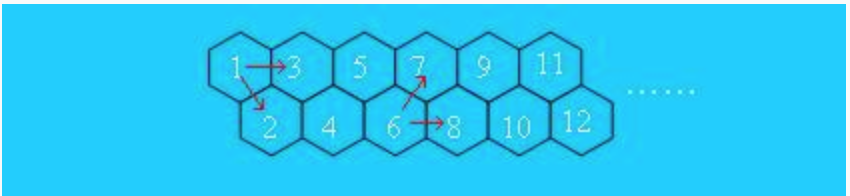
nowcoder利用业余时间养了一窝蜜蜂，因为空间比较小，蜂房只有两排，如下图所示：

如你所见，蜜蜂的蜂房是正六边形，假设蜜蜂只会从左往右爬，即从1号蜂房能爬到2号和3号；从6号蜂房能爬到7号和8号……

现给出两个蜂房的编号a和b，要求计算蜂房a的蜜蜂爬到蜂房b有几条不同路线。

输入描述:

1. 输入的第一行是一个整数n
2. 接下来n行数据，每行一组测试用例
3. 每组测试用例包含两个正整数a和b，(0 < a < b < 2^31)

输出描述:
每组用例的结果单独输出一行。输出数据结果范围是 [0, 2^63)。

输入例子:
3
1 2
3 6
99 100

输出例子:
1
3
1

2 解析

设n为b与a的差值，F(n)为从a到b的方案。
由题目的图知$F(1)=1,F(2)=2$,下面开始递推讨论
当n为3时：

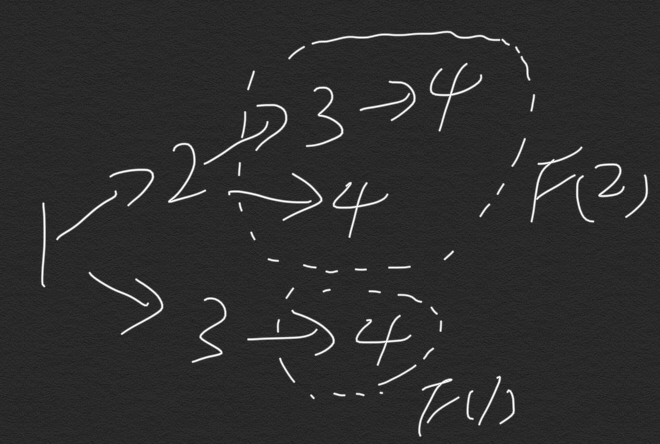
当n为4时：

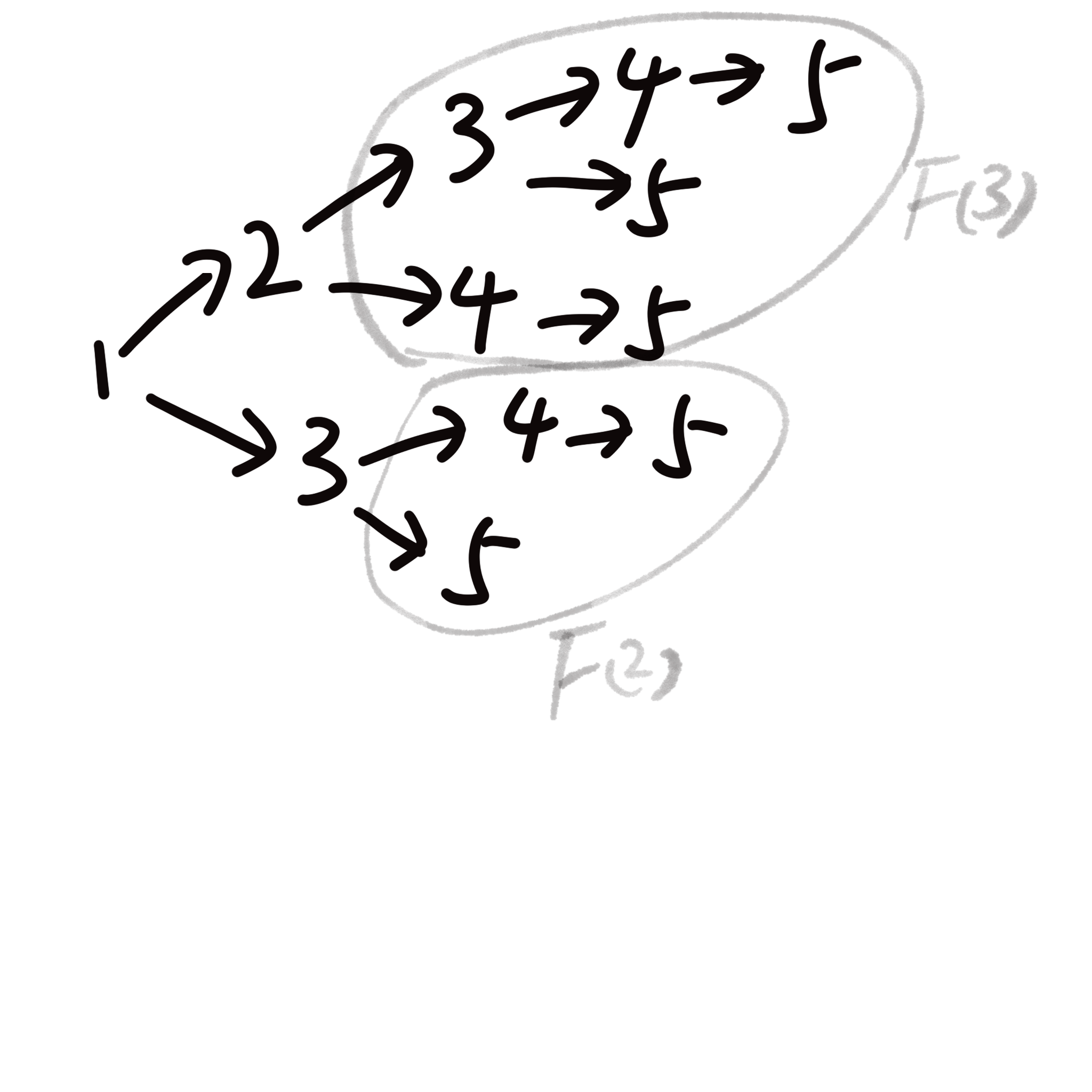
依次递推，得到递推公式：F(n) = F(n-1) + F(n-2).
也就是斐波那契数列。
由动态规划的知识：
递推式子：
$F(n)=F(n-1)+F(n-2)$
递推边界：
$F(1)=1,F(2)=2$
从递推边界出发，依次递推便可得到整个递推式。

3 参考代码

#include <cstdio>

typedef long long ll;
const int MAXN = 100010;
ll f[MAXN] = {1,1,2};

int main(int argc, char const *argv[]){
    int n, a, b;
    for (int i = 3; i < MAXN; ++i) {
        f[i] = f[i -1] + f[i -2];//递推式
    }
    scanf("%d", &n);
    while(n--){
        scanf("%d%d", &a, &b);
        printf("%lldn", f[b - a]);
    }
    return 0;
}

最后

以上就是开心秋天为你收集整理的蜜蜂寻路————动态规划（递推）1 题目2 解析3 参考代码的全部内容，希望文章能够帮你解决蜜蜂寻路————动态规划（递推）1 题目2 解析3 参考代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。